Приклад:

1. ρ = 1,00013 г/см³, цей результат можна записати:г/см³.

2. ρ = 0,99973 г/см³, можна записатиг/см³.

Коли не можна відкидати або додавати числа, а це відноситься до констант табличних даних, тоді записують як половина числа відомого розряду після коми:

.

3. Обчислення похибок при посередніх вимірах. У більшості випадків фізичні величини залежать функціонально одна від одної, а деколи від декількох величин. При цьому користуються формулами диференціювання, так як формули похибок одержують в тому приближенні, що і формули для диференціалу функції. Для находження абсолютної похибки користуються готовими формулами, які представлені в таблиці.

Таблиця

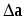
Математична операція a	Абсолютна похибка	Відносна похибка Ea
x + y
x–y
xy
xyz
xn	nxn–1
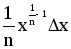
lnx
sinx	cosx	ctgx
cosx	sinx	tgx
tgx
ctgx

Якщо математична формула складна тоді необхідно:

• прологарифмувати новий диференціал функції;

• найти новий диференціал функції;

• обчислити абсолютну похибку, замінив знак диференціалу dна знак абсолютної похибки;

• обчислити відносну похибку E_x;

• записати результати обчислень.

Приклад:

Модуль Юнга кістки обчислюється за формулою: ,

де:

F– сила навантаження;

f – стріла прогину;

l, b, h– лінійні розміри кістки.

Для обчислення абсолютної похибки використовуємо формули диференціювання:

1. lnE = lnF + 3lnl – ln3,2 – lnf – lnb – 3lnh.

2. .

3. .

4. .

5. E_x=.

Величини: – обчислюємо, використовуючи лабораторний або технічний метод обчислення абсолютних похибок.