Задачи для самостоятельного решения

21. Сколькими способами можно распределить между тремя людьми 3n различных предметов так, чтобы каждый получил предметов?

22. Сколькими способами можно разложить т+п+р различных предметов на три группы так, чтобы в первой группе было т, во второй п, и в третьей р предметов?

23. Сколькими способами можно разделить 12 различных марок между 3 мальчиками, если каждый берет по 4 марки?

24. Сколькими способами можно разделить 12 различных марок между 3 мальчиками, если один берет 6 марок, а остальные − по 3 марки?

В рассмотренных ранее примерах ящики были различимыми. Но это не всегда так. Рассмотрим некоторые примеры.

Задача. Из 60 различных белых грибов хотят сделать 4 связки по 15 грибов в каждой. Сколькими способами это можно сделать?

Решение. На первый взгляд эта задача относится к разобранному выше типу и имеет ответ Но здесь есть одна тонкость. При разделе костей домино важно, кому из игроков достанется данный набор костей, а при составлении связок грибов порядок связок роли не играет − в кладовой все они будут висеть вместе. Поэтому ответ надо еще разделить на 4! − число перестановок связок между собой. Поэтому здесь ответ:

Вообще, если надо разделить тр различных предметов на т групп по р предметов в каждой группе, причем порядок групп не учитывается, то число способов раздела равно

Более общей является такая задача: п различных элементов надо распределить на т групп так, чтобы тгрупп содержали по рэлементов, тгрупп содержали по рэлементов,…, тгрупп содержали по рэлементов (и ).

Сколькими способами может быть произведен раздел, если

а) группы различимы; б) группы неразличимы, (например, предметы кладутся в одинаковые ящики, которые потом перемешиваются)?

В первом случае ответ имеет вид:

А во втором случае надо иметь в виду возможность перестановки групп, содержащих поровну элементов. Теперь уже ответ иной:

25. Даны 2п элементов. Рассматриваются всевозможные разбиения этих элементов на пары, причем разбиения, отличающиеся друг от друга только порядком элементов внутри пар и порядком расположения пар, считаются совпадающими. Сколько существует различных таких разбиений?

26. Сколькими способами можно из 30 рабочих создать 3 бригады по 10 человек в каждой бригаде?

27. Сколькими способами можно разложить 10 книг на 6 бандеролей по 2 книги в каждой (порядок бандеролей не принимается во внимание)?

Формула включений и исключений

Пусть имеется N предметов, каждый из которых может обладать свойствами а,а,...,а.При этом каждый предмет может обладать одним или несколькими свойствами, а может не обладать ни одним из этих свойств.

Обозначим через N(аа…а)количество предметов, обладающих свойствами а,а,...,а(и, быть может, еще некоторыми из других свойств). Если нам надо будет отметить, что берутся лишь предметы, не обладающие некоторым свойством, то это свойство пишем с чертой сверху. Например, через N()обозначено количество предметов, обладающих свойствами и , но не обладающих свойством (вопрос об остальных свойствах остается открытым).

Число предметов, не обладающих ни одним из указанных свойств, Обозначают по этому правилу через N(…).Общий закон состоит в том, что

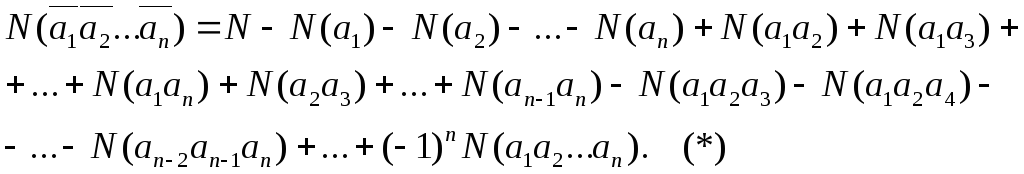
Здесь алгебраическая сумма распространена на все комбинации свойств а,а,...,а(без учета их порядка), причем если число учитываемых свойств четно, то ставится знак «+», а если это число нечетно, то ставится знак «−».

Например, входит со знаком «+», а − со знаком «−». Формулу (*) называют формулой включений и исключений − сначала исключаются все предметы, обладающие хотя бы одним из свойств а,а,...,а,потом включаются предметы, обладающие, по крайней мере, двумя из этих свойств, исключаются имеющие по крайней мере три из этих свойств, и т. д.