Перестановки с повторениями
Определение. Перестановкой с повторениями из m элементов состава k1, k2,…,km называют кортеж длины суммы k1+k2+…+km, где k1 – число повторений одного элемента множества, k2 – число повторений другого элемента множества и т.д., km – количество повторений оставшегося элемента множества.
Обозначают:
.
Теорема
10. Число
различных перестановок с повторениями
данного состава (n1,
n
,
...,n
)
вычисляют по формуле
,
где
n
=n1
+n
+...+
nт.
Рассмотрим
одну перестановку и заменим в ней все
одинаковые элементы разными. Тогда
число различных перестановок, которые
можно составить из рассматриваемой
нами перестановки, по правилу произведения
равно n1,
n
,...,
n
.
Проделав это для каждой перестановки,
получим n!
перестановок.
Следовательно,
∙n1!∙n2∙…∙nm!
= n!.
Теорема доказана.
Задача. Сколькими способами можно расставить белые фигуры: 2 коня, 2 слона, 2 ладьи, ферзя и короля на первой линии шахматной доски?
Решение. В этой задаче надо найти число кортежей длины 8, имеющих заданный состав (2, 2, 2, 1, 1). Число таких кортежей, то есть перестановок с повторениями, равно 5040.
.
Ответ: 5 040 способами.
Общую задачу о перестановках с повторениями можно сформулировать следующим образом: имеются предметы m различных типов. Сколько перестановок можно сделать, взяв n1 элементов первого типа, n2 типа, ..., nm элементов m-го типа?
Задача. Сколько различных буквенных комбинаций (не обязательно имеющих смысл) можно получить, переставляя буквы слова «кишмиш»?
Решение. В данном слове одна буква «к», две буквы «и», две буквы «ш», одна буква «м», всего 1+2+2+1=6 (букв).
Значит,
Р(1,2,2,1)=
(слов).
Ответ: 180 слов.
Задачи для самостоятельного решения
Сколько слов, состоящих из восьми букв, можно образовать из 6 букв алфавита?
В магазине имеется 7 видов тетрадей в клеточку. Сколькими способами можно купить 12 тетрадей?
Сколькими способами можно расставить белые фигуры: два коня, две ладьи, ферзя и четыре пешки – на одной линии шахматной доски?
Сколько будет костей геометрического домино, если использовать в их образовании следующие геометрические фигуры: квадрат, треугольник, круг, ромб?
Сколько различных буквенных комбинаций (не обязательно имеющих смысл) можно получить, переставляя буквы слова «комбинаторика»? Переставляя буквы слова «математика»?
Сколькими способами можно обить 12 стульев, если имеется 5 сортов обивочного материала?
Бином Ньютона
В алгебре довольно часто приходится возводить в степень двучлен (a+b). Недаром каждый школьник заучивает наизусть формулы квадрата и куба суммы двух чисел. Аналогичная формула, но уже для произвольного натурального числа п≥1 называютбиномом Ньютона, хотя и была известна задолго до того времени, когда жил Ньютон. Слово «бином» в переводе с латыни означает «двучлен».
Теорема 11. Для любого целого неотрицательного n справедливо тождество:
.
Левая
часть равенства является произведением
n
одинаковых сомножителей:
.
Если раскрыть скобки, не приводя подобных
и не группируя одинаковые сомножители
в степени, получится сумма, в которой
каждое слагаемое является произведениемn переменных,
по одной из каждого сомножителя. Например,
.
Каждое
слагаемое в этой сумме имеет вид слова
в алфавите {x,y},
в котором i–тую
позицию занимает переменная, выбираемая
из i–того
сомножителя. Нетрудно видеть, что каждое
слово длины n
появится в этом выражении в точности
один раз. После группировки сомножителей
каждое слово, в котором буква x
встречается k
раз, превращается в слагаемое вида
.
Таких слов имеется ровноC
,
поэтому после приведения подобных
получается правая часть равенства.
Ранее были приведены следующие свойства биномиальных коэффициентов:
1)
;
4)
;
2)
;
5)
;
3)
;
6)
.
Особенно
важным свойством является последнее.
Оно позволяет с помощью одних только
операций сложения найти все числа
сочетаний из n
элементов,
если известны числа сочетаний из (
)
элемента. Это же свойство лежит в основе
построения таблицы биномиальных
коэффициентов, называемой треугольником
Паскаля.
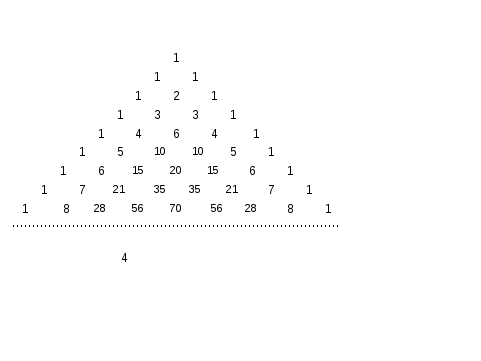
Треугольник Паскаля является, пожалуй, одной из наиболее известных и изящных числовых схем во всей математике. Блез Паскаль, французский математик и философ, посвятил ей специальный «Трактат об арифметическом треугольнике». Впрочем, эта треугольная таблица была известна задолго до 1665 года – даты выхода в свет трактата.
Так, в 1529 году треугольник Паскаля был воспроизведен на титульном листе учебника арифметики, написанного астрономом Петром Апианом.
Изображен треугольник и на иллюстрации книги «Яшмовое зеркало четырех элементов» китайского математика Чжу Шицзе, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника в 1110 году, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
В треугольнике Паскаля биномиальные коэффициенты располагаются следующим образом:
C
. . . . . . . . .
В
этой бесконечной таблице строка с
номером n
(n=0,1,2,...)
образована числами C
,
k
пробегает все значения от 0 до n.
При этом каждая следующая строчка
сдвинута относительно предыдущей таким
образом, что непосредственно над числом
C
левее и правее его оказываются расположены
числа
и
,
сумма которых, по свойству 6), как раз и
равнаC
.
Таким образом, если строка с номером
(
)
заполнена, то легко заполняется строка
с номером n:
первый и последний элементы всегда
равны 1, а каждый из остальных получается
сложением двух расположенных над ним
элементов предыдущей строки.
В треугольнике Паскаля прослеживаются следующие закономерности.
1. Члены всякой строки треугольника Паскаля сначала возрастают (до середины строки), а затем − убывают.
Например, 1<4<6, 6>4>1 (четвертая строка); 1<5<10, 10>5>1 (пятая строка).
2. Всякая строка треугольника Паскаля симметрична относительно своей середины (то есть члены всякой строки треугольника Паскаля, равноудаленные от ее краев, равны между собой).
Формально
это свойство записывается в виде
упоминавшегося нами равенства
.
3.
Сумма
членов n-й
строки треугольника Паскаля равна 2
.
То
есть
.Это
можно рассматривать как следствие
формулы бинома Ньютона,
если положить
.Важно,
однако, разобраться в теоретико-множественной
интерпретации данного свойства. Число
равно
количеству m-элементных
подмножеств n-элементного
множества. Поэтому левую часть формулы
бинома Ньютона можно рассматривать как
число всех подмножеств n-элементного
множества (включая пустое подмножество
и само n-элементное
множество).
4. Всякое непустое множество имеет столько подмножеств с четным числом элементов, сколько и подмножеств с нечетным числом элементов; иными словами, при n≤1
C
+ C
+ C
+ …=C
+ C
+ C
+ …
Данное соотношение получается применением формулы бинома Ньютона к левой части тождества (1 – 1)п=0.
С помощью утверждения 3 можно конкретизировать:
C
+ C
+ C
+ … = C
+ C
+ C
+ …=2
.
Приведем комбинаторное доказательство этого утверждения.
С каждым подмножеством X данного непустого множества
А={а1, а2, ... , ап} свяжем подмножество Y, определяемое следующим образом: Y получается из X путем исключения или, наоборот, путем добавления к нему элемента аi в зависимости от того, содержит X элемент аi или не содержит.
Все подмножества множества А можно таким образом разбить на пары подмножеств (X, У), причем в каждой такой паре одно из подмножеств содержит четное, а другое – нечетное число элементов. Следовательно, подмножеств с четным числом элементов столько же, сколько и подмножеств с нечетным числом элементов.
5. Крайние члены треугольника Паскаля равны 1. Каждый же из остальных членов равен сумме двух смежных с ним членов, стоящих в предыдущей строке.
Например (см. строку с номером п=4),
4=1 + 3; 6=3 + 3; 4=3 + 1.
В
общем случае (при 1≤m≤п)
C
=C
+ C
.
Последняя формула интересна и тем, что несет в себе правило построения каждой последующей строки треугольника Паскаля по предыдущей строке.
Доказать
это равенство можно непосредственными
вычислениями с помощью формулы
.
Однако гораздо
интересней обратиться к ее комбинаторной
трактовке: тех сочетаний из элементов
{ а1,
а2,
... , ап,
an+1}
по т,
которые не
содержат ап+1,
будет, очевидно, С
;
тех же сочетаний, которые содержатan+1,
будет C
.
6.
.
Это
получается при
.
7.
.
Получается
применением формул
и
.
Рассмотрим примеры использования формулы бинома.
Пример.
Разложить
по формуле бинома Ньютона двучлен
Решение.
Пример.
Разложить
по формуле бинома Ньютона двучлен
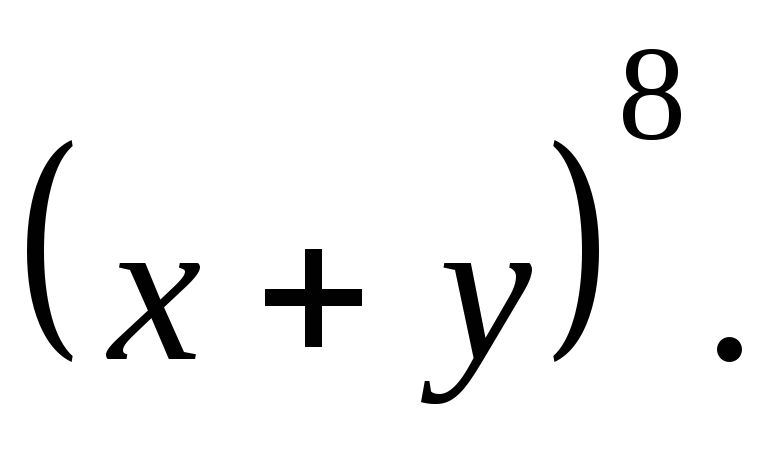
Решение.
Пример.
Запишите
формулу Бинома Ньютона для (х–2у)
.
=
.
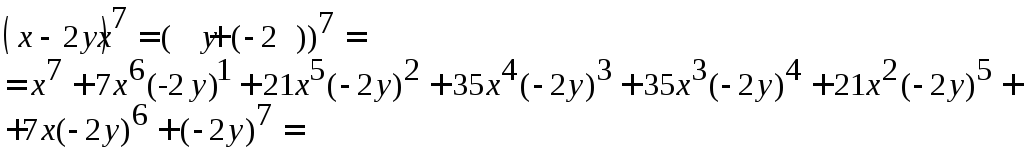