
- •Содержание
- •Понятие комбинаторной задачи
- •История возникновения и развития комбинаторики
- •Конечные множества
- •Операции над множествами
- •Декартово произведение множеств а и в
- •Задачи для самостоятельного решения
- •Нахождение числа всех подмножеств данного множества
- •Понятие факториала
- •Задания для самостоятельного решения
- •Правила суммы и произведения
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Виды соединений без повторений
- •Перестановки без повторений
- •Задачи для самостоятельного решения
- •Размещения без повторений
- •Задачи для самостоятельного решения
- •Сочетания без повторений
- •Свойства чисел c
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Виды соединений с повторениями Сочетания и размещения с повторениями
- •Перестановки с повторениями
- •Задачи для самостоятельного решения
- •Бином Ньютона
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Контрольные вопросы
- •Примеры решения некоторых комбинаторных задач
- •Задачи для самостоятельного решения
- •Примеры решения некоторых комбинаторных задач
- •Задачи для самостоятельного решения
- •Примеры решения некоторых комбинаторных задач
- •Задачи для самостоятельного решения
- •Примеры решения некоторых комбинаторных задач
- •Задачи для самостоятельного решения
- •Формула включений и исключений
- •Примеры решения некоторых комбинаторных задач
- •Задачи для самостоятельного решения по курсу «Комбинаторика»
Вопросы для самопроверки
Что называют «перестановками из п элементов»?
Докажите, что число различных перестановок из n элементов равно произведению последовательных натуральных чисел от 1 до n включительно.
Что называют размещением из n элементов по k?
Как найти число различных размещений из n элементов по k элементов?
Докажите, что А
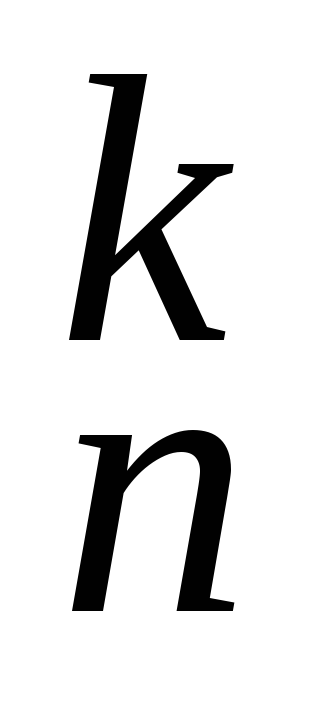 = n
∙ (n
– 1) ∙ (n
– 2) ∙ … ∙ (n
– k
+ 1).
= n
∙ (n
– 1) ∙ (n
– 2) ∙ … ∙ (n
– k
+ 1).Докажите, что А
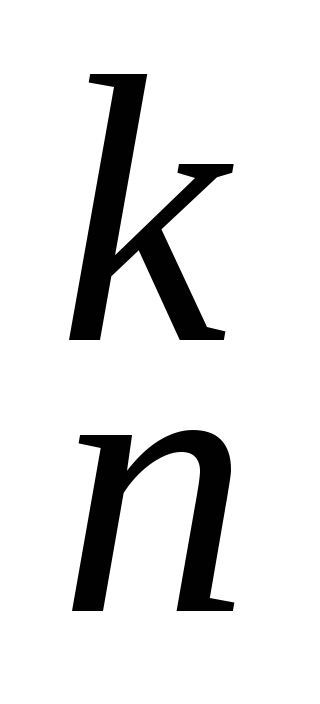 =
=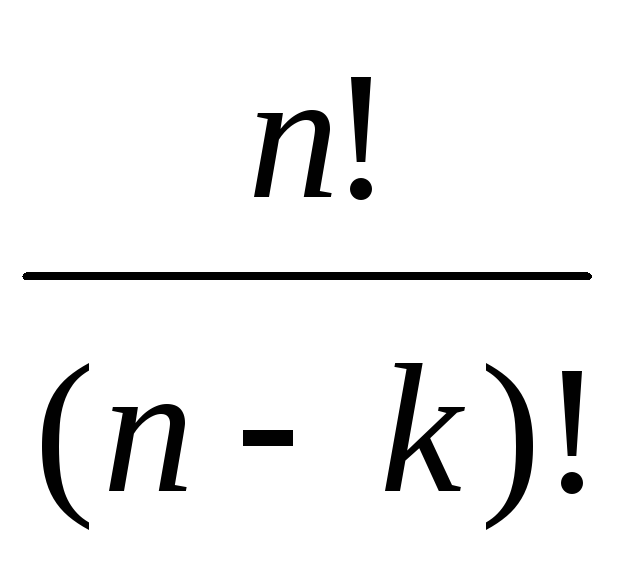 .
.Решите уравнение:
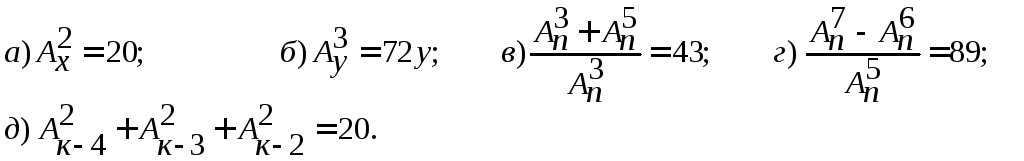
Что называют«сочетанием из n элементов по k элементов»?
Как найти число сочетаний из n элементов по k элементов?
Докажите, что число сочетаний из n элементов по k элементов определяется по формуле C
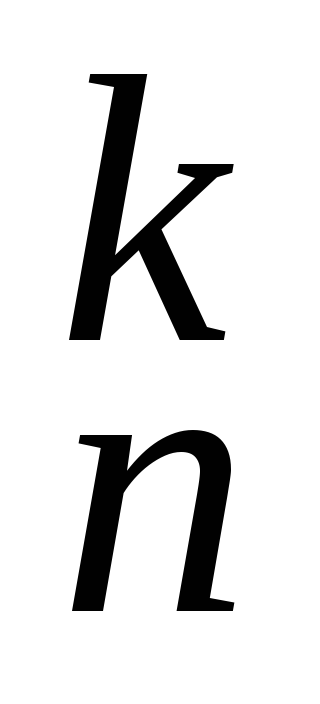 =
=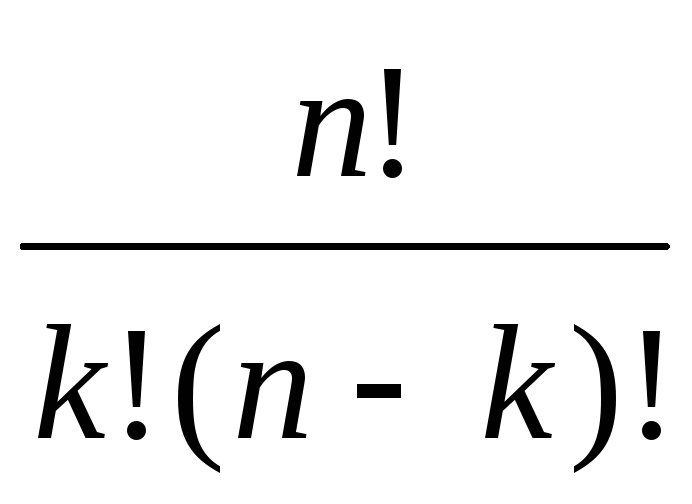 .
.Сколько подмножеств имеет 5-элементное множество?
Сколько трехэлементных упорядоченных подмножеств можно составить из элементов пятиэлементного множества?
Сколько 5-элементных подмножеств можно составить из элементов 5-элементного множества?
Сколько трехэлементных подмножеств можно составить из элементов пятиэлементного множества?
Сколько подмножеств можно составить из элементов трехэлементного множества?
Решите уравнение:
![]()
![]() ;
;
![]() ;
;
![]()
Какие свойства чисел C
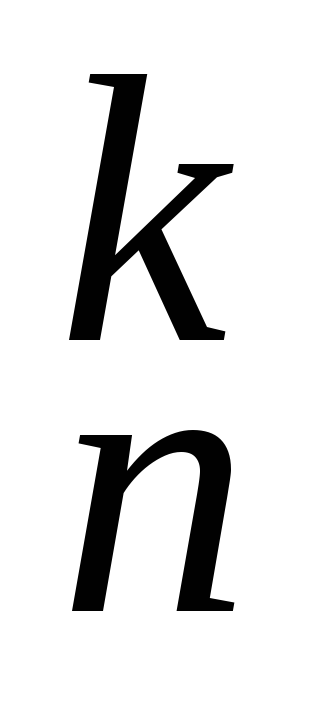 вы знаете?
вы знаете?Докажите, что
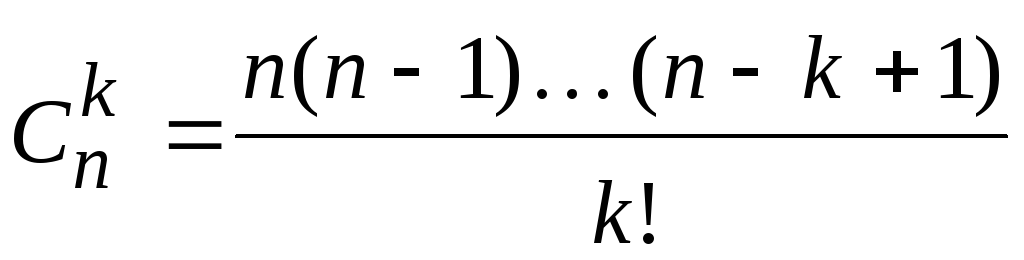 .
.Докажите, что
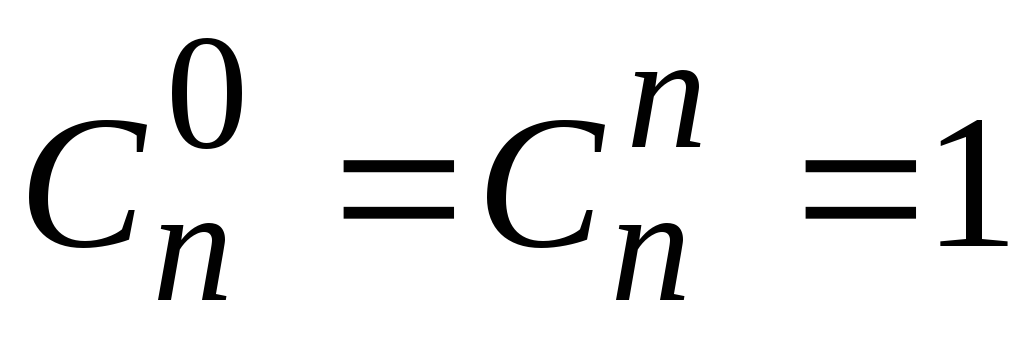 .
.Докажите, что
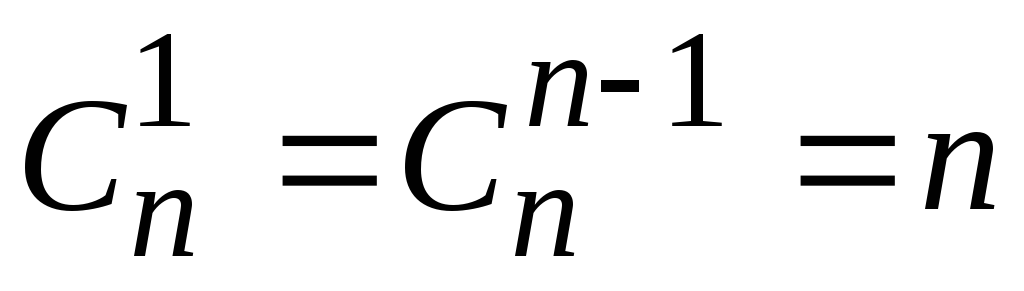 .
.Докажите, что
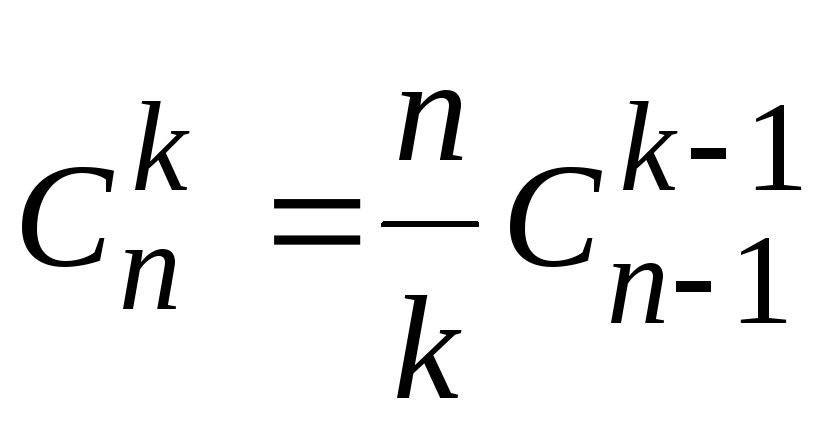 .
.Докажите правило симметрии.
Докажите, что для
 k,n:
0
k,n:
0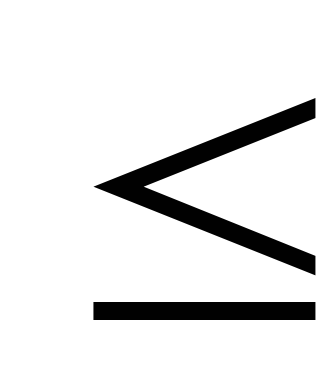 k
k n,
верно равенство:
n,
верно равенство:
(n
+ 1) C![]() =(k
+ 1) C
=(k
+ 1) C![]()
Докажите правило Паскаля.
Докажите, что для любого m верны равенства:
а)
C![]() + C
+ C![]() + … + C
+ … + C![]() =2
=2![]() ;
;
б)
C![]() – C
– C![]() + C
+ C![]() – C
– C![]() +… + (– 1)
+… + (– 1)![]() C
C![]() + … + (– 1)
+ … + (– 1)![]() C
C![]() =0;
=0;
в)
C![]() + C
+ C![]() + C
+ C![]() + … = C
+ … = C![]() + C
+ C![]() + C
+ C![]() + …=2
+ …=2![]() .
.
Докажите, что для любого m верны равенства:
а)
C![]() + C
+ C![]() + C
+ C![]() =С
=С![]() ;
;
б)
C![]() + C
+ C![]() + C
+ C![]() +
+
![]() =С
=С![]() .
.
Виды соединений с повторениями Сочетания и размещения с повторениями
В задачах по комбинаторике могут встретиться множества, в которых какие-либо компоненты повторяются. Например, в задачах о составлении числа из заданных цифр – цифры могут повторяться. Например, используя цифры 7, 4 и 5, можно образовать различные двузначные числа: 77, 74, 75, 47, 44, 45, 57, 54, 55. В записи этих чисел цифры повторяются.
С теоретико-множественной точки зрения запись любого двузначного числа – это кортеж длины 2. Записывая различные двузначные числа с помощью цифр 7, 4 и 5, мы по сути дела образовывали из данных 3 цифр различные кортежи длины 2 с повторяющимися элементами. В комбинаторике такие кортежи называют размещениями с повторениями из 3 элементов по 2.
Определение.Размещением
с повторениями
из k
элементов по m
элементов называют кортеж, составленный
из m
элементов k-элементного
множества. Число всевозможных размещений
с повторениями из k
элементов по m
элементов обозначают
![]() .
.
Из определения следует, что два размещения из k элементов по m элементов отличаются друг от друга либо составом элементов, либо порядком их расположения.
Например, два двузначных числа из перечисленных выше отличаются друг от друга либо составом элементов (77 и 75), либо порядком их расположения (74 и 47).
Относительно размещений часто возникает вопрос: «Сколько всевозможных размещений по m элементов каждое можно образовать из k элементов данного множества?»
Теорема 7. Число
всевозможных размещений с повторениями
из k
элементов
по m
элементов
подсчитывают по формуле:
![]() .
.
Доказательство
проведем
методом математической индукции по k,
где
k
– число
элементов в размещении при фиксированном
значении т.
Прежде всего заметим, что размещения с
повторениями по k
элементов
могут быть получены из размещений по
(k–1)
элементу присоединением еще одного
элемента. Так как к каждому размещению
по (k–1)
элементу можно присоединить любой из
имеющихся т
элементов,
то каждое размещение по (k–1)
элементу порождает т
различных
размещений по k
элементов,
то есть
![]() .
.
1.
При k
= 1
каждое размещение состоит только из
одного элемента, а число элементов равно
т,
значит,
и число размещений равно т.
Итак,
![]() ,
что
соответствует формуле.
,
что
соответствует формуле.
2.
Допустим, что для некоторого числа k
равенство
![]() справедливо.
справедливо.
3.
Найдем число размещений с повторениями
из т
элементов
по k
+
1. Пользуясь формулой
![]() ,
,
получаем:
![]() =
т∙m
=
т∙m![]() =m
=m![]() .
.
Таким образом, доказываемая формула справедлива для k=1 и из ее справедливости для некоторого k следует и справедливость для (k+1). Теорема. доказана.
С помощью этой
формулы легко подсчитать, например,
сколько двузначных чисел можно записать,
используя цифры 7, 4 и 5. Так как речь идет
о размещениях с повторениями из трех
элементов по два, то
![]() .
.
Задача. Обезьяну посадили за пишущую машинку с 45 клавишами. Определите число попыток, необходимых для того, чтобы обезьяна напечатала первую строку романа Л.Н. Толстого «Анна Каренина», если строка содержит 52 знака?
Решение. В данной задаче имеет значение порядок следования букв. Буквы при этом могут повторяться.
Значит, всего есть
![]() (вариантов)
(вариантов)
Ответ: 4552 вариантов.
Задача. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?
Решение.
Так как
порядок следования цифр в числе
существенен, цифры могут повторяться,
то это размещения с повторениями из 5
элементов по 3, а их число равно
![]() (чисел).
(чисел).
Ответ: 125 чисел.
Задача. Каждый телефонный номер состоит из семи цифр. Сколько всего телефонных номеров, не содержащих других цифр, кроме 2, 3, 5 и 7?
Решение. Эта задача о числе размещений на семи разных позициях семи цифр, выбранных из четырех различных цифр с повторениями каждой из них любое число раз, но не более семи, то есть о кортежах длины 7, составленных из элементов множества А, содержащего 4 элемента.
Поскольку
![]() =
47
= 16 384, то число всех указанных номеров
равно 16 384.
=
47
= 16 384, то число всех указанных номеров
равно 16 384.
Ответ: 16384.
Определение. Набор из к элементов, составленный из повторяющихся элементов m элементного множества, называют сочетанием с повторениями из m по к.
Сочетание с
повторениями из m
элементов по к
обозначают
символом
![]() .
.
Теорема 9. Число всевозможных сочетаний с повторениями из к элементов по m элементов подсчитывают по формуле:
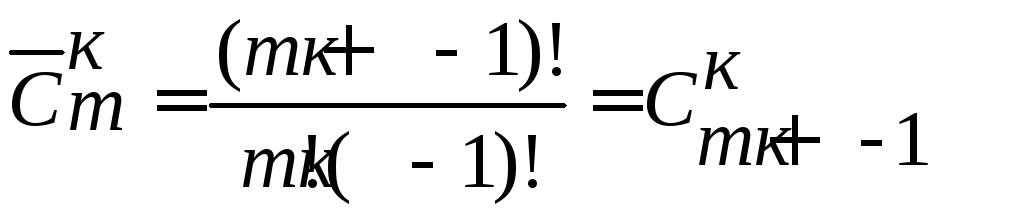 .
.
Фактически нам надо выяснить, сколько различных составов могут иметь кортежи длины к из m элементов. Любой состав кортежа длины к из т элементов имеет вид (к1, к 2, к3,... ,кт), где к1, к2, ..., кm – неотрицательные целые числа, сумма которых равна к. Заменяя каждое из чисел кj (1<j<к) соответствующим количеством единиц и разделяя нулями единицы, отвечающие различным числам, получаем кортеж из (т –1) нулей и к единиц. При этом каждому составу отвечает одна и только одна запись с помощью нулей и единиц, а каждая такая запись задает один и только один состав. Поэтому число различных составов равно числу перестановок с повторениями из (т –1) нулей и к единиц, то есть
![]() =Р(т–1,к)=
=Р(т–1,к)=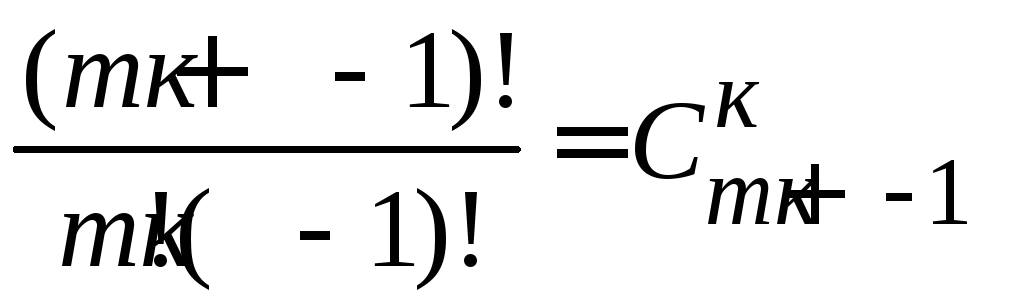 .
.
Теорема доказана.
Задача. В кондитерском магазине продавались четыре сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных?
Решение. Покупка не зависит от того, в каком порядке укладывают купленные пирожные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта. Следовательно, количество различных покупок равно числу сочетаний четырех видов пирожных по семь.
![]() (способов)
(способов)
Ответ: 120 способов.
Задача. Сколько будет костей домино, если использовать в их образовании все цифры?
Решение. Число костей домино можно рассматривать как число сочетаний с повторениями по два из десяти. Число таких сочетаний равно:
![]() =С
=С![]() =
=![]() =55(штук).
=55(штук).
Ответ: 55 костей домино.
