Свойства чисел c
Следующие
простые свойства чисел С
легко выводятся из факториальной формулы
C
=
:
а)
;
б)
;
в)
;
г)
.
д) Правило симметрии.
Если 0
k
n,
то верно равенство: C
=C
.
Известно, что
C
=
.
Найдём C
=
=
=
.
Следовательно,
C
=C
.
Утверждение доказано.
е) Для
k,n:
0
k
n,
верно равенство:
(n
+ 1) C
=(k
+ 1) C
.
(n
+ 1) C
=
=
;
(k
+ 1)C
=
=
=
=
=
.
Следовательно, (n
+ 1) C
=(k
+ 1) C
.
Утверждение доказано.
ж) Правило Паскаля.
k,
n:
0
k
n
верно равенство: C
=C
+ C
.
Найдем C
:
C
=
=
=
;
Найдем C
:
C
=
=
=
.
Найдём C
+ C
:
C
+ C
=
+
=
=
=
=
= C
.
з) Для любого m верны равенства:
C
+ C
+ … + C
=2
;
C
– C
+ C
– C
+…+ (– 1)
C
+ … + (–1)
C
=0;
C
+ C
+ C
+ …=C
+ C
+ C
+ …=2
.
Покажем, как данные свойства можно использовать при решении задач.
Задача 1. Некоторый комитет состоит из 12 человек. Минимальный кворум для принятия решения должен насчитывать 8 человек. а) Сколькими способами может быть достигнут минимальный кворум? б) Сколькими способами может быть достигнут какой-либо кворум?
Решение.
а)
Искомое число совпадает с С
и равно:
С
=С
=С
=
=495
(способа)
б) Какой-либо кворум достигается, если на заседании присутствует 8, 9, 10, 11 или 12 членов комитета. Согласно правилу суммы искомое число равно:
C
+
C
+
C
+
C
+ C
=C
+
C
+
C
+
C
+
C
=
=495 +
+
+
+ 1=794 (способа )
(При вычислении
мы учли, что 0!=1, и поэтому C
=1).
Ответ: а) 495 способов; б) 794 способа.
Задача 2. У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Сколькими способами можно взять выборочный анализ, чтоб изучить течение болезни у 2 взрослых и 3 детей.
Решение. Из 6 взрослых выбрать двух можно:
C
=
=15
(способами)
Из 11 детей выбрать трёх можно:
С
=
=165
(способами)
Согласно правилу произведения имеется 15 ∙ 165=2 475 способов выбора двух взрослых и трёх детей.
Ответ: 2 475 способов.
Задачи для самостоятельного решения
Найдите значение выражения:
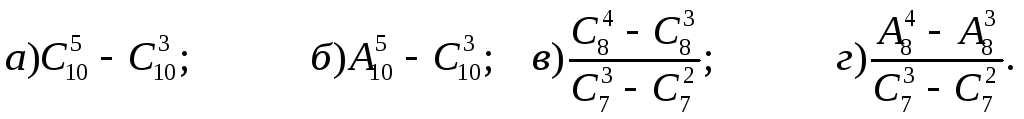
Решите уравнение:
Сколько необходимо взять элементов, чтобы число размещений из них по четыре было в 14 раз больше, чем число размещений из n−2 по три?
Сколькими способами можно выбрать три ленты разных цветов из пяти лент разных цветов?
Сколькими способами можно распределить четыре путёвки в санаторий, между шестью желающими?
Из 10 рабочих нужно выбрать четырех для определённой работы. Сколькими способами можно это сделать?
Сколько различных произведений, содержащих а) два, б) 3, в) 4 сомножителя, можно составить из цифр: 1, 5, 6, 7, 9?
Из состава участников конференции, на которой присутствуют 19 человек, надо избрать делегацию, состоящую из 3 человек. Сколькими способами это можно сделать?
Сколькими способами можно образовать из группы в 12 мужчин и 8 женщин комиссию, так чтобы она состояла из 3 мужчин и 4 женщин?
Из 5 чайных чашек, 6 блюдец и 7 чайных ложек хотят сервировать стол на три персоны, положив каждой из них одну чашку, одно блюдце и одну ложку. Сколькими способами можно это сделать?
Почему 0! = 1?
Сколькими способами можно выбрать 0 объектов из n имеющихся, то есть сколькими способами можно не выбирать ни одного объекта?
Формально имеем:
А
=
=
=1.
Есть только один способ: не выбирать ни одного объекта из n объектов (ничего не делать).
Сколькими способами
можно сделать упорядоченный выбор из
n
объектов всех n?
Р
=n!.
С другой стороны,
это число А
=
=
Найдём 0!
из равенства: Р
= А
,
имеем,
= n!
0! = n!
: n!
= 1
0! = 1.