Свойства счётных множеств:

1⁰ Для того чтобы мн-во А было счётным необходимо и достаточно, чтобы все его элементы могли быть представлены в виде последовательности, т.е. перенумеровать с помощью мн-ва натуральных чисел.

2⁰ Из всякого бесконечного мн-ва можно выделить счётное мн-во.

3⁰ Любое бесконечное подмножество счётного мн-ва также счётно.

4⁰ Объединением конечного числа счётных мн-в явл-ся счётным мн-вом.

5⁰ Объединение счётного мн-ва конечных мн-в также счётно.

6⁰ Объединение счётного мн-ва счётных мн-в также счётно.

7⁰ Если бесконечное мн-во А={a_i,k}, где a_i,k – элементы мн-ва А (i,k),то А счётное мн-во.

8⁰ Мн-во всех рациональных чисел счётно.

Док-во: Q=Q₊Q_{- -нейтр. эл-т} Q₊=, - рац. число (p,q ).

Q₊={a_p,q}- то по св-ву 7 это мн-во счётное Q_- - счётно Q₊Q_- - счётно

Q – счётное мн-во.

Теорема1: Мн-во целых чисел явл-ся счётным мн-вом.

Из бесконечных мн-в нам известно счётное, но существуют другие бесконечные мн-ва – несчётные, н/р, мн-во всех действительных чисел между 0 и 1. Мн-во наз. несчётным, если оно бесконечное, но счётным не явл-ся.

Теорема2: Мн-во действительных чисел на отрезке [0;1] несчётно.

Док-во: (метод от противного)

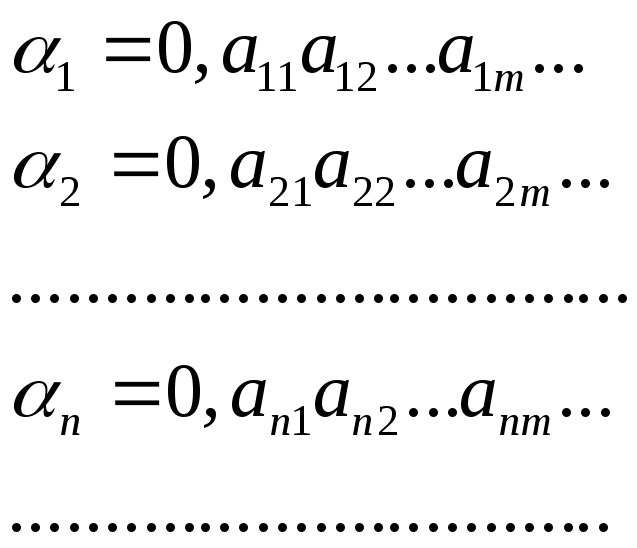Предположим, что мн-во всех R на [0;1] – счётно все элементы этого мн-ва можно перенумеровать с помощью мн-ва всехN чисел.

A=- счётное

Создадим число

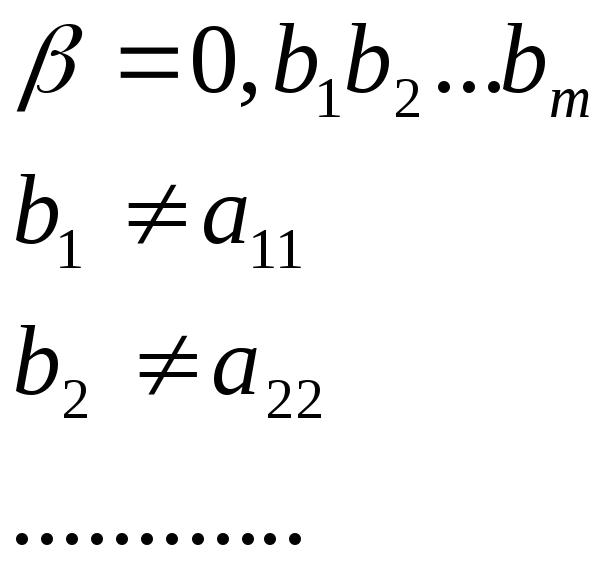(b₁ – любая цифра)

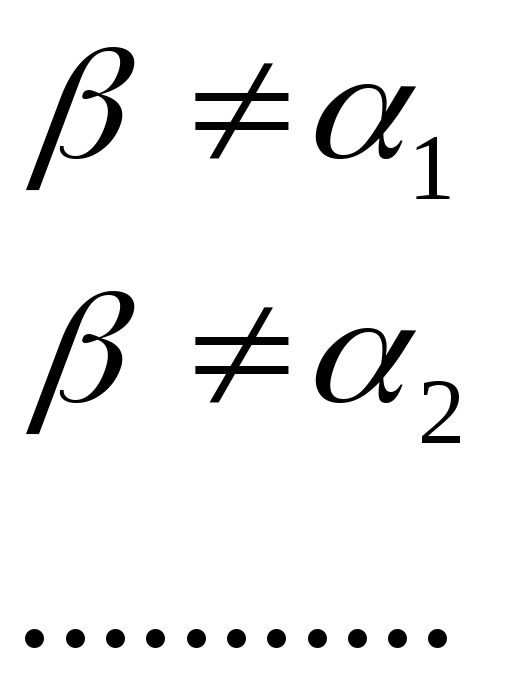
Число не вошло в мн-во А, т.е. предположение было неверным, т.о. мн-во А – счётно

МЕТОДИКА 9.

Изучение рациональных чисел начинается в 6 классе. Понятие о рациональных числах вводится в теме «Положительные и отрицательные числа». И только в 8 классе, вводятся понятия, «дробные выражения», «рациональные дроби», и действие с дробями.

Цели изучения темы

Обучающие цели: - Обеспечить усвоение понятий: положительные и отрицательные числа, противоположные числа, модуль числа, координатная прямая и правила сравнения чисел;

- Научить правильно, воспроизводить термины, определения понятий, приводить примеры;

- Формировать умения записывать и читать положительные и отрицательные числа, противоположные числа, модуль числа, умение сравнивать положительные и отрицательные числа;

- Формировать умения решать типовые арифметические задачи;

Развивающие цели: - Развивать познавательные процессы: внимание, восприятие, память.

- Развивать мышление: умение сравнивать, обобщать, формулировать правила, алгоритмы, делать индуктивные умозаключения;

- Развивать речь, мировоззрение, умение учиться.

Воспитательные цели: - Воспитывать интерес к математике и учебной деятельности через использование исторических и занимательных задач.

- Воспитывать культуру общения, общую культуру.

- Воспитывать отдельные качества личности (настойчивость, трудолюбие).

Урок закрепления

Структура: -Проверка Д\З; - Сообщение темы , цели, мотивация; - Решение задач в стандартных ситуациях; -Применение знаний, в новых, в измененных ситуациях; -Подведение итогов; -Д\З

Цели урока: систематизация и обобщение знаний учащихся по теме;

• развитие логического мышления, аргументированной математической речи;

• повышение интереса к предмету;

• воспитание честности во время взаимоконтроля.

Фрагмент: Тестирование. Проверку осуществляет противоположный вариант и выставляет оценки.

Учащимся раздаются тесты на 2 варианта.

Вариант 1. Какие из равенств верны? а) |3| = 3 ; б) |-3|= 3 ; в) |-3|= -3

2. Верно ли расположены в порядке возрастания числа 0; -5; 3?

3.Чему равно значение выражения -7 + 7? а) 14; в) 0; с) -14; д) нет правильного ответа.

4. Найдите: -27 + 7. а) -36; в) -22; с) 22; д) нет правильного ответа.

5. Найдите: -13 – 47. а) -34; в) 50; с) -50; д) нет правильного ответа.

Критерии оценки.

• “5” - за все правильно выполненные задания;

• “4” - если допущена одна ошибка;

• “3” - если допущено две ошибки;

Примерная методическая схема изучения рациональных дробей в школе.

1вводится понятие дробного выражения и рациональной дроби. (дается определение);2устанавливается правило сокращения дробей и основное свойство дроби;3определяются операции: сложение, вычитание, умножение, деление.В каждой из этих групп выражении изучается их определение, классификация, выделяются выражение стандартного вида или простейшего, изучаются тождественные преобразования.

Основные типы задач.задачи – примеры, в записи условий которых используются только математические символы( цифры, знаки действия, скобки), а словесный текст, как правило отсутствует. Метод их решения – выполнение арифметических действий с учетом правил об их порядке.задачи – расчеты – задачи межпредметного и прикладного характера, иногда с готовой формой расчета. После составления числового выражения приводится к задаче – примеру и решается тем же методом.Текстовые сюжетные задачи более сложного математического характера, которые в большинстве случаев легко решаются алгоритмически, но, если не пользоваться уравнением, представляющие собой некоторые трудности и требующие для решения сообразительности.Стандартные:1) Преобразуйте в дробь выражение.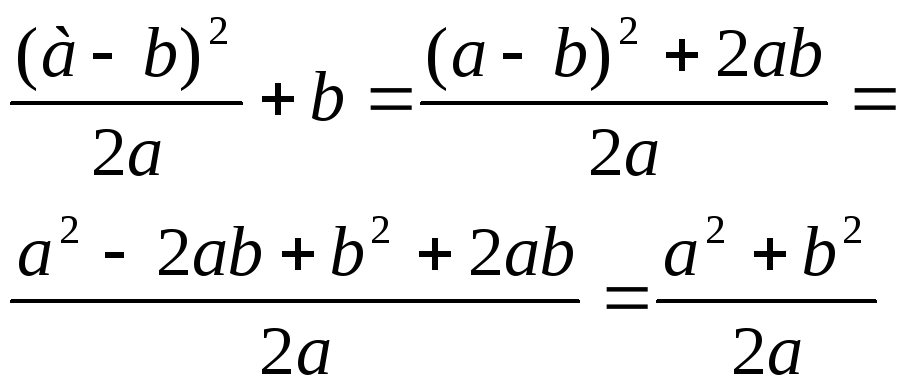Нестандартные:Туристы прошлиs км по шоссе со скоростью v км/ч и вдвое больший путь по проселочной дороге. Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скорость, на 2км/ч меньшей, чем по шоссе?

Билет № 10.«Интеграл».

Пусть дана ф-ция у=f(x) заданная на отрезке [a,b], будем считать, что эта ф-ция непрерывна на нём, тогда F(x) наз. первообразной ф-цией для ф-ции f(x) на отрезке [a,b], если .

(п1) f(x)=х³ F(x)=

Мн-во всех первообразных ф-ции f(x) наз. неопределённым интегралом и обозначается:, гдеf(x) – подынтегральная ф-ция, f(x)dx – подынтегральное выражение, а х – переменная интегрирования.