Матричные уравнения

Рассмотрим матричные уравнения вида:

(1) A  X = B и (2) Y  C = D, где A, C  M_{n n}(F), B  M_{n k}(F), D  M_{k n}(F), причём A, C обратимы, X  M_{n k}(F), Y  M_{k n}(F) – неизвестные матрицы.

Теорема 4.4. (о матричных уравнениях). Матричное уравнение (1) при |A|  0 имеет единственное решение X = A^–1B.

Матричное уравнение (2) при |C|  0 имеет единственное решение

Y = D  C ^–1.

Примеры. 1. Решить уравнение: A  X = B, где А = ,B = .

|A|  0, поэтому решением уравнения будет матрица X = A^–1 B. Вычислим A^–1 с помощью элементарных преобразований:

~ ~ ~

Следовательно, А^-1 = .Х = ·=.

Проверка: ·=.

Ответ: Х = .

2. Решить уравнение: Y C = D, где С = , D = .

|С|  0, поэтому решением уравнения будет матрица Y = D  C ^–1.

Вычислим С ^–1 =  ||С_ij||^t = 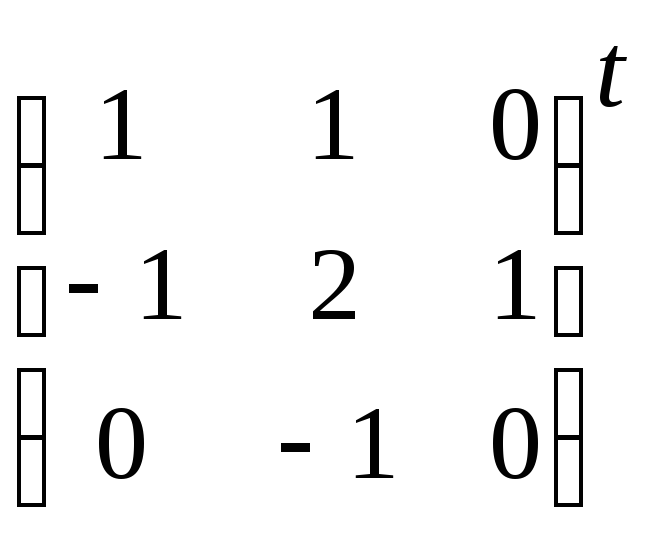 =, Y = D  C ^–1 = =  =.Проверка: ·=.Ответ: Y = .

МЕТОДИКА 14. Тема урока: Решение систем линейных уравнений

Цели урока: знакомство с определением системы линейных уравнений; с определением решения системы; с основными способами решения систем уравнений; развитие навыка применения аналогии при решении задач;

Структура урока:

0. 1. Организационный момент; 2. Повторение ранее изученного материала; 3. Изучение новой темы; 4. Домашнее задание; 5. Подведение итогов;

1. Фрагмент урока:Приветствие учащихся.

Повторение ранее изученного материала: (учащиеся сами определили круг вопросов, задавали друг другу)

1. Что называется уравнением? (Уравнение – это равенство, содержащее одну или несколько переменных) - линейное уравнение с 1 переменной.

2. Что называется линейным уравнением с 2 переменными? ()

3. Приведите примеры линейных уравнений с 2 переменными.

4. Что является решение линейного уравнения с 2 переменными?

Задача 1: Разность двух чисел равна 6. Найдите эти числа. ()

5. Какие свойства уравнений вы знаете?

Свойства уравнений:- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

• если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Задания на усвоение материала:

1.Решите систему уравнений:

2. Построить график линейного уравнения 3x – 2y = 6

3. Известно, что график функции 2x + 3y = 2 проходит через точку А, ордината которой равна 4. Найдите абсциссу этой точки.

Билет № 15. Билет №15. Многочлены от одной переменной. Делимость многочлена на двучлен Кольцо f[X] многочленов над полем

Определение 5.1.Пусть дано произвольное полеF,x – переменная. Многочленом n - й степени от одной переменнойназывают выражение вида:a_n  xⁿ + …+ a₁ x + a₀, гдеa_i F(i= 0, 1, 2, …,n),a_n0 ,n  N {0}.

Замечание.a_i хⁱназывают членом многочлена;i– степенью этого члена (еслиa_i 0);a_i– коэффициент соответствующего члена. Еслиa_i= 0, то членуa_i  xⁱне приписывается никакой степени,a₀  x⁰ – член нулевой степени, еслиa_i0 – элемент поляF.

Многочлены от одной переменной обозначают так: f(x),g(x),h(x) и т.п.

Определение 5.2. Степенью многочленаf(x) называют наивысшую из степеней его членов (и обозначаютdegf(x)).

Многочлен f(x) = 0 ·хⁿ+ 0 ·x^n-1+ … + 0 называютнуль-многочленом. Его степень не определяется.

Множество многочленов F[x] = {f(x)|f(x) =a_n  xⁿ + …+ a₁ x + a₀} можно разбить на три класса:

1) нуль-многочлен f(x) = 0 ·хⁿ+ 0 ·x^n-1+ … + 0;

2) многочлены нулевой степени (a_i F);

3) многочлены степени выше нулевой f(x) иg(x), …

Если даны два многочлена f(x) иg(x), то всегда можно считать, что они содержат одинаковое число членов, т.к. недостающие члены всегда можно приписать с нулевыми коэффициентами.

Определение 5.3. f(x),g(x)F [x], если

f(x) = a_n xⁿ + a_n-1 x^n-1 + … + a₁ x + a₀ и

g(x) = b_n xⁿ + b_n-1 x^n-1 + …+ b₁ x+ b₀, то

f(x) = g(x)(a_n = b_n ) (a_n-1 = b_n-1) … (a₀=b₀).

Определим на множестве F[x] три операции:

1. f(x),g(x)F [x],f(x) +g(x) = (a_n +b_n) xⁿ +( a_n-1 +b_n-1 )x^n-1 + …+ (a₁ +b₁) x+ +(a₀ + b₀);

2. f(x) F [x], F , f(x) = a_n xⁿ +a_n-1 x^n-1 + … + a₁ x +a₀;

3. f(x), g(x) F [x], f(x) · g(x) = a₀ b₀ + (a₀ b₁ + a₁ b₀) х + …+ (a₀ b_i +…+a₁ b_i-1 + + … + a_i b₀ ) xⁱ + … + a_n b_m )x^n+m;

Теорема 5.1 (о кольце многочленов от одного переменного).

Алгебра (F[x], + , ) является коммутативным кольцом с единицей без делителей нуля, содержащим в качестве подкольца, поле F.