Приклади для самостійного розв’язку
Приклад 13. Знайти матрицю обернену до матриці
а)
б)
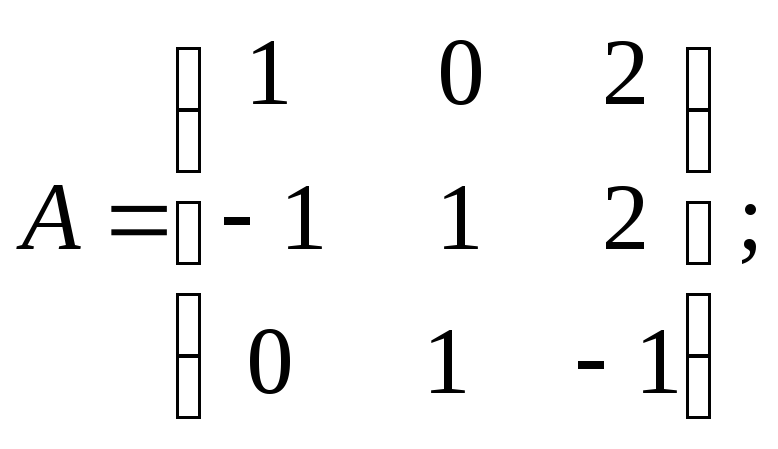в)
Відповідь:
а)
б)
в)
Приклад 14. Розв’язати матричне рівняння
а)
б)
в)
г)
Відповідь:
а)
б)
в)
г)
Розв’язання прикладів
Приклад 15. Розв’язати систему лінійних рівнянь за правилом Крамера, за допомогою матричного методу та методом Гаусса.
Розв’язання. I. Метод Крамера. Задана неоднорідна система 3-х лінійних алгебраїчних рівнянь з трьома невідомими. Основний визначник цієї системи
Тому, згідно з правилом Крамера, задана система має єдиний розв’язок, який знайдемо за формулами Крамера.
Спочатку знайдемо допоміжні визначники:
Тепер за формулами Крамера знаходимо:
Отже, розв’язком цієї системи буде (1;-1;1).
II. Матричний метод. Шукаємо розв’язок системи у вигляді X=A-1B, де
Визначник
цієї матриці
Для запису оберненої матриці A-1 знайдемо алгебраїчні доповнення елементів матриці А:
Отже,
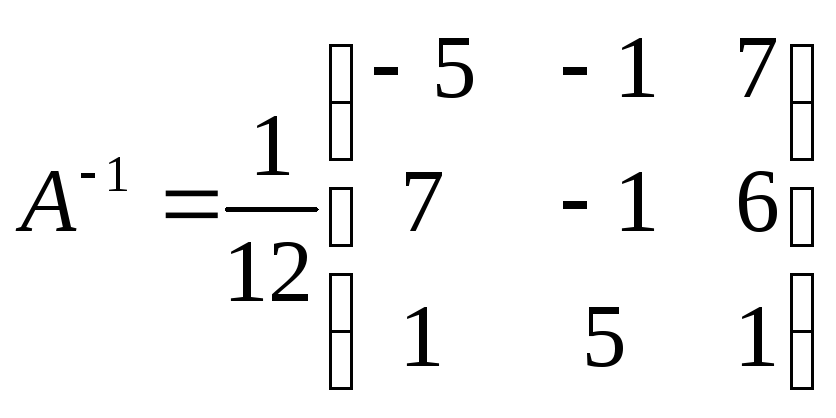
Тепер за формулою X=A-1B знаходимо розв’язок системи:
Отже, розв’язком цієї системи буде (1;-1;1).
III. Метод Гаусса. Виконаємо елементарні перетворення з розширеною матрицею.
Звідси
випливає
Отже, розв’язком цієї системи буде (1;-1;1).
Приклади для самостійного розв’язку
Приклад 16. Розв’язати систему лінійних рівнянь за правилом Крамера, за допомогою матричного методу та методом Гаусса.
а)
б)
в)
г)
Відповідь: а) (1;1;1), б) (-1;0;1), в) (0;1;1), г) (1;2;0).
Розв’язання прикладів
Метод Жордана – Ґаусса з використанням розрахункових таблиць
Алгоритм кроку перетворення Жордана – Ґаусса:
1.
обираємо розв'язувальний елемент 
;
2.
елементи i-го
рядка (його називають розв'язувальним)
ділимо на
і
запишемо в
і
рядок розрахункової таблиці;
3.
в розв'язувальному
j
стовпці замість
пишуть одиницю, а замість інших
елементів цього стовпця пишуть нулі;
4. усі інші елементи розрахункової таблиці, в тому числі і контрольного стовпця, знаходять за формулою
(1)
Обчислення
елементів
за
формулою
(1) доцільно
виконувати
з використанням схеми прямокутника
(-)
(+)
5. роблять перевірку правильності розрахунків шляхом порівняння суми елементів рядка з відповідним елементом контрольного стовпця.
Рекомендації для скорочення розрахунків
Розв'язувальним елементом доцільно обирати одиницю, тоді формули (1) спрощуються.
Якщо у розв'язувальному стовпці розрахункової таблиці є нулі, тоді відповідний рядок з цієї таблиці переписують без змін.
Якщо в розв'язувальному рядку розрахункової таблиці є нулі, тоді відповідний стовпець переписуємо без змін.
Наприклад, в і-му розв'язувальному рядку аіl = 0, тоді l-й стовпець таблиці переписуємо без змін.
Якщо в таблиці є два пропорційних рядки, тоді один з них можна закреслити.
Наступні кроки перетворень Жордана – Ґаусса виконуються таким же чином, при цьому кожного разу розв'язувальний елемент треба обирати з інших рядків та стовпців.
Приклад 17. Розв’язати методом Жордана – Ґаусса систему
Розв'язування будемо проводити з використанням розрахункової таблиці за допомогою формул (1).
|
x1 |
x2 |
x3 |
х4 |
х5 |
bi |
k |
|
|
1 |
1 |
1 |
1 |
1 |
7 |
12 | |
|
3 |
2 |
1 |
1 |
-3 |
-2 |
2 | |
|
0 |
1 |
2 |
2 |
6 |
23 |
34 | |
|
5 |
4 |
3 |
3 |
-1 |
12 |
26 | |
|
1 |
1 |
1 |
1 |
1 |
7 |
12 | |
|
0 |
-1 |
-2 |
-2 |
-6 |
-23 |
-34 | |
|
0 |
1 |
2 |
2 |
6 |
23 |
34 | |
|
0 |
-1 |
-2 |
-2 |
-6 |
-23 |
-34 | |
|
1 |
0 |
-1 |
-1 |
-5 |
-16 |
-22 | |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 | |
|
0 |
1 |
2 |
2 |
6 |
23 |
34 | |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблиця
Отже, задана система сумісна і має множину розв’язків. Базисні невідомі х1 та х2, вільні невідомі х3, х4 та х5.
Загальним розв’язком заданої системи буде
