28. Аподизація

Під аподизацією, як правило, розуміють покра- щення апаратної функції.

Апаратна функція (АФ) – це реакція приладу на си- гнал у вигляді -функції, є важливою характеристикою будь-якого спектрометра, у т. ч. і фур’є- спектрометра. Для визначення АФ фур’є-спектрометра подаємо на його вхід монохроматичний сигнал виду . Спектр цього сигналу:

. (4.43)

З іншого боку, за теоремою Вінера-Хінчина квад- рат модуля спектра визначається як

(4.44)

де

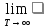(4.45)

Проте у реальному приладі неможливо забезпечити нескінченні межі затримки при застосуванні рівняння (4.44), можливо забезпечити у межах віддо- максимальне переміщення дзеркала (рис. 4.11). Тоді:

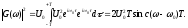(4.46)

Вираз (4.46) є імпульсним відгуком або АФ фур’є-спектрометра. Ширина цієї функції визначена з умови (див. рис. 4.11)

(4.47)

тобто,

(рад), (4.48)

Якщо виразити ширину АФ у см–1, то маємо

(см) (4.48)

Навіть при = 1 см маємо= 1 см, що у види- мій області (500 нм) складає 0,025 нм, а у області 5 мкм відповідно 2,5 нм, що цілком пристойно для багатьох практичних потреб. Аподизація. Квадратичний детектор реагує на наявність енергії, тому результуюча зареєстрована функція є квадрат модуля спектраУ ряді випадків це незручно: відгук на малий сигнал у околі потужного може сприйматися як пелюсток АФ цього потужного сигналу, інакше кажучи, загубитися у схожих зовні вторинних сплесках відгуку на потуж- ний сигнал. Аналіз показує, що пелюстковість результату ПФ з’являється тоді, коли під інтегралом (4.46) знаходиться функція, яка різко змінюється. У оптиці саме такі задачі є типовими, оскільки світлові потоки обмежуються екранами, діафрагмами, зреш- тою, оправами, які автоматично вмонтовують функцію Хевісайда (функцію включення) у будь-який

Рис. 4.13. Вигляд аподизуючих функцій:

(Крива 1); (2)(3).

сигнал. Навіть саме увімкнення-вимкнення реєстрації означає наявність двох функцій Хевісайда!

Вихід було знайдено у тому, щоб ПФ виконувати не у межах «прямокутного вікна» а з поступовим затуханням на границях діапазону, штучно ввівши під інтеграл відповідну вагову функцію. Приклади таких функцій наведено на рис. 4.13. Для абсолютно моно- хроматичного сигналу з функцією включення типу 1 отримаємо розподіл енергії у спектрі

(4.50)

Де

(4.51)

(4.52)

(4.52)

Тут використано табличне значення інтегралу Таким чином,

(4.53)

Порівняємо розподіл енергії у спектрі (4.53), отри- маний з використанням аподизації із неаподизованим випадком (4.51): енергія зменшилась вдвічі, хід функ- ції більш плавний, хоча вона формально вдвічі ширша. У цьому випадку говорять про напівширину АФ, ма- ється на увазі ширина функції на половині її максимального значення, тому теоретично вона зрос- тає лише на 48 %. При використанні більш «лагідної» аподизуючої функції виду напівширина зростає на 58 %, а із функцією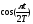лише на 31 % (проявляється, все ж таки, незначна різкість включення). Крім того, значно зменшуються вторинні пелюстки АФ, у наведеному випадку перший з них майже у 5 разів, другий – майже у 8 (рис. 4.14).

29. Граничні можливості фур’є-спектроскопії

Фур’є-спектроскопія – розділ спектроскопії, але, разом з тим, самостійна оригінальна відносно молода перспективна наука зі своїми теоретичними, інструментальними і практичними засадами, проте також і з традиціями. Є ряд особливостей, на яких варто зупинитися. Для будь-якого спектрометра ключовими є питання про світлосилу та роздільну здатність.

Виграш Жакіно полягає у тому, що інтенсивність світла реєструється у області максимуму центральної плями ІК (на противагу спектрометрам з призмою, де реєструється світло, що пройшло крізь дві вузькі щілини). Скористаємось моделлю інтерферометра, у якому уявні джерела знаходяться на нескінчен-

Рис. 4.14. Спектр функції G() (1) та спектральна залежність реакції детектора на монохроматичну лінію частоти 0 :

2 - без аподизації; 3 - з аподизацією типу (1– ||/T).

ності і на відстані одне від одного (рис. 4.15). У площині реєстрації хвилі майже плоскі, тому ІК спо- стерігається у фокальній площині об’єктива Об. Як видно із рис. 4.15

(4.54)

де порядок інтерференційного максимуму відповідає центру ІК, а– деякій ближній периферії ІК. Фотодетектор Ф використовуємо з такою площадкою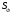яка точно дорівнює розміру центрального світло-

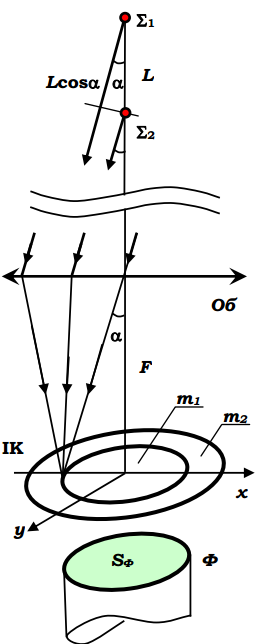
Рис. 4.15. Реєстрація світлового потоку у фур’є- спектрометрі у межах центральної світлової плями.

го кільця , тобто, діаметрвідповідає діаметру першого темного кільця). Тоді з (4.54) маємоабо

, (4.55)

де саме відповідає випадку. З іншого бо ку, якщо ІК сформована об’єктивом з фокальною відстанню, то з центра об’єктива площадкуно під тілесним кутом ви

(4.56)

Роздільна здатність будь-якого інтерферометра R залежить від числа променів N та максимального порядкуі представляється із врахуванням (4.55), (4.56) формулою, тобто

. (4.57)

Звичайно, формула (4.57) вказує на теоретичну те- нденцію, на практиці слід враховувати розмір джерела, залежність геометрії ІК від перебігу поряд- ків, проте реальний виграш, у порівнянні з призмовим приладом складає кілька десятків разів. Виграш Фелжета. Послідовний запис спектру традиційною апаратурою відбувається наступним чином. Якщо роздільну здатність приладу позначити , то увесь цікавий нам діапазон спектрурозпадається наканалів, причому. Використовувати більш, ніжканалів немає сенсу, – роздільна здатність при цьому не покращується. Якщо ж кіль- кість каналів менше, то роздільна здатність буде гіршою, а це означає погіршення інформативності запису. Повна інтенсивність джерела у діапазоніє

де – інтенсивність у межах одного каналу, заради простоти вважаємо, що скрізь однакова. Якщо рівень шуміву системі реєстрації носить нормальний ха-

рактер, тобто, то то при такій послідовній реєстрації кінцеве значення дуже важливого параметра сигнал/шум має вигляд

(4.58)

При реєстрації того ж діапазону 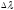за допомогою фур’є-спектрометра всікомпонентівреєструються одночасно у межах центрального інтерференційного максимуму:

(4.59)

рівень шуму дорівнює відповідно

(4.60)

а відношення типу (4.58)

(4.61)

Із порівняння формул (4.58) та (4.61) видно, що фур’є-спектрометр має переваги перед традиційними щілинними спектральними приладами у характерис- тиці сигнал/шум у сотні-тисячі разів, оскільки реально. Ця перевага носить назву ви- граш Фелжета і особливо важлива при реєстрації світла слабких джерел, наприклад, у астрономії.