Paly_I_A__Prikladnaya_statistika_Uchebnoe_po

лежат на горизонтальной прямой, то все частные средние y i равны y .

y i = y , i = 1,2, … , k ηyx = 0.

Тогда говорят об отсутствии связи между значениями x и у. Если все точки на диаграмме рассеяния сгруппированной выборки лежат на некоторой прямой (кроме горизонтальной), то ηyx = 1. В остальных случаях

0 < ηyx < 1.

Величина ηyx зависит от группировки. Как правило, с ростом числа интервалов группировки по переменной x корреляционное отношение растет. По аналогии с числом ηyx можно рассчитать число ηxy ≠ ηyx, если считать x зависимой переменной, а у – независимой переменной.

Пример. На металлообрабатывающем заводе у 60 марок стали провели замеры предела текучести F(x, кг/мм2) и предела прочности σв (y, кг/мм2). В итоге получили 60 пар значений, представленных в табл. 3.6. Предполагается, что большие значения F обуславливают большие значения σв; марки стали с низким пределом текучести имеют и низкий предел прочности. Для обоснования гипотезы о высокой положительной корреляции между пределом прочности и пределом текучести сгруппируем выборку (табл. 3.7) и рассчитаем числовые характеристики.

Внешний вид табл. 3.7 несколько отличается от вида табл. 3.5, иллюстрирующей двумерную группировку. Табл. 3.7 построена так, чтобы можно было легко вообразить диаграмму рассеяния, не строя ее саму.

Имеем:

n = 60; k = 7; m = 8; hx = hy = 20 (длины интервалов группировки).

y= 601 (200*2 + 180*2 + 160*5 + 140*9 + 120*13 + 100*14 + 80*10

+60*5) = 114,7;

∑7 (y i − y )2 n i = 8*(67,5 – 114,7)2 + 4*(105 – 114,7)2 + 13*(100 – 114,7)2 +

i =1

+15*(113,3–114,7)2 + 9*(131,1–114,7)2 +7*(154,3–114,7)2 +4*(190 – 114,7)2 = = 57115,8;

∑8 (y j − y )2 l j = 2*(200 – 114,7)2 + 2*(180 – 114,7)2 + 5*(160 – 114,7)2 +

i =1

+9*(140 – 114,7)2 + 13*(120 – 114,7)2 + 14*(100 – 114,7)2 +10*(80 – 114,7)2 + +5*(60 – 114,7)2 = 69493,4;

ηyx = 0,82.

Для справки: коэффициент корреляции r = 0,92, предел прочности и предел текучести связаны сильной линейной зависимостью.

3.9.ЗАДАЧИ

1. Как выражаются коэффициенты линейного уравнения регрессии через выборочный коэффициент корреляции r ?

2. Показать, что выборочный коэффициент корреляции r не изменится, если значения хi, уi подвергнуть преобразованию: хi = хi + a; уi = уi + b;

i = 1,2, ... , n. Как изменится выборочный коэффициент корреляции r, если все числа хi умножить на одно и то же число d, все числа y умножить на одно и то же число b, i = 1,2, ..., n?

3. В соответствии с методом наименьших квадратов составить систему уравнений для определения коэффициентов следующих уравнений

регрессии:

у = a + bex, y = a + b·sinωx + с·cosωx

(ω – заданное число), y = a + xb .

В задачах 4 - 19 нужно найти числовые характеристики выборки и определить (если r ≥ 0,7) коэффициенты линейного уравнения регрессии х на у, если у можно принять за независимую переменную.

4. Результаты тестирования (баллы) 10 студентов. Первый тест проверяет память (x), второй - способность к логическому мышлению (у):

5. Оценка за тест по способностям (х) шести продавцов–практикантов и результаты их работы за первый год (у) в сотнях фунтов проданного товара:

6. Снашивание (х) и твердость (у) резины в условных единицах:

7. Масса поросят (у) в килограммах в зависимости от возраста (х) в неделях:

8. В книге «Основы химии» Д.И.Менделеева приводятся данные о растворимости азотнокислого натрия NaNO3 в зависимости от температуры воды. Указывается, сколько условных частей NaNO3 (у) растворяется в 100 частях воды при соответствующих температурах в oС

(х):

13. Число айсбергов, наблюдавшихся помесячно к югу от Ньюфаундленда (х) и к югу от Большой отмели (у) за 1920 г.:

14. Число разводов на 1000 жителей в 20 штатах США (у), средний доход на семью (x1) в тыс. долл.; процент городского населения (х2):

15. На сталелитейном заводе обследовали 15 плавок определенного сорта стали. Учитывался угар кремния (х), измеряемый в процентах, и выход стали (у), также измеряемый в процентах.

16. Продолжительность послеоперационного лечения в клинике (у) в днях и возраст больных (х) в годах, оперировавшихся по поводу грыжи:

17. При исследовании некоторой химической реакции через каждые 5 минут определялось количество вещества (у) в %, оставшееся в системе. Подобрать коэффициенты уравнения у = а + bх + сх2, где х – время после начала реакции в минутах.

18. Барометрическое давление связано с высотой следующим

p0 и k - параметры.

По методу наименьших квадратов оценить значения параметров k/T и р0 по результатам наблюдений, проведенных при постоянной температуре:

Подобрать коэффициенты функциональной зависимости p = aVb. 20. Функциональная зависимость удельного сопротивления

кристаллического кварца ρ (Ом·см) от абсолютной температуры Т (K)

a1+b

имеет вид ρ=10T .

Используя опытные данные, оценить значения параметров а и b.

21. Получена выборка наблюдений переменных х и у:

Для представления этих данных предлагается выбрать лучшую из предложенных моделей:

1) y = a +xbx . 2) y = ba x . 3) y = bxa . 4) y = a ln(x) + b .

Оценить значения параметров а и b.

22. На заводе производят некоторый материал, твердость которого хотят повысить. Для этого увеличивают содержание некоторого химического вещества. Ниже приведены данные для 20 случайно отобранных образцов. Значения у – твердость образца (условные единицы), значения х – процентное содержание химического вещества относительно некоторого уровня.

Подобать коэффициенты линейного и параболического уравнений регрессии. Какое из уравнений больше соответствует экспериментальным данным?

6. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПО КРИТЕРИЮ ПИРСОНА (КРИТЕРИЮ χ2)

Те, что веруют слепо, - пути не найдут. Тех, кто мыслит, - сомнения вечно гнетут. Опасаюсь, что голос раздастся однажды: «О, невежды! Дорога не там и не тут?»

О. Хайям (перевод Г. Плисецкого)

6.1. ПРИМЕР

Рассмотрим такую ситуацию. 200 электронных ламп, выбранных наудачу из большой партии, испытывались на продолжительность работы. Результаты (в часах) таковы (табл. 6.1):

Хотелось бы дать разумный ответ на такие вопросы: какую продолжительность работы следует ожидать, если взять наудачу лампу из этой же партии? Какова вероятность, что лампа проработает не менее 1000 часов? Какова вероятность того, что лампа проработает менее 200 часов?

Ответить на эти вопросы легко, если известен закон распределения случайной величины Х – времени работы лампы. Но его-то мы не знаем. Мы располагаем только выборкой (правда, достаточно большой, n = 200) из генеральной совокупности X. Попробуем, пользуясь этой выборкой, подобрать подходящий закон распределения.

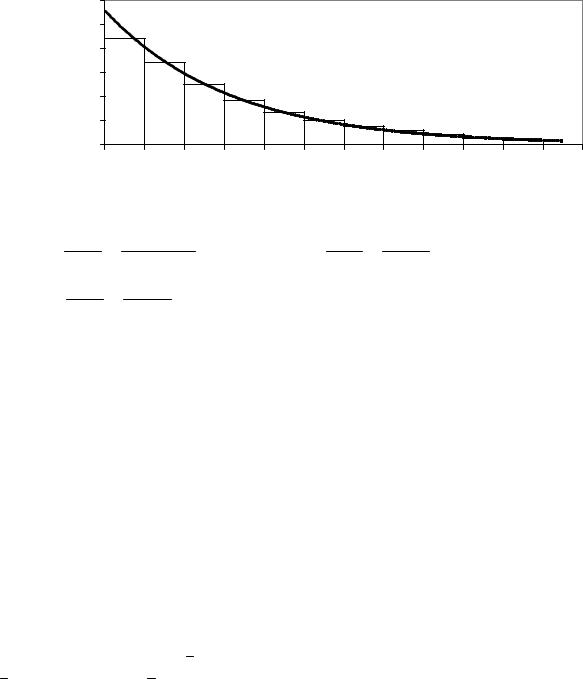
Построим прежде всего гистограмму (рис. 6.1).

h i , f(x)

h7 = 0,00015; h8 = 0,00012; h9 = 0,00008; h10 = 0,00005; h11 = 0,00003.

Гистограмма – аналог графика функции плотности вероятности. В нашем случае гистограмма очень похожа на график функции плотности показательного закона. Мы вправе предположить, что большая выборка хорошо представляет генеральную совокупность и что если гистограмма похожа на график экспоненты, то это означает, что выборка извлечена из генеральной совокупности, распределенной по показательному закону с функцией плотности вероятности

f(x) = λe-λx.

Однако показательный закон зависит от одного параметра – числа λ. Чтобы полностью описать закон, нужно знать, чему равно λ. Подберем значение λ по выборке, причем поступим самым бесхитростным способом. Как известно, математическое ожидание случайной величины, имеющей показательное распределение, М(Х) = 1/λ. Если наша выборка хорошо представляет генеральную совокупность, мы вправе полагать, что значение выборочного среднего x не слишком отличается от М(Х). Поэтому найдем x и положим λ=1/ x .

x = 2001 (150 53 + 450 41 + 750 30 +1050 22 +1350 16 +1650 12 + +1950 9 +2250 7 + 2550 5 + 2850 3 + 3150 2) =871,5(ч) .

Тогда λ = 1/ x ≈ 0,00115, f(x) = 0,00115e -0,00115x ,x ≥ 0.

Вычислим значения f(х) на границах интервалов (табл. 1.2) и построим график функции плотности вероятности прямо на гистограмме

(см. рис. 6.1).

Не следует увлекаться слишком большим количеством значащих цифр, ведь все наши данные достаточно приближенные.

Кривая функции плотности вероятности f(х) очень «ладно» легла на гистограмму. Такое хорошее совпадение гистограммы и графика f(х) прибавляет уверенности в том, что закон распределения генеральной совокупности Х выбран достаточно точно.

Попробуем теперь оценить числом расхождение между экспериментальными данными и тем, что должно быть «по теории».

Мы можем вычислить теоретическую вероятность рi попадания случайной величины X, распределенной по показательному закону с функцией плотности f(x) = 0,00115е-0,00115x, x ≥ 0 в интервал [xi-1, xi).

р(хi-1 < X < xi) = e−λxi−1 − e−λxi = e−0,00115xi−1 − e−0,00115xi .

Зная вероятность pi, можно вычислить математическое ожидание числа попаданий случайной величины Х в интервал [xi-1, xi) в результате n независимых испытаний, оно равно nрi. Теперь можно найти разность

ni - nрi между числом вариант выборки, попавших в интервал [хi-1, хi), и ожидаемым числом попаданий. Чтобы оценить суммарное расхождение между теоретическими и опытными данными, нужно сложить все полученные разности. Чтобы положительные и отрицательные разности не уничтожили друг друга, возведем их в квадрат. Кроме того, важно не абсолютное значение ni - nрi, а относительное (ni,- npi)/npi. Действительно, если ni = 0, nрi = 1, это совсем не одно и то же, что в случае, когда ni = 10, nрi = 11. Относительное отклонение в первом случае равно 1, а во втором − только 1/11.

Итак, вычислим прежде всего вероятности рi.

р1 = P(0 < X < 300) = e-λ*0 - e-λ*300 = e 0 - e –0,345 = 1- 0,708 = 0,2918; p2 = P(300 < X < 600) = e-λ*300 - e-λ*600 = 0,7082 – 0,5016 = 0,2066; р3 = P(600 < X < 900) = e-λ*600 - e -λ*900 = 0,1464;

р4 = 0,1036; р5 = 0,0734; р6 = 0,052; р7 = 0,0368; р8 = 0,0261;

р9 = 0,0185; р10 = 0,0131; р11 = 0,0092.

Дальнейшие вычисления приведены в табл. 6.3.

Таблица 6.3

Сумма вероятностей pi равна 0,9775. Это значит, что интервал [0; 3300) охватывает практически все возможные значения выбранного нами теоретического закона. Сумма чисел последнего столбца традиционно обозначается буквой χ2 (читается «хи - квадрат»). В нашем случае

Много это или мало?

6.2. НЕМНОГО ТЕОРИИ

Только что мы находили число χ2.

(генеральной совокупности) в i-й интервал;

n – число независимых испытаний (объем выборки);

nрi – математическое ожидание числа попаданий случайной величины Х в i-й интервал

Но на приведенную формулу можно посмотреть и по-другому. Вместо числа ni рассмотрим случайную величину ni (в математической статистике случайные величины и их значения часто обозначаются одними и теми же маленькими буквами). Случайная величина ni - это число появлений