3.2. Построение диаграмм кинетической энергии, приведенного момента инерции звеньев механизма и энергомасс. Определение момента инерции маховика.

Кинетическая энергия механизма равна сумме кинетических энергий его звеньев:

где во всех положениях механизма.

- момент инерции кривошипа ОА (в таблице)

=– кинетическая энергия шатуна АВ

где - момент инерции шатуна АВ, относительно оси, проходящей через центр масс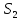(таблица)

=- кинетическая энергия поршня 3

=- кинетическая энергия шатуна АС

=- кинетическая энергия поршня 5

Приведенный момент инерции I_n звеньев механизма вычисляем по формуле

и сводим результаты в таблицу.

Таблица №6. Значения кинетической энергии и приведенного момента инерции звеньев механизма

Положения	Т2, Дж	Т3, Дж	Т2+ Т3 Дж	Т4, Дж	Т5, Дж	Т4+ Т5 Дж	Т Дж	In, кг м2
0	295,9	0	295,9	551,1	459,3	1010,4	1488,3	0,09405
1	344,2	73,9	418,1	458,7	269,1	727,8	1327,9	0,08392
2	458,7	269,1	727,8	344,2	73,9	418,1	1327,9	0,08392
3	551,1	459,3	1010,4	295,9	0	295,9	1488,3	0,09405
4	522,1	431,4	953,5	359,8	73,9	433,7	1569,2	0,09916
5	381,1	164,7	545,8	458,7	269,1	727,8	1455,6	0,09199
6	295,9	0	295,9	551,1	459,3	1010,4	1488,3	0,09405
7	381,1	164,7	545,8	522,1	431,4	953,5	1681,3	0,10625
8	522,1	431,4	953,5	381,1	164,7	545,8	1681,3	0,10625
9	551,1	459,3	1010,4	295,9	0	295,9	1488,3	0,09405
10	458,7	269,1	727,8	381,1	164,7	545,8	1455,6	0,09199
11	344,2	73,9	418,1	522,1	431,4	953,5	1553,6	0,09818

Строим диаграмму кинетической энергии механизма в масштабе 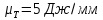, которая одновременно является и диаграммой приведенного момента инерции, построенной в масштабе

Строим диаграмму энергомасс, исключая параметр 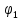из диаграмми.

Для этого строим прямоугольную систему координат .

Из начала координат проводим прямую под углом 45º к оси

По заданному коэффициенту неравномерности движения 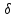и средней угловой скоростиопределяем углыпо формулам

где

К диаграмме энергомасс . проводим 2 касательные под угламиЭти касательные отсекут на оси ординат отрезокKL, который определяет кинетическую энергию маховика в масштабе

По формуле вычисляем момент инерции маховика

Определяем диаметр маховика

Определяем массу маховика

Ширина маховика

b=q

где q- относительная ширина маховика q=(0,15…0,2)