Дисперсия

Дисперсия света (от лат. Dispersio - рассеяние). Для прозрачных бесцветных веществ график зависимости n(λ) в видимой части спектра имеет вид, показанный на рис. 26. Интервал длин волн, в котором dn/dλ< 0 (как на ри­сунке 1), соответствует нормальной дисперсии. Те же интервалы длин волн, где дисперсия вещества dn/dλ > 0 соответствуют аномальной дисперсии. На рис. 27 показан график зависимо­сти n(λ) с участками нормальной и аномальной дисперсии. За­метим, что область аномальной дисперсии совпадает с полосой поглощения .

Все вещества в той или иной степени являются диспергиру­ющими. Как показали тщательные исследования, не обладает дис­персией только вакуум .

Рисунок 26	Рисунок 27

Элементарная теория дисперсии

Пусть электрон перемещается вдоль . Когда электрон движется с ускорением, на него действует сила Лоренца, пропорциональная скорости и обратная ей по направлению. Тогда поII-му закону Ньютона:

.

Обозначим и перепишем это .уравнение в виде:

.

Это линейное дифференциальное уравнение затухающих колебаний под действием вынуждающей силы второго порядка. Решим сначала соответствующее однородное уравнение: . Для этого сделаем подстановку Эйлера:. Тогда. Тогда общее решение этого уравнения:

.

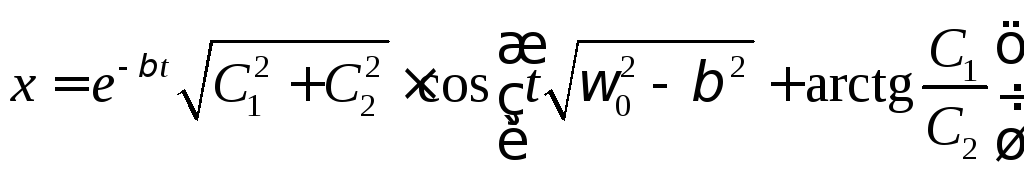Найдём частное решение в виде

.

Подставим частное решение в диф. уравнение: ,

т.е.

,

следовательно,

.

Решением уравнения будет сумма общего и частного решений, но из-за общее решение стремиться к 0 прии через какое-то время общее решение будет оказывать пренебрежимо малое воздействие на установившийся режим. Таким образом,.

Показатель преломления , где – диэлектрическая проницаемость среды. , где. Здесь– напряжённость электрического поля в веществе, – поляризованность диэлектрика. Сделаем мультидипольное разложение: , где– концентрация ядер,– концентрация электронов (т.к. у электронов собственная частота может быть разная, например – у электронов, находящихся на разных электронных оболочках). Сумма первых двух слагаемых в случае неполярных молекул равна 0, и, таким образом,. Тогда

.

Величина обычно очень маленькая, следовательно,

.

Причиной дисперсии является то, что при прохождении света через вещество в коллективе электронов возбуждаются колебания, которые находятся в квазиупругом состояния и имеют собственные частоты колебаний. Скорость распространения волны в веществе обратно пропорциональна , а пропорционален амплитуде колебаний электронов, которая, в свою очередь, зависит от того, насколько частота возбуждающей электромагнитной волны отличается от колебаний электрона.

Разрыв функции ε (ω) при ω = ω0 и обращение ее в не имеют физиче­ского смысла, это получилось вследст­вие пренебрежения затуханием (β - 0). Если же его учесть, то ход кривой будет иным (рис. 28) и достаточно хоро­шо подтвер­ждается эксперимен­тально (сравните с рис. 27). Зависимость κ(ω) характеризует полосу поглощения. Как раз с ней совпадает об­ласть аномальной дисперсии (dn/dω < 0).
	Рисунок 28

Волновой пакет. Строго монохроматическая волна — это идеализация. Таких волн в природе нет. Любая реальная вол­на, согласно теореме Фурье, может быть представлена как су­перпозиция монохроматических волн с различными амплиту­дами и частотами ω в некотором интервале Δω. Суперпозицию волн, мало отличающихся друг от друга по частотам (Δω«ω), называют волновым пакетом или группой волн. Вид волнового пакета в некоторый момент времени показан на рис. 29. В его пределах монохроматические составляющие усиливают друг друга, вне пакета практически гасят друг друга.

	В вакууме все монохроматические волны, образующие па­кет, распространяются, как уже было сказано выше, с одинако­вой фазовой скоростью ,где k — волновое число (2π/λ). С такой же скоростью распро­страняется в вакууме и сам волновой пакет, не изменяя своей формы.
Рисунок 29

Групповая скорость. В диспергирующей же среде волновой пакет расплывается, поскольку скорости его монохроматиче­ских составляющих отличаются друг от друга, и понятие ско­рости такой волны требует уточнения.

Пусть складываются две волны: . Разность фаз. Приращение разности фаз. Перейдём в такую систему отсчёта, что, т.е. в систему отсчёта, связанную с движением «горба» биения. Тогда.

Групповая скорость

.

Т.к. , то

.

Явления, связанные с зависимостью , называются дисперсионными, а величина– дисперсией вещества.

Если , то дисперсия называется нормальной, если– аномальной.