1. 1. 4. Ускорение. Мгновенное и среднее ускорение. Нормальное и тангенциальное ускорения.

Скорость частицы () может изменяться со временем как по величине, так и по направлению.Быстрота изменения вектора называется ускорением . Как и быстрота изменения любой функции по времени, ускорение определяется производной векторапоt. Таким образом, по определению ускорения получаем:

(1.9)

Разложение вектора по базису прямоугольной декартовой системы координат: .

Проекции вектора ускорения на оси координат определяются выражениями:

(1.10)

Модуль вектора ускорения:

(1.11)

Единица измерения ускорения - 1 м/с^2.

Средним ускорением точки в интервале времени от t до t + ∆t называется вектор , равный отношению изменения вектора скорости точки за этот промежуток времени к его продолжительности:

.

(1.12)

Определим ускорение произвольно движущейся точки.

В общем случае траектория точки представляет из себя простран­ственную кривую. Введем следующие понятия:

Соприкасающейся плоскостью в точке М траектории называется предельное положение плоскости, проходящей через любые три точки траектории, когда эти точки неограниченно приближаются к точке М.

Соприкасающейся окружностью в точке M траектории называется предельная окружность, полученная из произвольной окружности проходящей через три точки траектории при их неограниченном приближении к точке М.

Соприкасающаяся окружность лежит в соприкасающейся плоскости.

Центр соприкасающейся окружность и ее радиус называются соответствен­но центром кривизны и радиусом кривизны рассматриваемой кривой в точке М.

Прямая, соединяющая точку М с центром кривизны называется главной нормалью к кривой в точке М.

Cначала найдем ускорение точки равномерно переме­щающейся по окружности радиуса (см. рис. 1.3). Скорость направлена по касательной к окружности. Для двух положений точки:M1 в момент времени t и M2 в момент времени t + ∆t имеем векторы скоростей исоответственно. Из рис. 1.3 видно, что треугольник, образо­ван­ный этими векторами и вектором изменения скорости, и равно­бедренный треугольник с боковыми сторонами, равными радиусу

Рисунок 1.3.

окруж­ности и перемещение точки подобны. Следовательно,

Ускорение может быть представлено в виде:

,

(1.13)

где - единичный вектор нормали к круговой траектории движения точки (направлен к центру кривизны траектории).

Представим вектор скорости в виде:

(1.14)

где - единичный вектор, направленный по касательной к окружности и указывающий направление скорости, – величина скорости, т.е. ее численное значение.

При равномерном движении модуль скорости равен константе ( = const), меняется только направление вектора касательной. Тогда для такого случая:

.

(1.15)

Сравниваем с формулой ускорения через (1), получим:

.		(1.16)
	При равномерном движении ускорение направлено к центру, т.е. перпендикуляр траектории, но не так будет обстоять дело, когда скорость   const. В общем случае произ­вольной гладкой кривой радиус кривизны меняется от точки к точке (см., например, рис. 1.4). Непрерывно меняется и направление единичного вектора главной нормали . Рассмотрим этот случай. Имеем тогда
Рисунок 1.4.

Применяем подстановку, исходя из формул (1.13) и (1.15) получаем:

(1.17)

Заменим на(тангенциальное ускорение), а на(нормальное ускорение), получим

.

(1.18)

Тангенциальное ускорение меняет скорость по величине, нормальное ускорениеменяет скорость по направлению.

Действительно, если дана некая траектория (см. рис. 1.5) есть скорость в начале и скорость во втором положении, перенесем параллельным переносом вектор в точку M₁, тогда мы видим, что вектор скорости получает приращение .

В результате, если уменьшать промежутки времени t к нулю, то оба соотношения (см. рис. 1.6) ибудут стремиться к пределам

Рисунок 1.5.		Рисунок 1.6.

и .

Пример .		Пример: Снаряд выпущен с начальной скоростью V = 200 м/с под углом  = 60 к горизонту. Определить кривизну траектории в точке наивысшего подъема снаряда (Рис.1.7). Силами аэродинамического соп­ротивления пренебречь.
	Рисунок 1.7.	Решение:
	В верхней точке
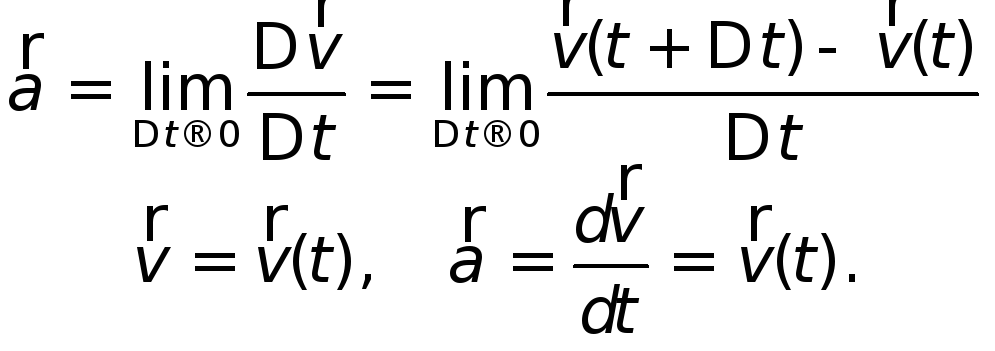
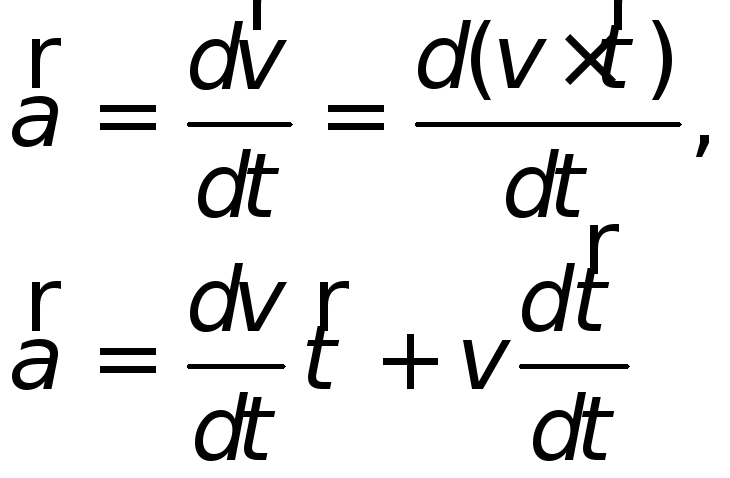
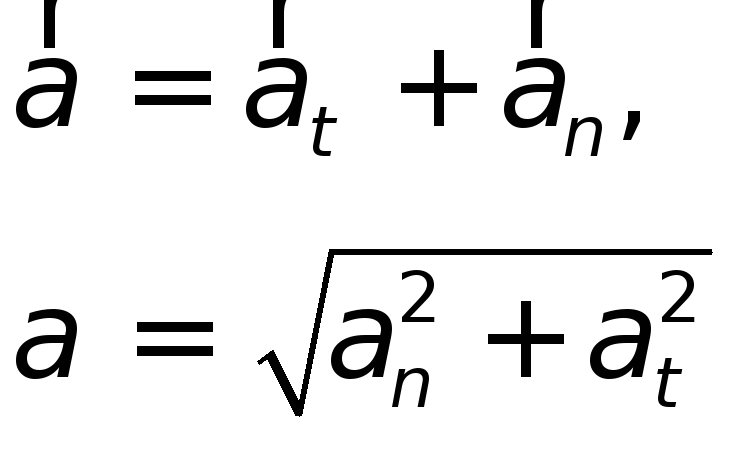