физика / formuly_2

Основные формулы

для решения задач

по общему курсу физики

(разрешается пользоваться при решении экзаменационных задач)

Составил:

Ст. преподватель кафедры физики ПГТУ

Федун В.И.

• Лоренцово сокращение длины и замедление хода движущихся часов:

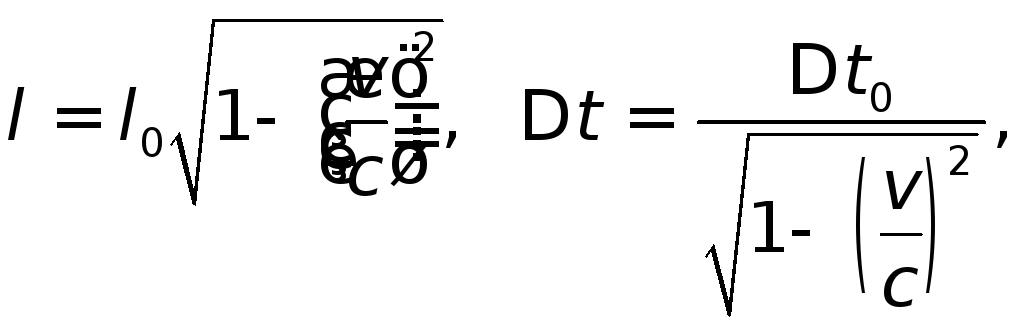
где – собственная длина, – собственное время движущихся часов.

• Преобразование Лоренца:

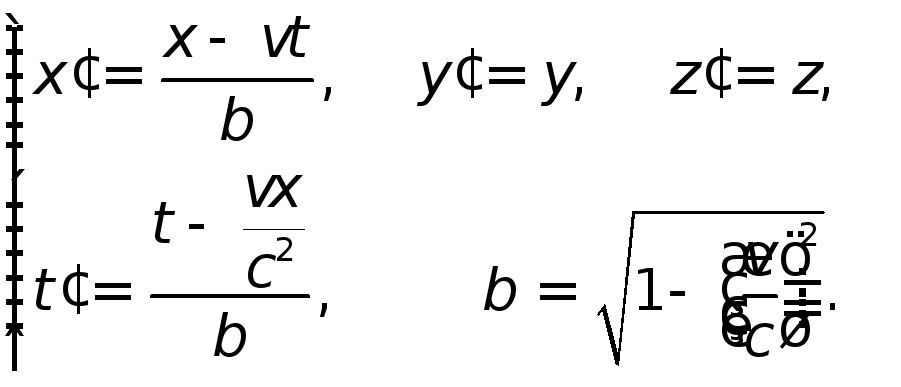
• Интервал – инвариантная величина:

где – промежуток времени между событиями 1 и 2, – расстояние между точками, где произошли эти события.

• Релятивистский импульс:

где 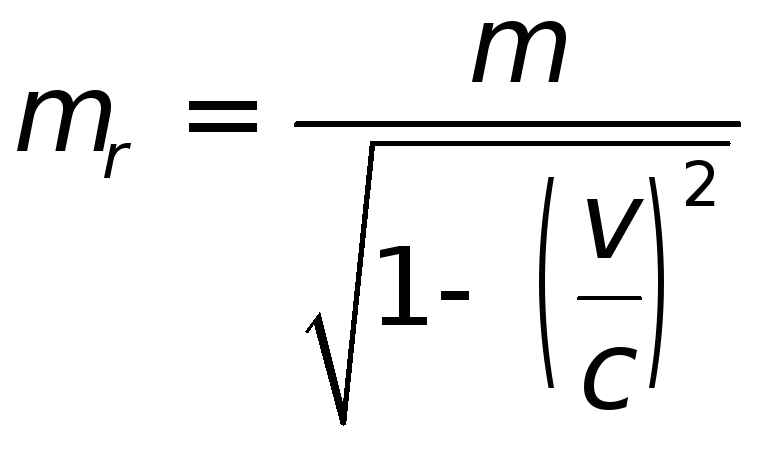– релятивистская масса, – масса (покоя).

• Релятивистское уравнение динамики частицы:

где – релятивистский импульс частицы.

• Полная и кинетическая энергии релятивистской частицы:

• Связь между энергией и импульсом релятивистской частицы:

• При рассмотрении столкновения частиц полезно использовать инвариантную величину:

где и – полная энергия и импульс системы до столкновения, – масса образовавшейся частицы (или системы).

Механические колебания и волны

• Уравнение гармонических колебаний

где – смещение колеблющейся точки от положения равновесия; – время; , , – соответствующая амплитуда, круговая (циклическая) частота, начальная фаза колебаний; – фаза колебаний в момент .

• Круговая частота колебаний

или

где и – частота и период колебаний.

• Амплитуда результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящими по одной прямой определяется по формуле

• Дифференциальное уравнение гармонических колебаний материальной точки

или

где – масса точки; – коэффициент квазиупргой силы ().

• Дифференциальное уравнение затухающих колебаний

или

где – коэффициент сопротивления; – коэффициент затухания (); – собственная круговая частота колебаний ().

• Уравнение затухающих колебаний (решение дифференциального уравнения затухающих колебаний)

где – амплитуда колебаний в момент ; – их круговая частота.

• Логарифмический декремент колебания

где и – амплитуды двух последовательных колебаний, отстаящих по времени друг от друга на период.

• Дифференциальное уравнение вынужденных колебаний

или

где – внешняя периодическая сила, лействующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; – ee амплитудное значение; .

• Амплитуда вынужденных колебаний

• Резонансная частота и резонансная амплитуда

и

• Уравнение плоской волны

или

где – смещение точек среды с координатой в момент ; – круговая частота; – скорость распространения колебаний в среде (фазовая скорость); – волновое число (, – длина волны).

• Длина волны связана с периодом колебаний и частотой соотношениями

и

• Разность фаз колебаний двух точек среды, расстояние между которыми (разность хода) равно

где – длина волны.

Магнитное поле постоянного тока

• Закон Био-Савара-Лапласа

где – магнитная индукция поля, создаваемого элементом проводника с током; – магнитная проницаемость; – магнитная постоянная ( Гн/м); – вектор, равный по модулю длине проводника и совпадающищий по направлению с током (элемент проводника); – сила тока; – радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора выражается формулой

где – угол между векторами и .

• Магнитная индукция в центре кругового проводника с током

где – радиус кривизны проводника.

• Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током

где – расстояние от оси проводника.

• Магнитная индукция поля, создаваемого отрезком проводника

• Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси)

где – число витков, приходящихся на единицу длины соленоида; – сила тока в одном витке.

• Закон Ампера. Сила, действующая на проводник с током в магнитном поле

где – сила тока; – вектор, равный по модулю длине проводника и совпадающий по направлению с током; – магнитная индукция поля.

Модуль вектора определяется выражением

где – угол между векторами и .

• Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами и , находящихся на расстоянии друг от друга, рассчитанная на отрезок проводника длиной , выражается формулой

• Магнитный момент контура с током

где – площадь, охватываемая контуром; – единичный вектор нормали к поверхности контура.

• Вращфающий момент сил, действующих на контур с током, помещенный в однородное магнитное поле

Модуль вектора :

где – угол между векторами и .

• Сила , действующая на заряд, движущийся со скоростью в магнитном поле с индукцией (сила Лоренца) выражается формулой

или

где – угол, образованный вектором скорости движения частицы и вектором индукции магнитного поля.

• Закон полного тока для тока проводимости: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура, охватывающего ток , выражается формулой

где – проекция вектора напряженности на направление касательной к контуру, содержащей элемент ; – сила тока, охватываемого контуром.

Если контур охватывает токов, то

где – алгебраическая сумма токов, охватываемых контуром.

• Магнитный поток через плоский контур площадью :

в случае однородного поля

или

где – угол между векторами нормали к плоскости контура и вектором магнитной индукции ; – проекция вектора на нормаль ();

в случае неоднородного поля

где интегрирование ведется по всей площади .

• Работа перемещения замкнутого контура с током в магнитном поле

где – изменение магнитного потока, пронизывающего поверхность, ограничен­ную контуром; – сила тока в контуре.

• Основной закон электромагнитной индукции (закон Фарадея-Максвелла)

где – электродвижущая сила индукции; – число витков контура.

Частные случаи применения основного закона электромагнитной индукции:

разность потенциалов на концах проводника длиной , движущегося со скоростью в однородном магнитном поле,

где – угол между направлениями векторов скорости и магнитной индукции ;

электродвижущая сила индукции , возникающая в рамке, содержащей витков, площадью , при вращении рамки с угловой скоростью в однородном магнитном поле с индукцией

где – мгновенное значение угла между вектором и вектором нормали в плоскости рамки.

• Электродвижущая сила самоиндукции , возникающая в замкнутом контуре при изменении силы тока в нем,

или

где – индуктивность контура.

• Индуктивность соленоида (тороида):

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнитной проницаемости следует пользоваться графиком зависимости от , а затем пользоваться формулой

• Мгновенное значение силы тока 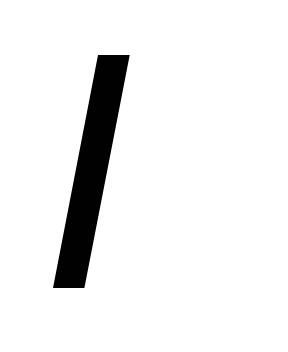в цепи, обладающей активным сопротивлением 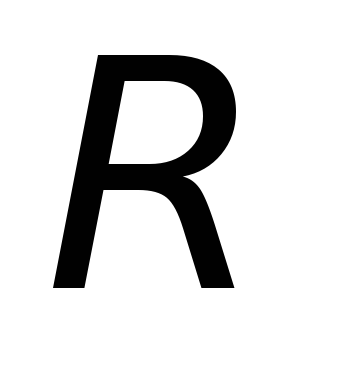и индуктивностью :

после замыкания цепи

после размыкания цепи

• Энергия 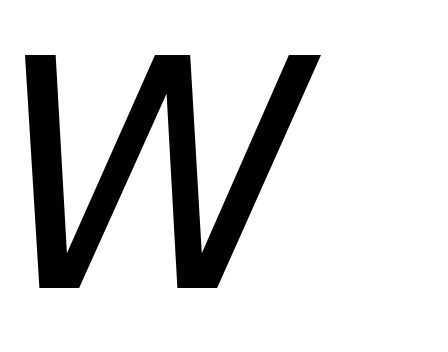магнитного поля, создаваемого током в замкнутом контуре индуктив­ностью 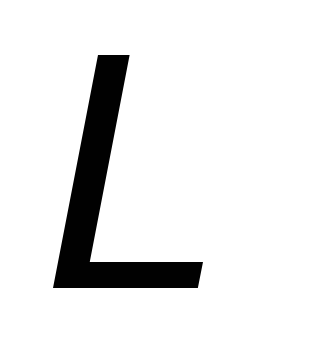определяется формулой

где – сила тока в контуре.

• Объемная (пространственная) плотность энергии однородного магнитного поля длинного соленоида

Волновая оптика

• Скорость света в среде

где – скорость света в вакууме; – абсолютный показатель преломления среды.

• Оптическая длина пути световой волны

где – геометрическая длина пути световой волны в среде с показателем преломления .

• Оптическая разность хода двух световых волн

• Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки находящейся в воздухе

или

где – толщина пластинки (пленки); – угол падения; – угол преломления.

• Связь разности фаз колебаний с оптической разностью хода световых волн

• Условие максимумов интенсивности света при интерференции

• Условие минимумов интенсивности света при интерференции

• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)

где – номер кольца ; – радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.

• Радиусы темных колец в отраженном свете (или светлых в проходящем)

• Радиус -й зоны Френеля

для сферической волны

где – расстояние диафрагмы с круглым отверстием от точечного источника света; – расстояние диафрагмы до экрана, на котором ведется наблюдение дифракционной картины; – номер зоны Френеля; – длина волны;

для плоской волны

• Дифракция света от одной щели при нормальном падении лучей. Условие минимумов интенсивности света

где – ширина щели; – угол дифракции; – номер минимума; – длина волны.

• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности

• Разрешающая сила дифракционной решетки

• Угловая дисперсия дифракционной решетки

линейная дисперсия дифракционной решетки

Для малых углов дифракции

где – главное фокусное расстояние линзы, собирающей на экране дифраги­рующие волны.

• Закон Брюстера