Лекция №3

(Буланчук О.Н., каф. физики ПГТУ )

Временное уравнение Шредингера1– основное уравнение квантовой механики.

Поскольку частицы обладали свойствами волн, то, по всей видимости, должно было бы существовать уравнение, которое описывает эти волны. Такое волновое уравнение было получено Шредингером в 1926 г. В отличие от основных уравнений механики и электромагнетизма основное уравнение квантовой механики было получено Шредингером эвристическим путем (из идеи Де Бройля и оптико-механической аналогии) и не является прямым обобщением опытных фактов. Это означает, что оно не может быть получено из эксперимента (поскольку главной величиной является волновая функция, которая, как оказалось впоследствии, не имеет физического смысла). Правильность уравнения впоследствии была подтверждена большим количеством опытов, результаты которых всегда находились в превосходном согласии с предсказаниями квантовой механики.

“Вывод” уравнения Шредингера.

Из уравнений Максвелла можно получить волновое уравнение для электромагнитных волн:

подставив в решение в виде плоской гармонической волны в и выполнив дифференцирование получим :

.

Выражение носит название дисперсионного уравнения. Таким образом, можно сделать вывод, что каждому дисперсному уравнению соответствует волновое и наоборот. Сопоставляя , и можно заметить, что частным производным соответствуют определенные множители в дисперсионном уравнении:

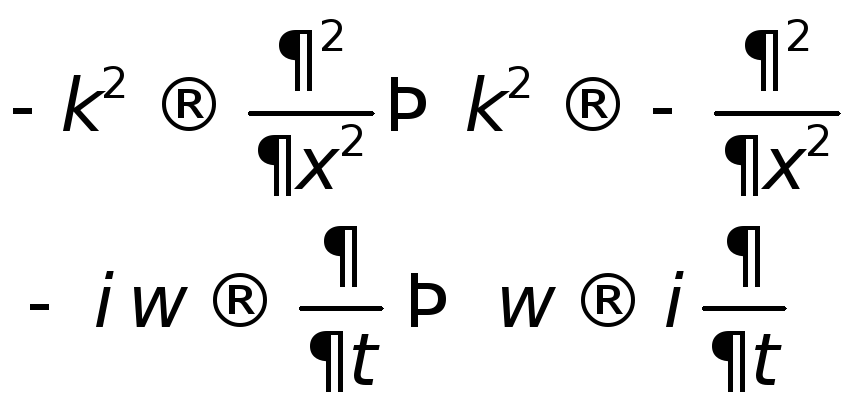
Для нахождения волнового уравнения волн Де Бройля вначале получим дисперсионное уравнение (в нерелятивистском случае):

Из с учетом восстановим волновое уравнение:

В трехмерном случае

,

где —оператор Лапласа в декартовой системе координат. Уравнения , являются временными (нестационарным) уравнением Шредингера в нерелятивистском случае. В входит волновая функция, смысл которой вначале не был вполне ясен (Шредингер надеялся, что введенная им волновая функция позволит устранить идею“квантовых скачков” и полагал, что она должна иметь физический смысл). Однако впоследствии выяснилось, что волновая функция связана с вероятностью обнаружить частицу в заданной области пространства, а волны Де Бройля стали называть волнами вероятности. С классической точки зрения это было необъяснимо, поскольку частицу, выпущенную из источника в определенном направлении, можно было обнаружить в различных местах фотопленки. Предсказать можно было только вероятность того, что частица попадет в заданную область.

Уравнение часто записывают в несколько другом виде:

,

где —оператор Гамильтона (или оператор полной механической энергии). Понятие “оператор” является ключевым в квантовой механике. Результатом действия оператора на функцию будет другая функция, но того же типа.

Волновая функция и ее физический смысл

Волновая функция – управляющая функция, которая сама по себе не имеет физического смысла. Правильную интерпретацию волновой функции дал М.Борн² в 1926 г. Физический смысл имеет , которая является мерой вероятности нахождения частицы в данном месте. С математической точки зрения —плотность вероятности найти частицу в момент временив точке с координатами. В общем случае является комплексной величиной. Почему вводится таким необычным образом? Ответ на этот вопрос следует из аналогии с оптикой.

Известно, что фотохимическое, биологическое и другие воздействия света на вещество обусловлены именно электрической компонентой поля. При этом, действие электромагнитного поля на вещество определяется интенсивностью волны (т. е., амплитудой волны в квадрате). С другой стороны, полагая, что свет является потоком фотонов, получим, что(– плотность потока фотонов: число фотонов, попадающих на единицу поверхности за единицу времени). Очевидно, что количество частиц, попадающих на некоторую поверхность, будет пропорционально вероятностипопадания частиц на данную поверхность. Таки образом получается следующая цепочка. Следовательно, вероятность пропорциональна амплитуде электромагнитной волны в квадрате. В случае волной функции для микрочастиц .

В физике в большинстве случаев используют частотное определение вероятности:

,

где —число испытаний в которых интересующей нас событие появилось (в данном случае число частиц попадающих в заданный объем или на поверхность),—общее число испытаний (полное число частиц). Плотность вероятности равна пределу отношения вероятности попаданиячастицы в объемв точке с координатамив момент временик величине этого объема:

Из видно, что плотность вероятности численно равна вероятности обнаружения частицы в единичном объеме заданной точки пространства в момент времени . Таким образом, зная, можно определить вероятность нахождения частицы в объемепо формуле

.

В одномерном случае — вероятность найти частицу в области пространства с координатами.

Следует подчеркнуть следующее:

1. в отличие от других физических величин не измеряется непосредственно в эксперименте;

2. не имеет определенной размерности и физического смысла;

Следовательно, имеем парадокс: рассчитываем величину, которая не измеряется. В связи с этим возникает вопрос: “Каким образом сопоставляются результаты квантовых расчетов с экспериментальными данными?”. Кроме возможности расчета вероятности в квантовой механике существует метод, позволяющий производить вычисления средних значений физических величин: каждой физической величине (по определенной методике) сопоставляется оператор. Например,

Тогда среднее значения физической величины вычисляются по формуле

.

Таким образом, уравнение Шредингера в квантовой механике играет роль второго закона Ньютона и закона сохранения полной механической энергии в классической физике. Оно позволяет предсказывать будущее динамической системы путем расчета вероятностей событий и результатов.