Лекция №7

(Буланчук О.Н., каф. физики ПГТУ )

Опыты Штерна и Герлаха. Спин электрона.

При движении электрона (как заряженной частицы) вокруг ядра он создает некоторый электрический ток. Этот ток (а также аналогичные токи в молекулах) получил название молекулярного тока. Однако если существует электрический ток, то в соответствии с законом Био-Саварра-Лапласа он должен создавать в окружающем пространстве магнитное поле, величина которого определяется магнитным моментом тока. Покажем, что магнитный момент электрона в атоме связан с его механическим моментом (орбитальным моментом импульса).

Будем полагать, что электрон движется по окружности. Тогда сила тока в атоме: магнитный момент по определению равен. Частота вращения электронамомент импульса для круговой орбиты. Отношение магнитного момента к механическому будет равно:

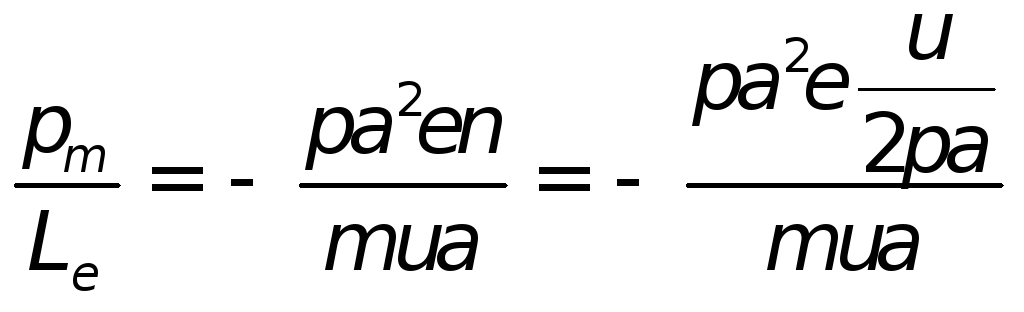
—гиромагнитное соотношение

Таким образом, орбитальный магнитый и механический момент оказываются связаны соотношением:

С учетом того, что проекция механического момента на выделенное направление из получим:

,

где —магнетон Бора. Т.е., проекция магнитного момента оказывается кратной магнетону Бора.

Если механический момент равен нулю, то и магнитный момент также равен нулю (). В 1921 Штерн и Герлах поставили опыты, в которых измерялся магнитный (а значит механический) момент атома (точнее электронов в атоме). Опыты Штерна и Герлаха относятся к числу основополагающих экспериментов атомной физики. Идея опыта: по величине расщепления пучка, проходящего между полюсами постоянного магнита, определялась сила, действующая на атом в неоднородном магнитном поле. Затем по величине силы рассчитывался магнитный момент атома. С помощью такой методики удалось экспериментально подтвердить существование магнитных моментов у атомов и их пространственное квантование.

В одномерном случае

.

Для наблюдения эффекта необходимо, чтобы неоднородность поля была достаточно велика на расстояниях порядка размеров атома. Для этого северный полюс магнита был изготовлен в виде призмы с острым ребром вдоль направления пучка, а в южном была проточена канавка в том же направлении. Если пропускать между магнитными полюсами атомы водорода (или другие атомы с одним валентным электроном всостоянии) в основном состоянии для которых, то в этом случае из следует чтои на экране должна была наблюдаться одна полоса. На самом деле оказалось две.

При этом расчеты показали, что магнитный момент оказался в два раза больше, чем определяемый по формуле . С точки зрения классической физики такой результат был невозможен. Объяснение опыта было предложено в 1925г. Гаудсмитом и Уленбеком, которые предположили наличие у электрона собственного магнитного и механического момента – спина. Спин можно представить как свойство электрона (заряженного шарика) вращающегося вокруг своей оси подобно волчку. Однако такая простая модель в данном случае оказывается неправильной. Зная магнитный, а значит и механический момент электрона можно, используя формулу (где–момент инерции электрона-шарика), рассчитать угловую и линейную скорость вращения электрона вокруг оси. При этом оказывается, что скорость вращения поверхности электрона в 300 раз больше скорости света, что противоречит специальной теории относительности. Это означает, что спин – внутреннее свойство электрона (и других элементарных частиц), например, такое же как заряд и масса, которому нельзя сопоставить классического аналога.

Результаты измерений показали, что спин электрона равен

,

где — спиновое магнитное квантовое число:.

.

–cпиновое квантовое число,

Таким образом, волновая функция электрона в атоме водрода должна зависеть от 4-х квантовых чисел: . В простейшем случае ее можно представить в виде, где—спиновая волновая функция. Кратность вырождения в этом случае увеличивается в два раза.

Для фотона . С понятием спина связано понятие спиральности частиц—знака проекции спина на направление импульса.

Замечание: спин электрона является релятивистским свойством. Дирак показал, что существование спина является следствием учета релятивистских эффектов в уравнении Шредингера (релятивистское волновое уравнения Дирака).

Учёные из Национального института стандартов США (NIST) создали микроскопический осциллятор, который может использоваться в мобильных телефонах, устройствах беспроводной связи и радарах. Отличие нового прибора в том, что его габариты в сотни раз меньше существующих устройств и сравнимы с толщиной человеческого волоса.

Новый осциллятор может генерировать электрические колебания с частотой от 5 до 40 гигагерц. Принцип его действия основан на периодическом изменении спина электронов в магнитных плёнках, разделённых слоем диамагнетика. Процесс происходит автоматически, частота колебаний зависит от величины протекающего по плёнкам тока.

Активная область экспериментального прибора, построенного учёными из NIST, имеет площадь в несколько квадратных микрон. Осциллятор очень недорог и прост в изготовлении, так что в ближайшем будущем можно ожидать революции в области беспроводных коммуникаций.