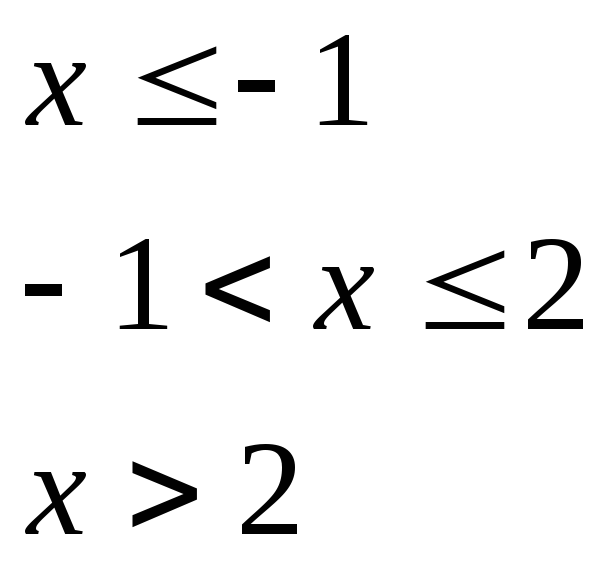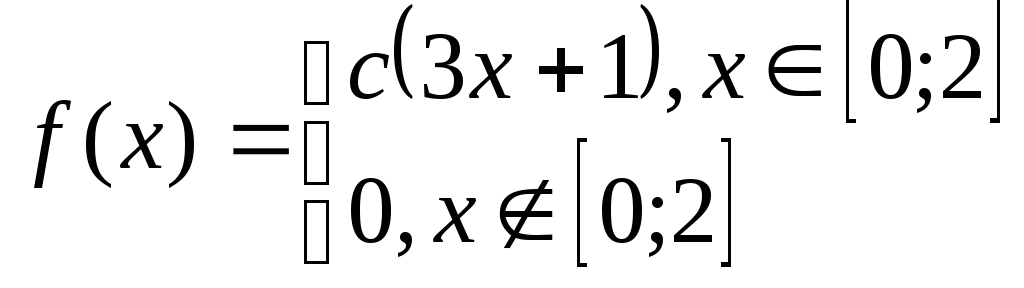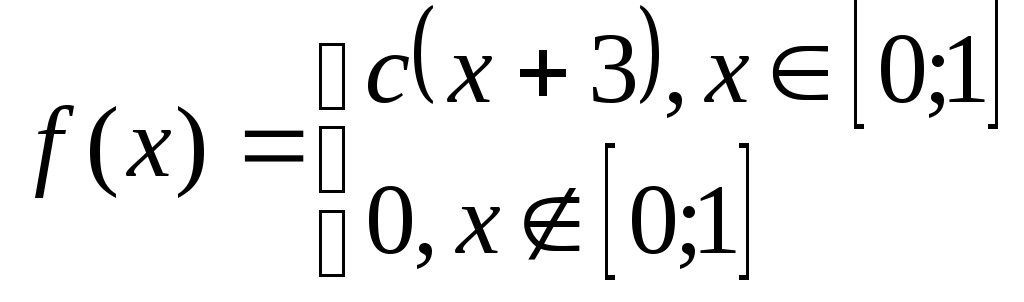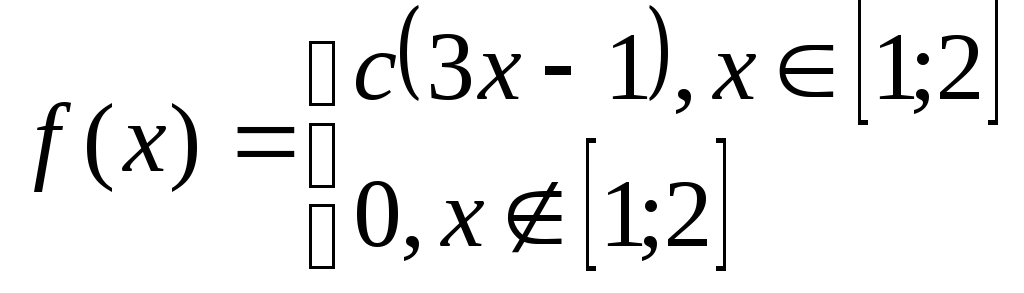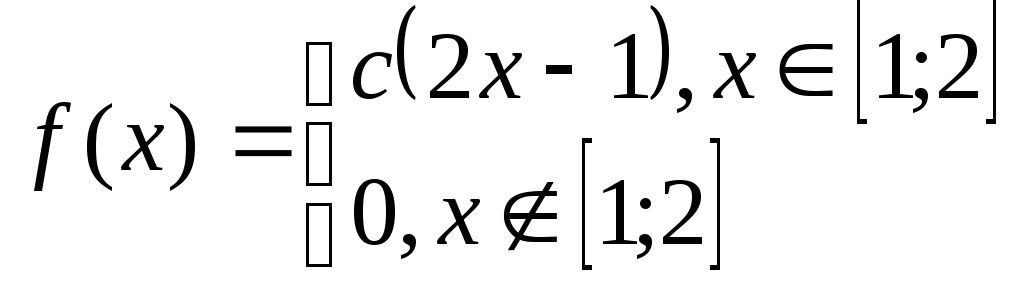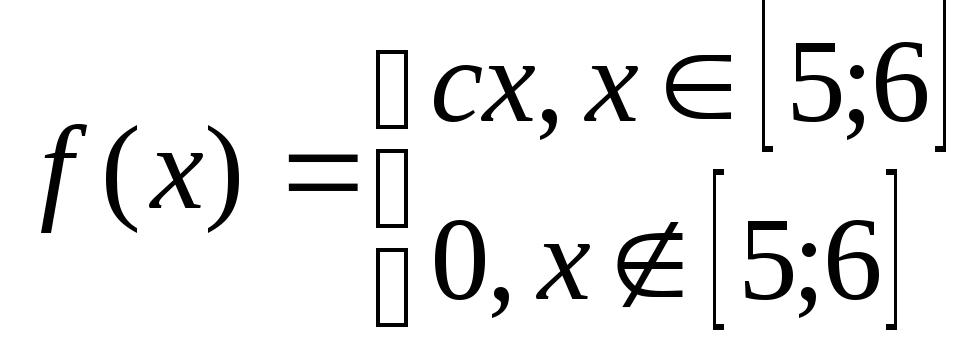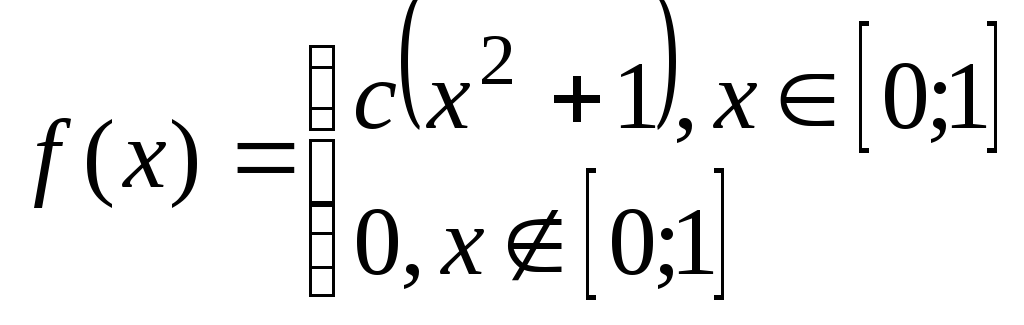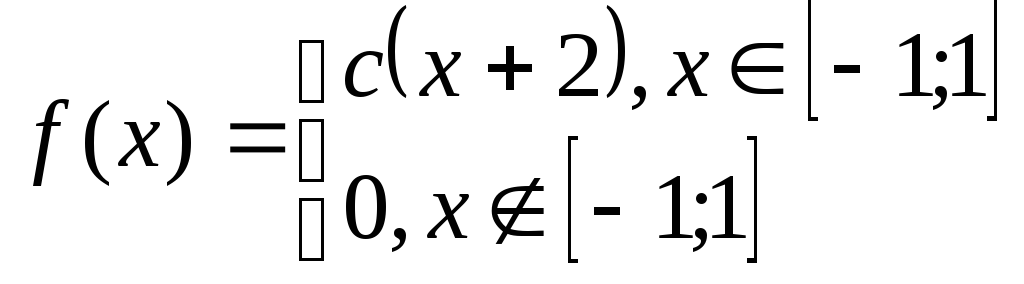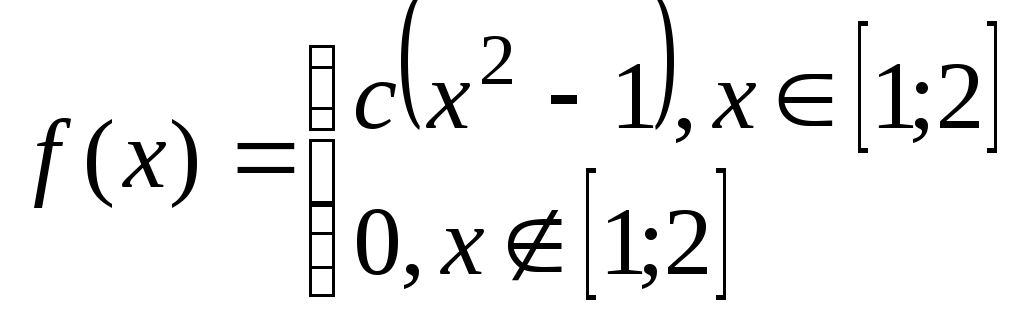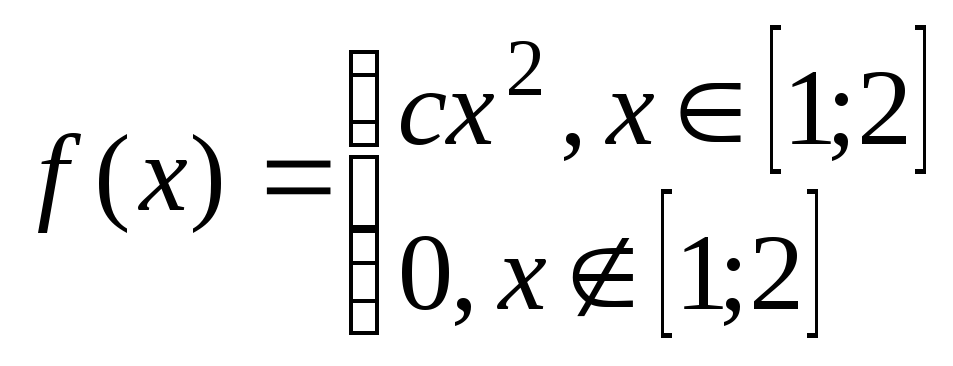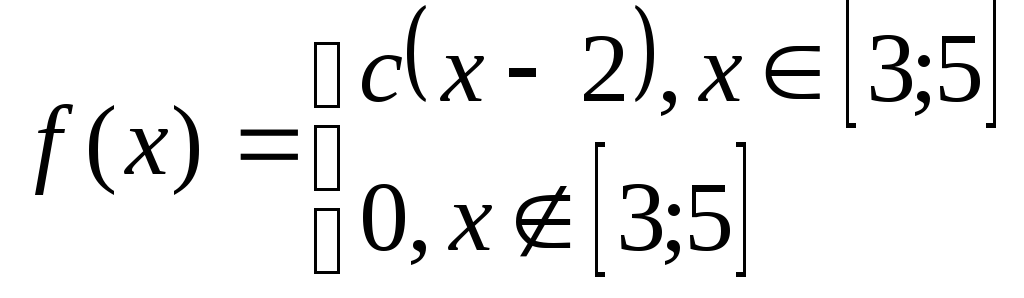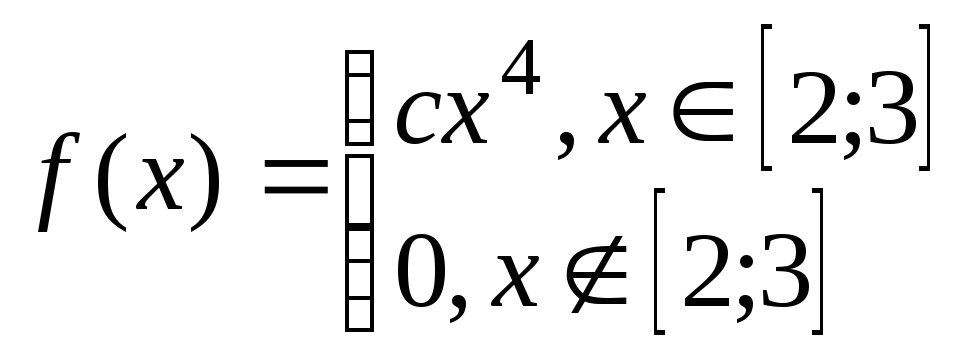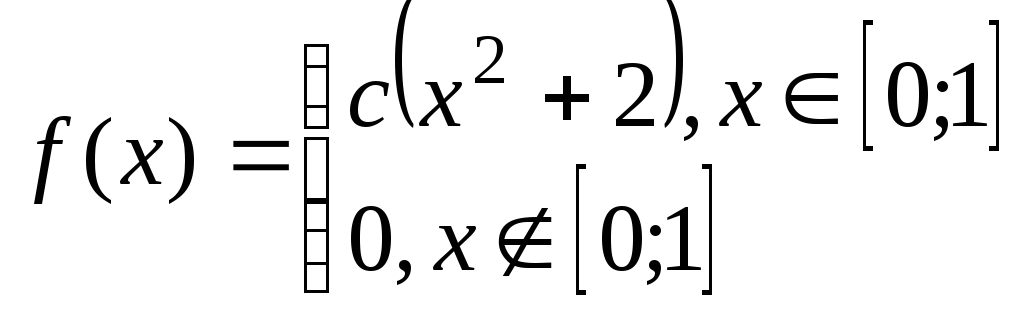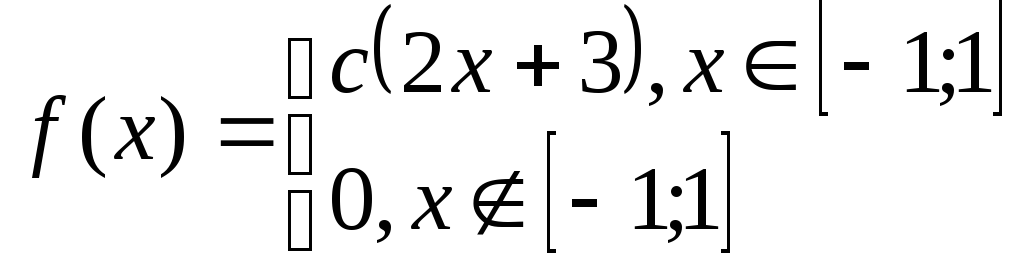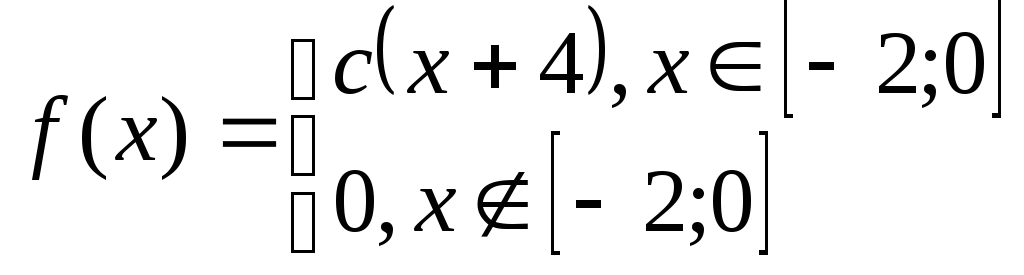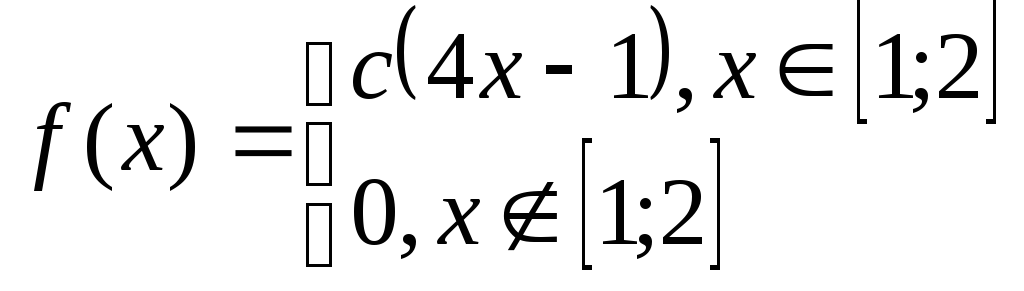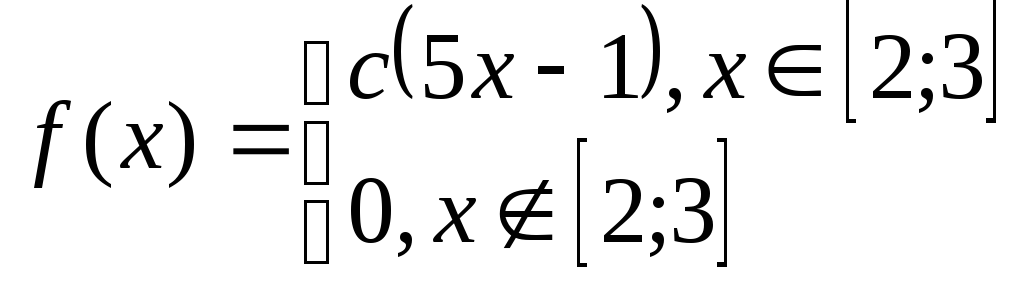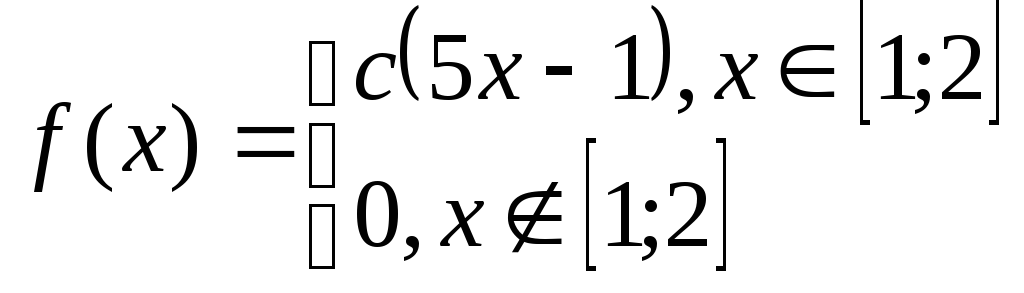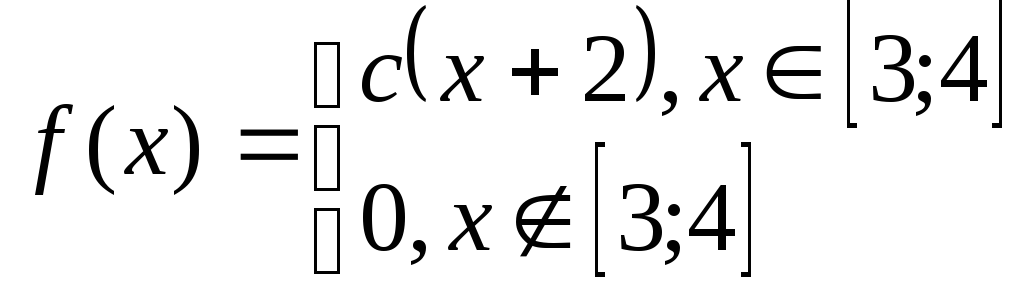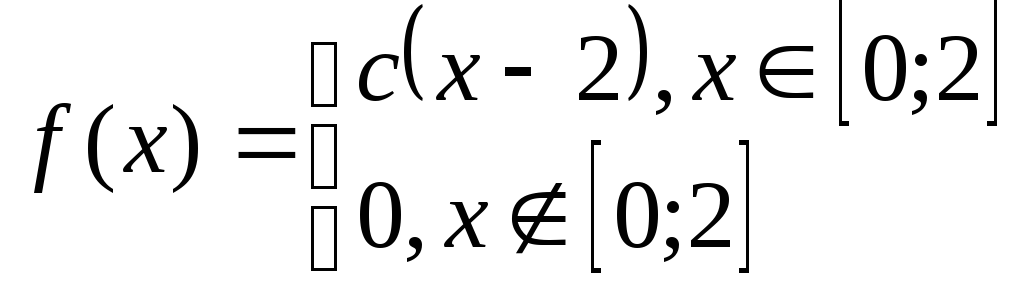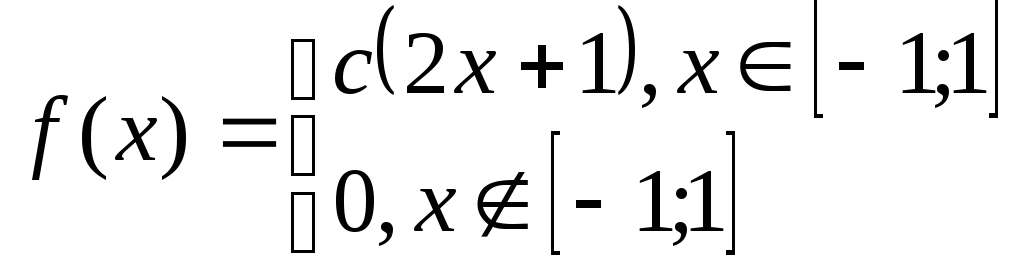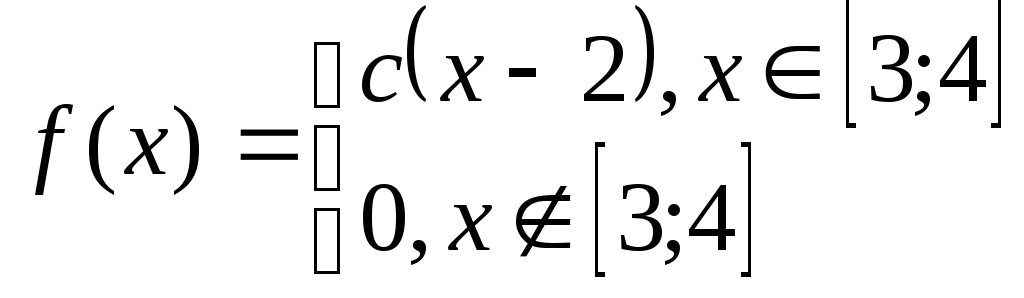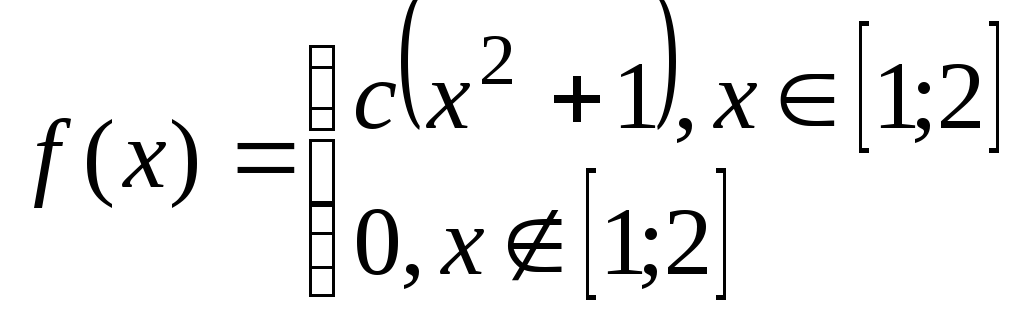- •Задания для самостоятельной работы
- •Задача №2. Теоремы сложения и умножения вероятностей.
- •Задача №3. Формула полной вероятности. Формулы Бейеса.
- •Задача №4. Предельные теоремы в схеме Бернулли.
- •Задача №5.1 Дискретные случайные величины.
- •Задача №5.2. Дискретные случайные величины.
- •Задача №6.1 Непрерывные случайные величины.
- •Задача№6.2 Непрерывные случайные величины.
- •Математическая статистика. Задача №7
- •Задача №8
- •Литература
Задача №5.2. Дискретные случайные величины.
В
ящике находится
![]() шаров, из которых
шаров, из которых![]() -
белые. Наудачу извлекаются 3 шара.
-
белые. Наудачу извлекаются 3 шара.
а). Найти закон распределения случайной величины Х – количества белых шаров среди извлечённых.
б). Построить многоугольник распределения.
в). Найти функцию распределения случайной величины Х и построить её график.
г). Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.
Исходные данные приведены в таблице.
-
№
1
11
3
2
7
4
3
8
5
4
9
3
5
10
4
6
6
5
7
7
3
8
8
6
9
9
5
10
10
6
11
6
4
12
7
5
13
8
4
14
9
4
15
10
5
16
6
3
17
7
4
18
8
5
19
9
6
20
10
7
21
7
3
22
8
4
23
9
5
24
10
3
25
8
4
26
11
5
27
9
3
28
11
4
29
7
5
30
8
3
Задача №6.1 Непрерывные случайные величины.
Случайная
величина задана интегральной функцией
распределения
![]() .
Определить:
.
Определить:
1) дифференциальную
функцию
![]() ;
;
2) математическое ожидание и дисперсию случайной величины Х;
3). построить
графики
![]() и
и![]() .
.
|
№ |
Интегральная
функция
|
№ |
Интегральная
функция
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
Задача№6.2 Непрерывные случайные величины.
Дана плотность распределения случайной величины Х. Определить:
коэффициент с;
функцию распределения F(x);
математическое ожидание М(х);
дисперсию D(x);
среднее квадратическое отклонение
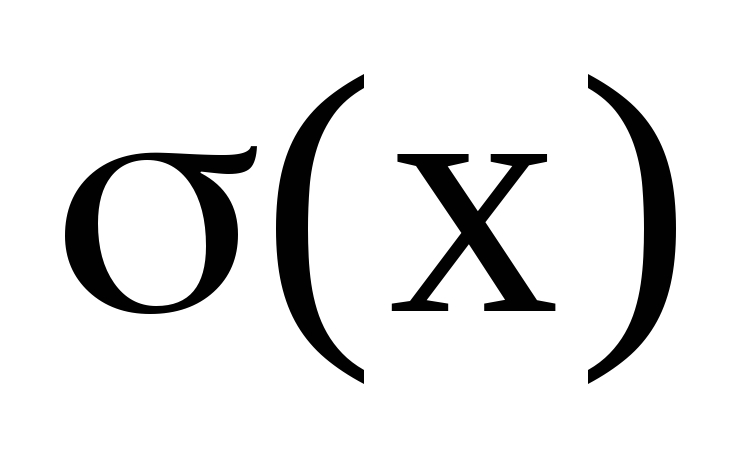 ;
;построить графики F(x) и f(x).
|
№ |
|
№ |
|
|
1 |
|
13 |
|
|
2 |
|
14 |
|
|
3 |
|
15 |
|
|
4 |
|
16 |
|
|
5 |
|
17 |
|
|
6 |
|
18 |
|
|
7 |
|
19 |
|
|
8 |
|
20 |
|
|
9 |
|
21 |
|
|
10 |
|
22 |
|
|
11 |
|
23 |
|
|
12 |
|
24 |
|

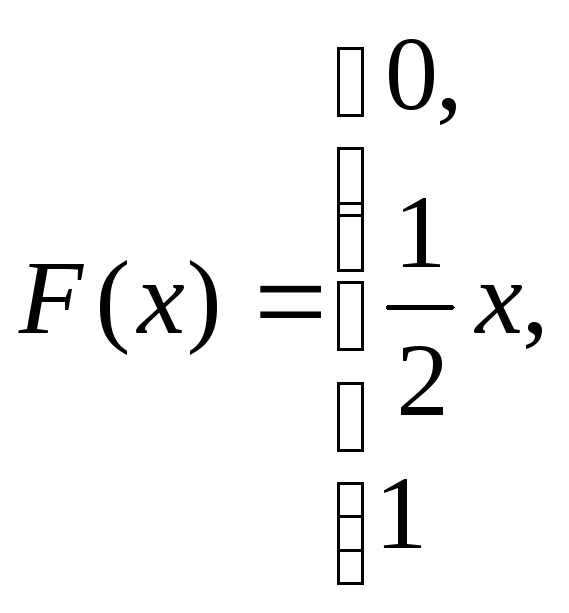 при
при 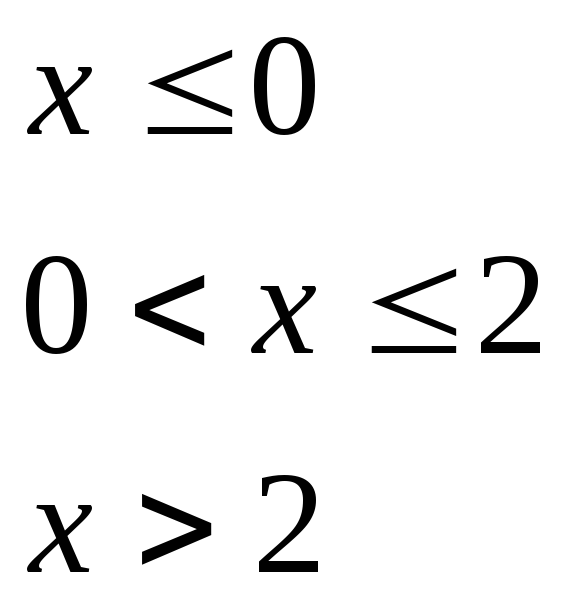
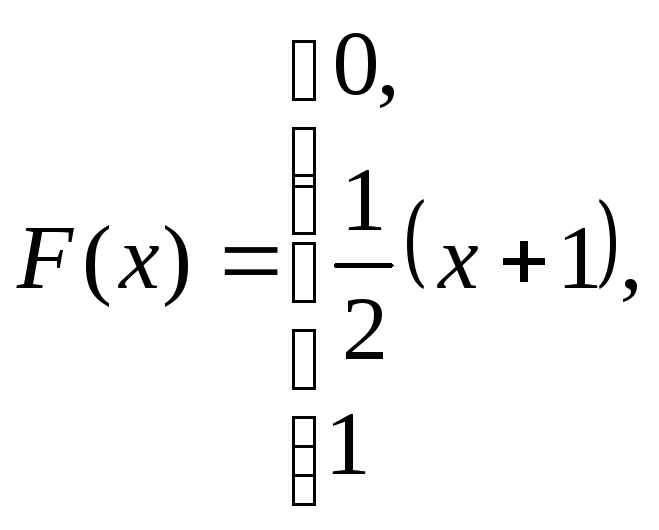 при
при 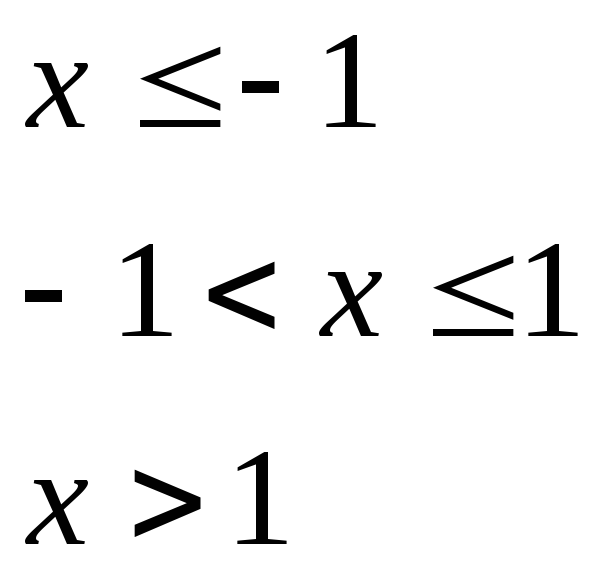
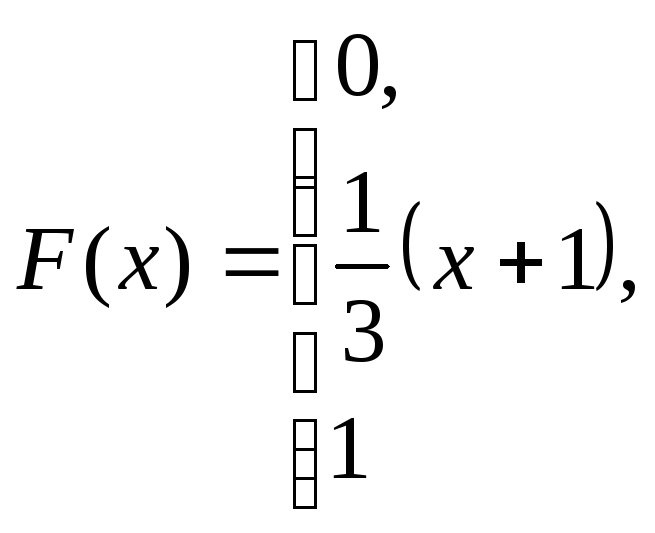 при
при 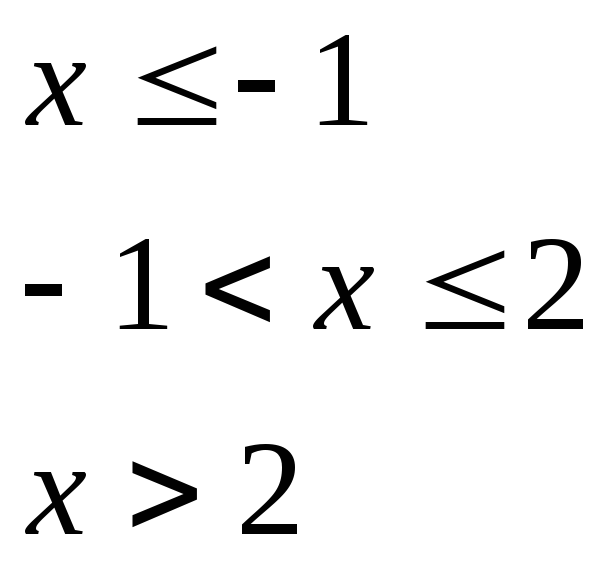
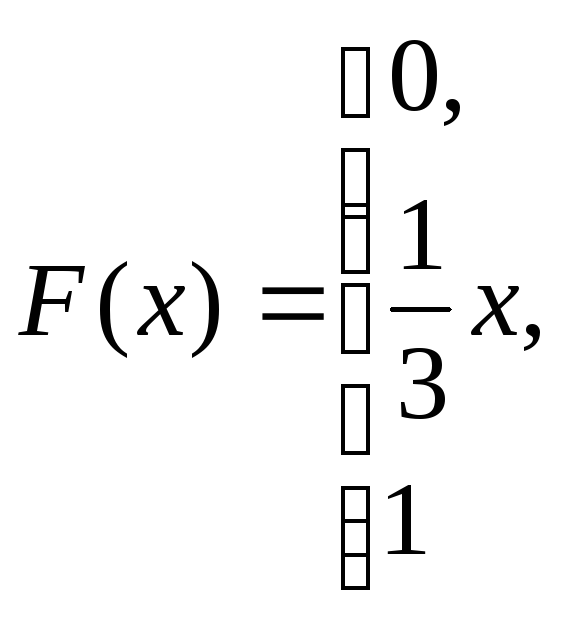 при
при 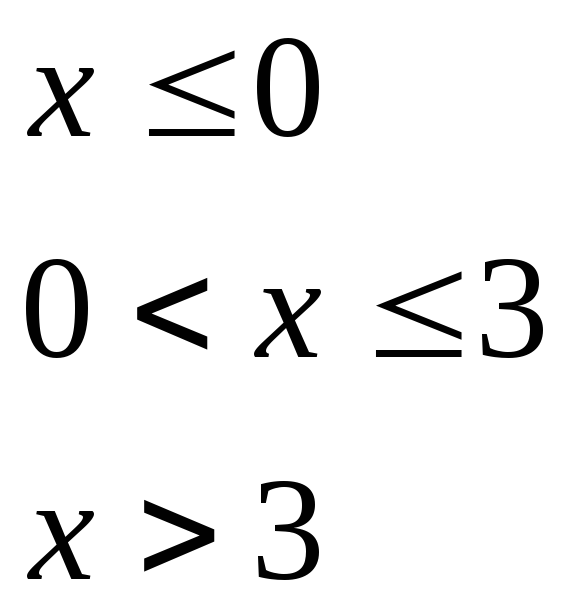
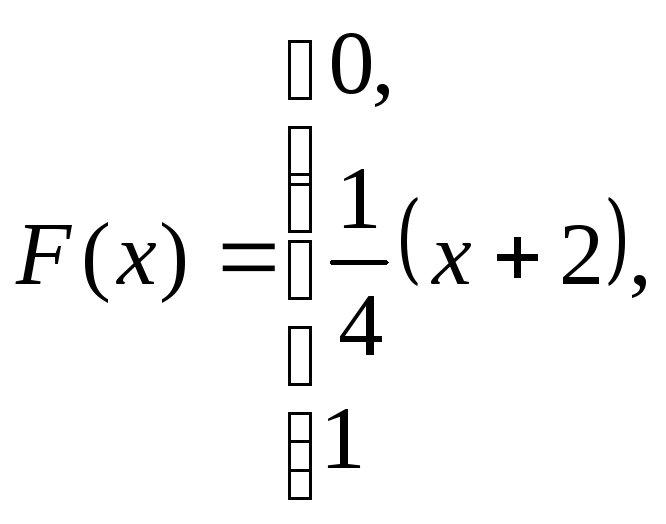 при
при 
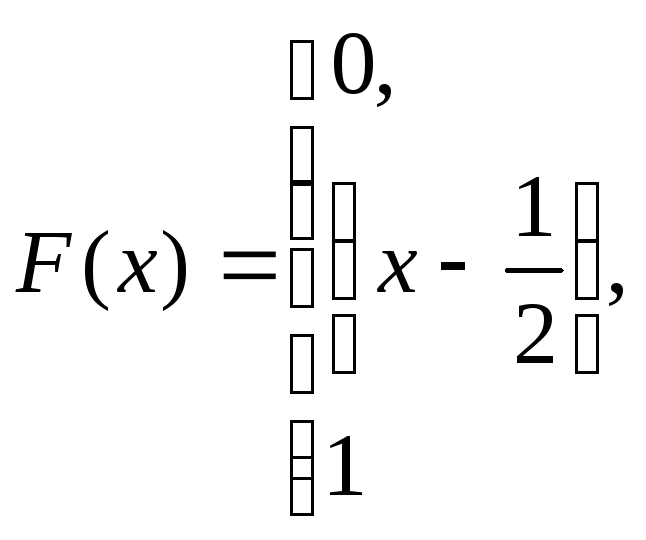 при
при 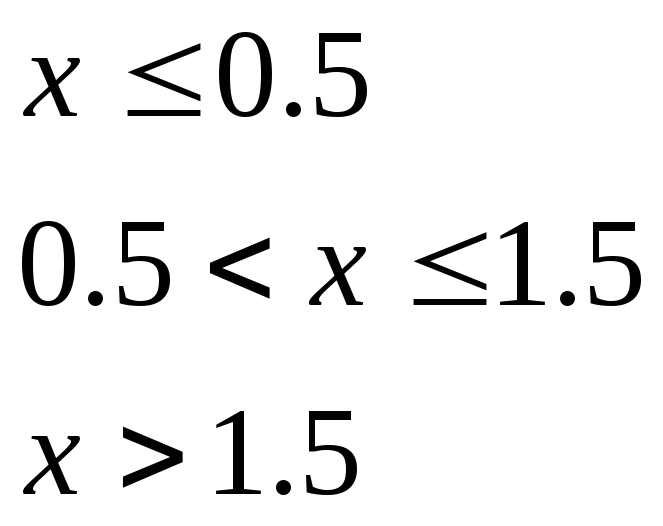
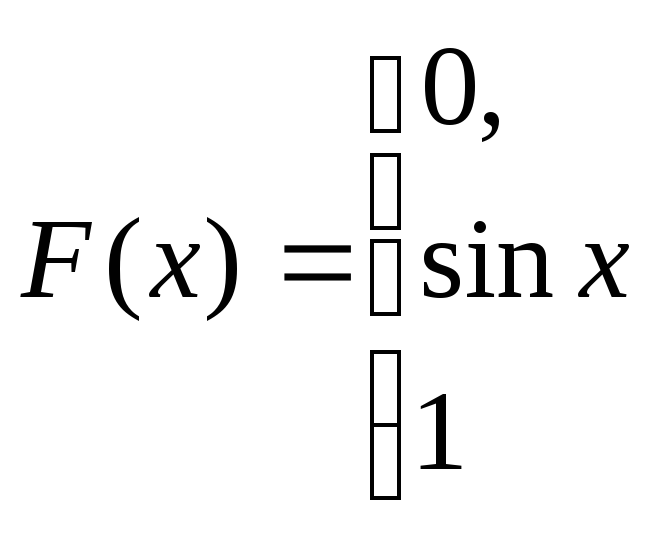 ,
при
,
при 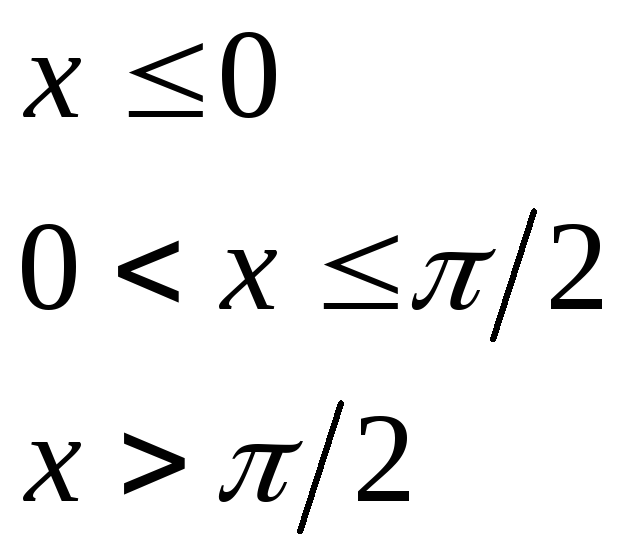
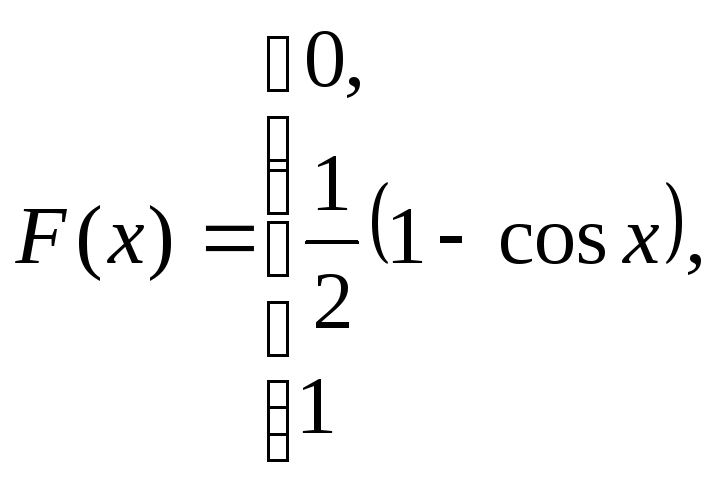 при
при 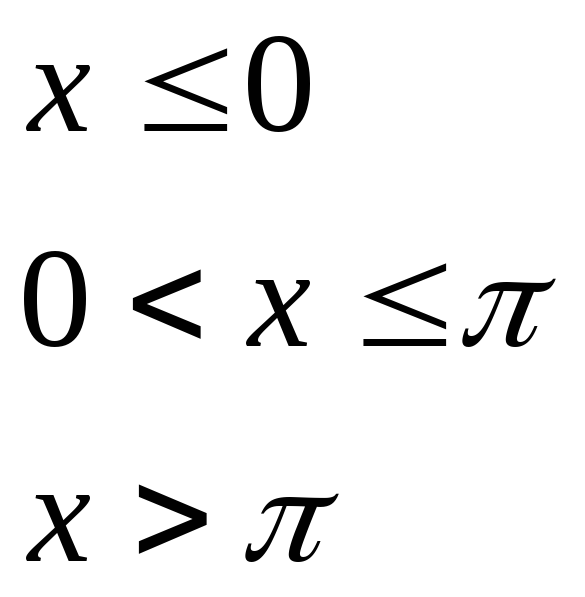
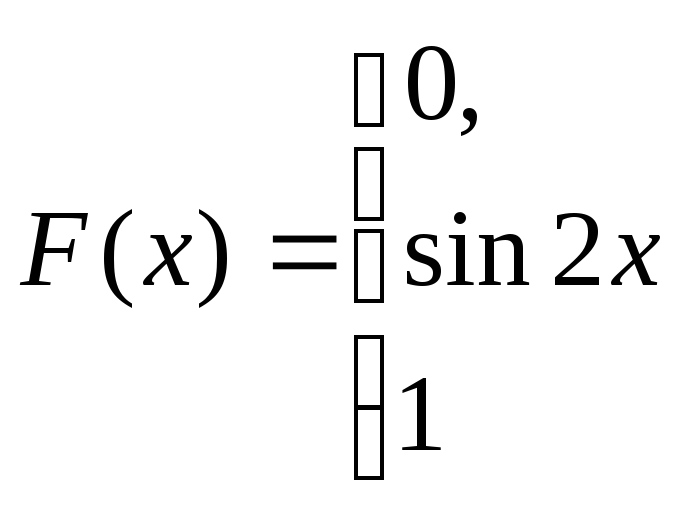 ,
при
,
при 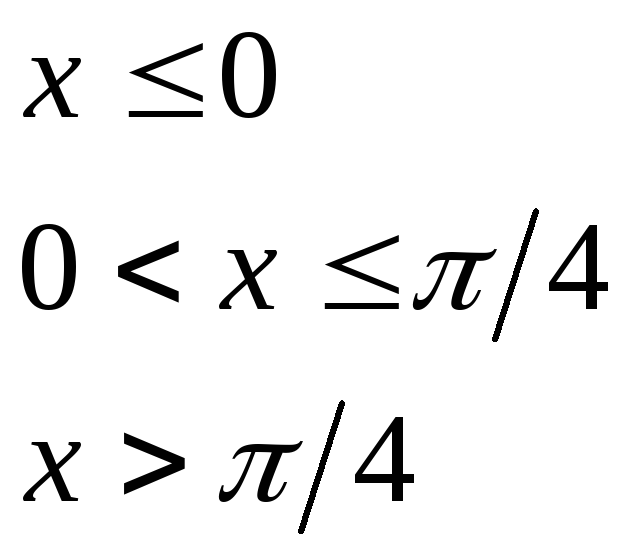
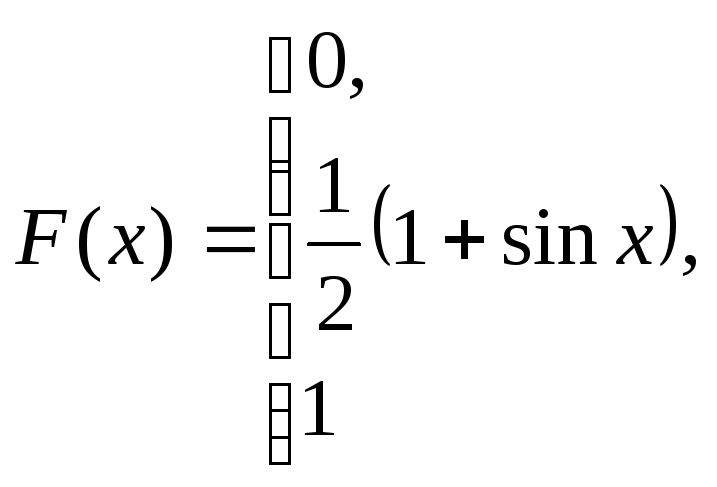 при
при
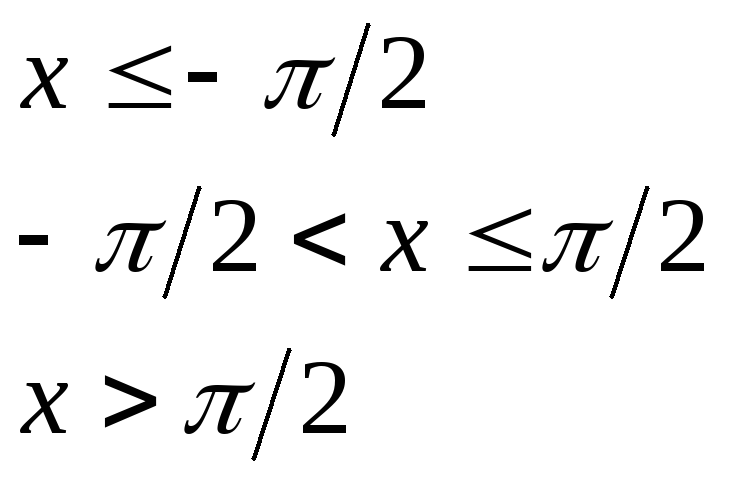
 при
при 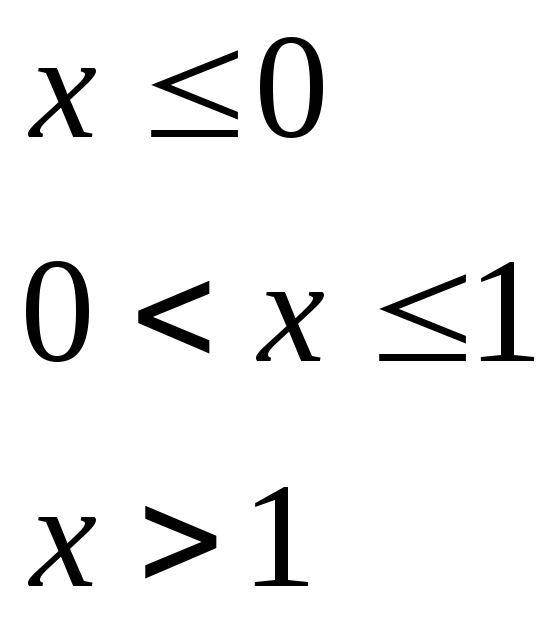
 при
при 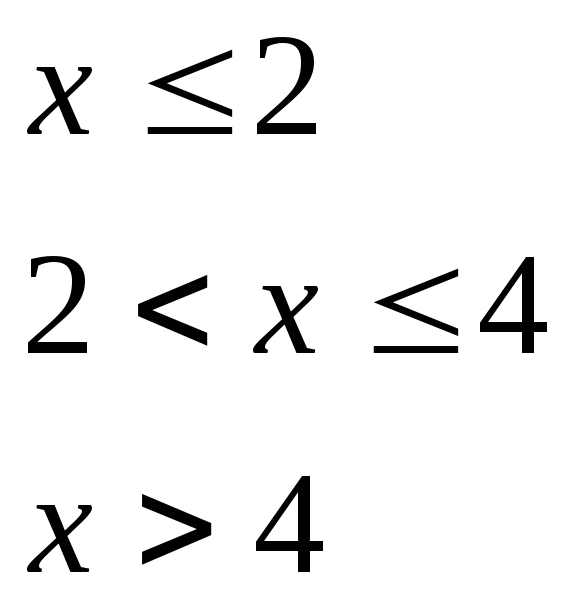
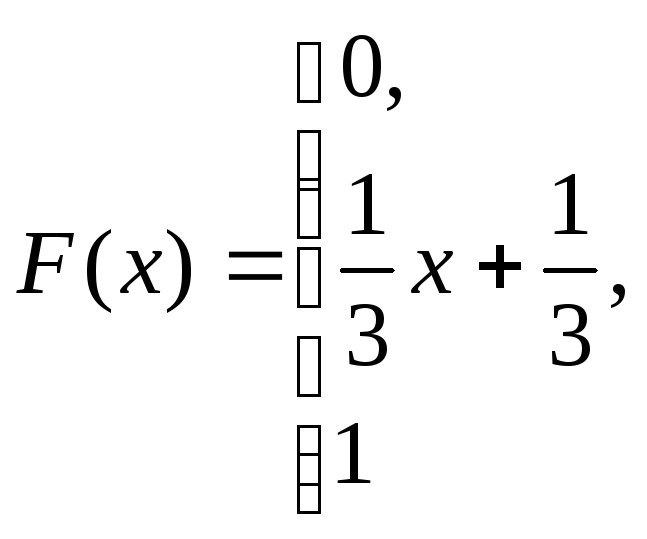 при
при 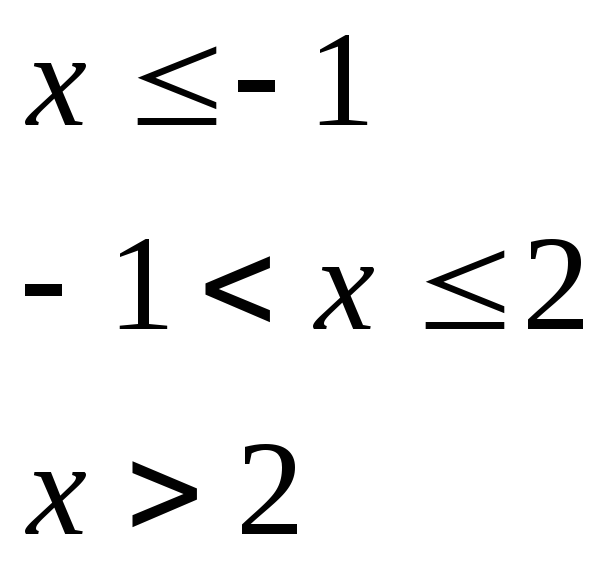
 при
при 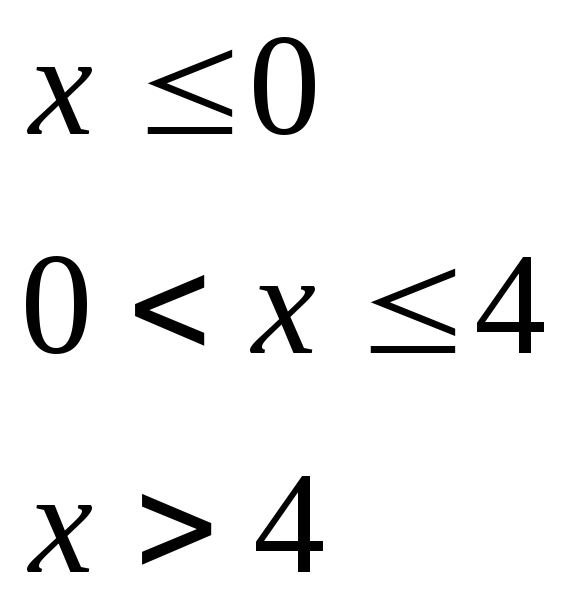
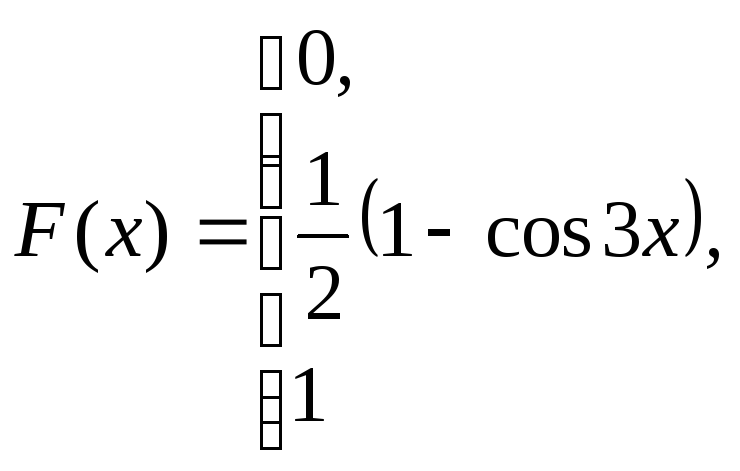 при
при
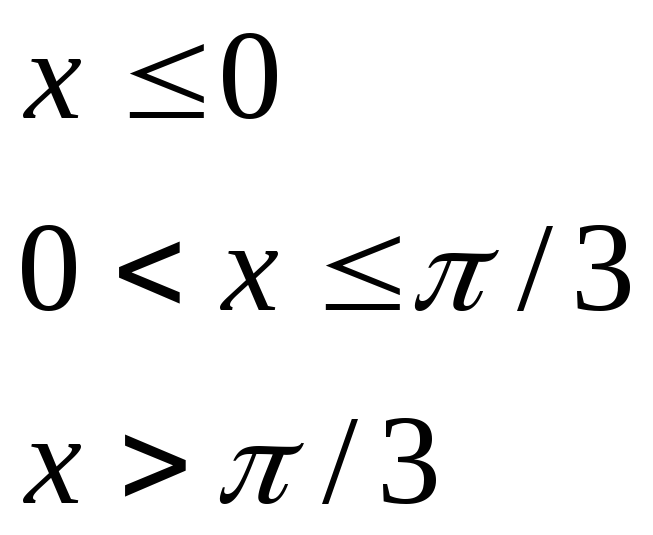
 при
при 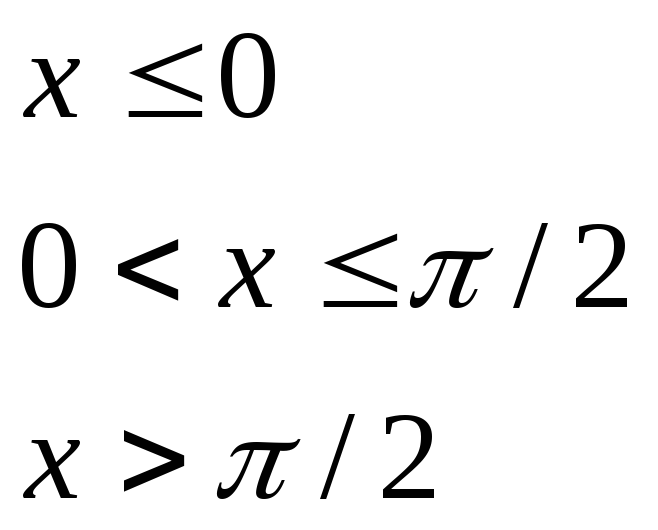
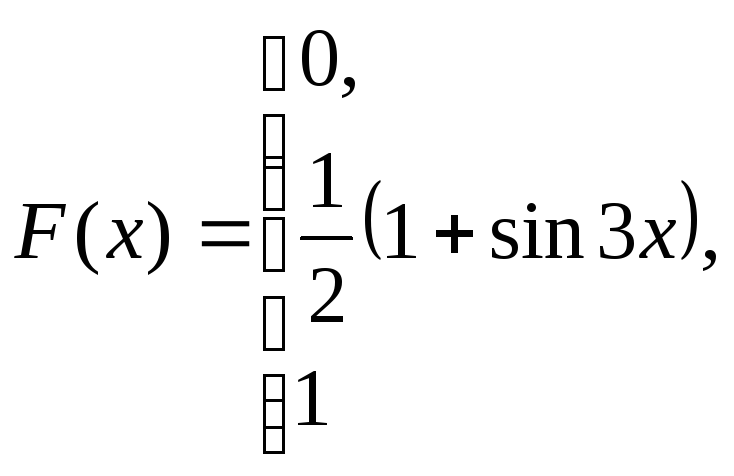 при
при
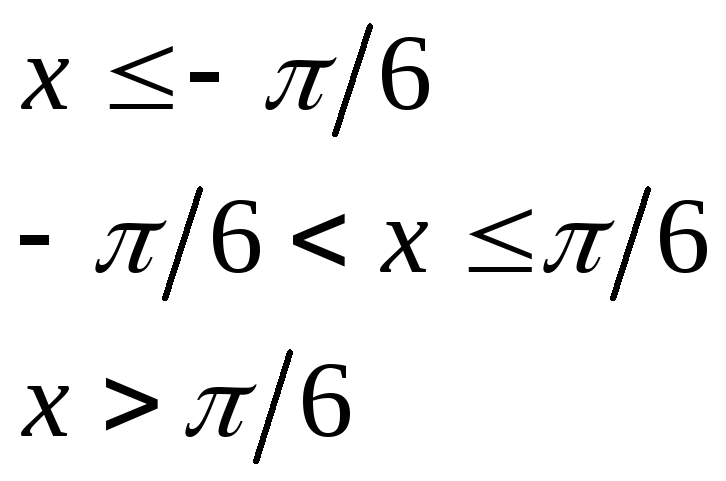
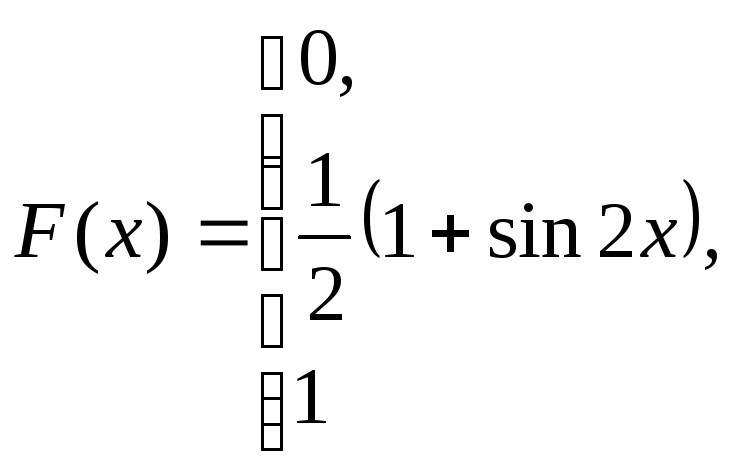 при
при
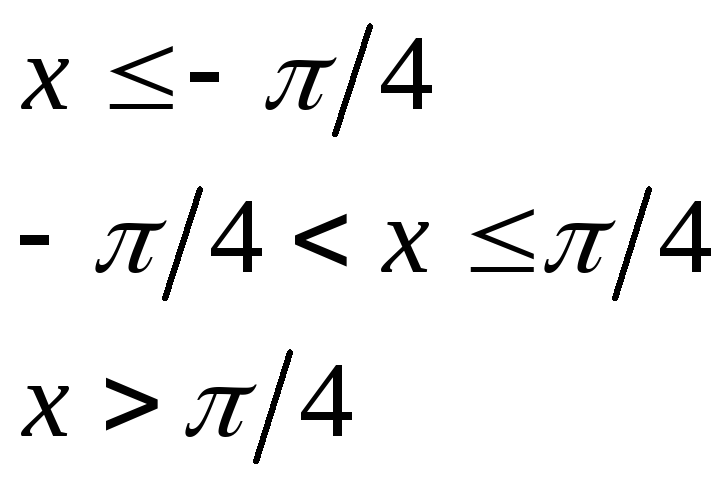
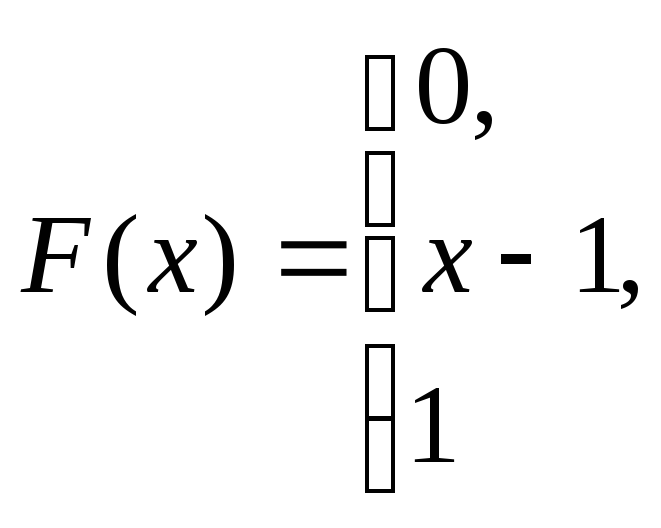 при
при 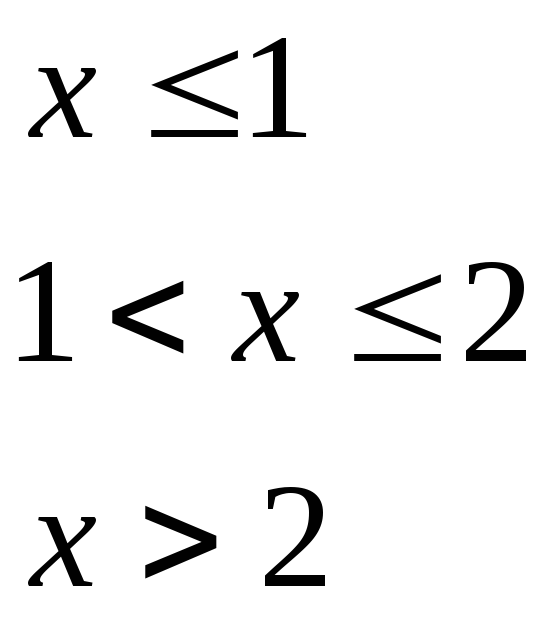
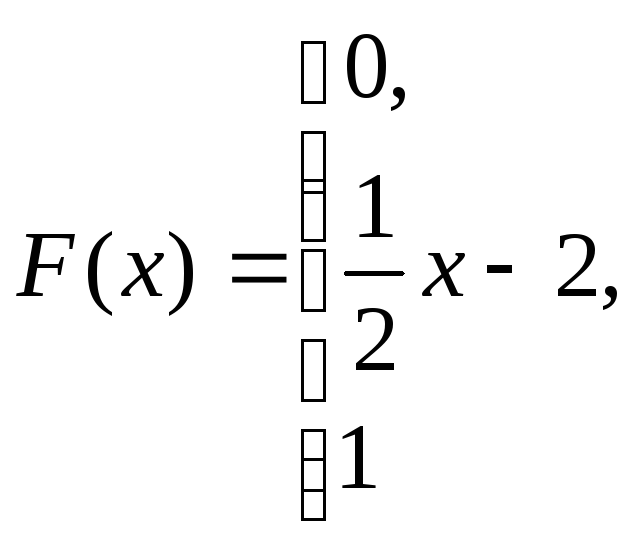 при
при 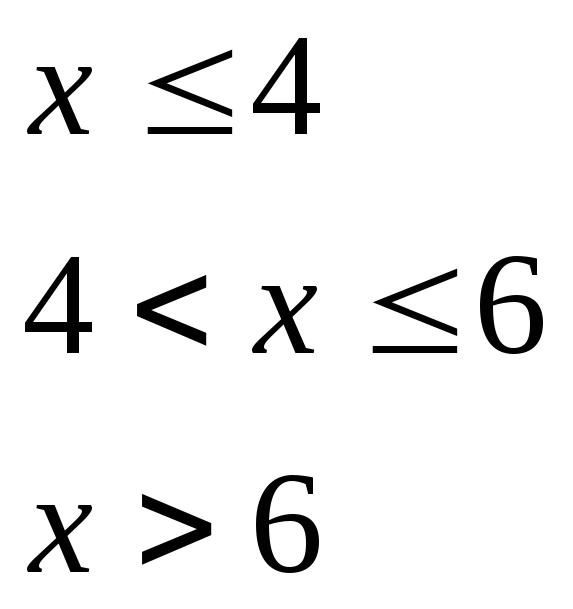
 при
при 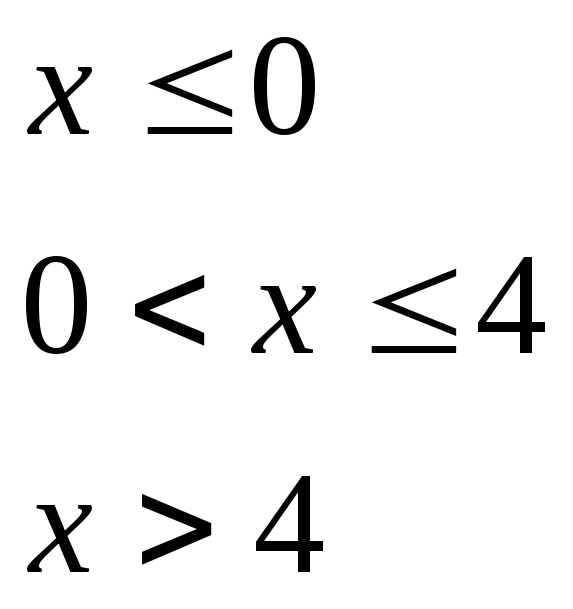
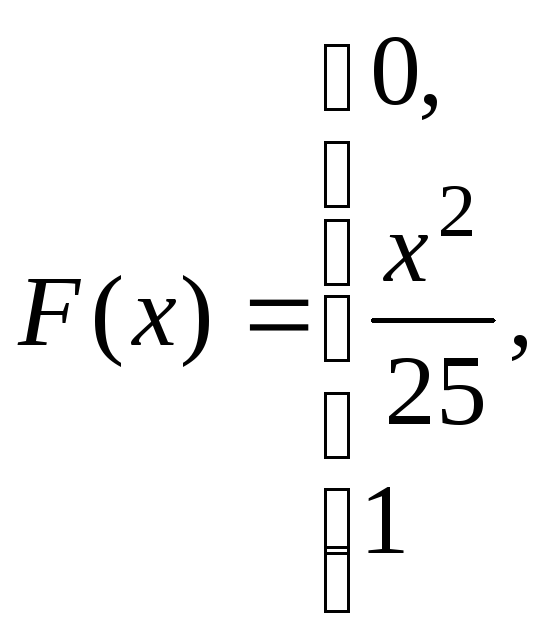 при
при 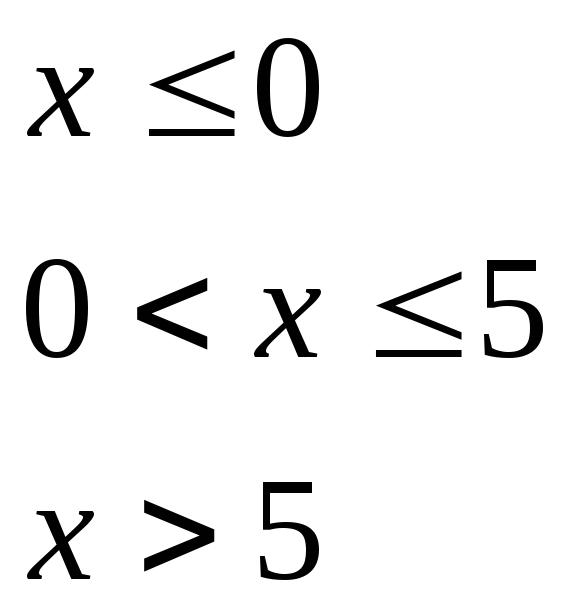
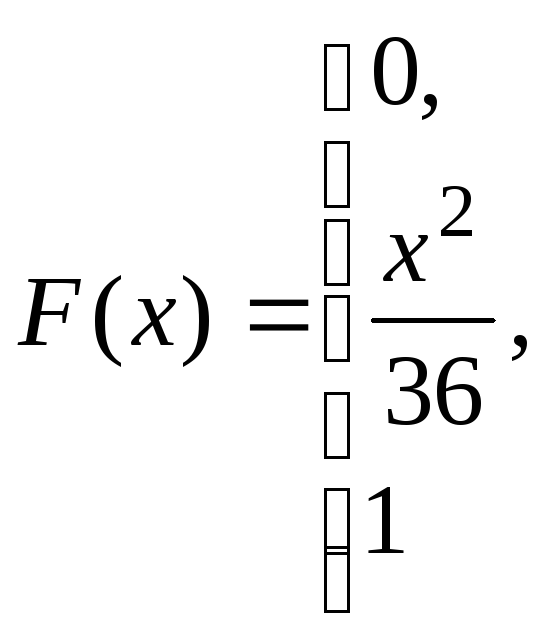 при
при 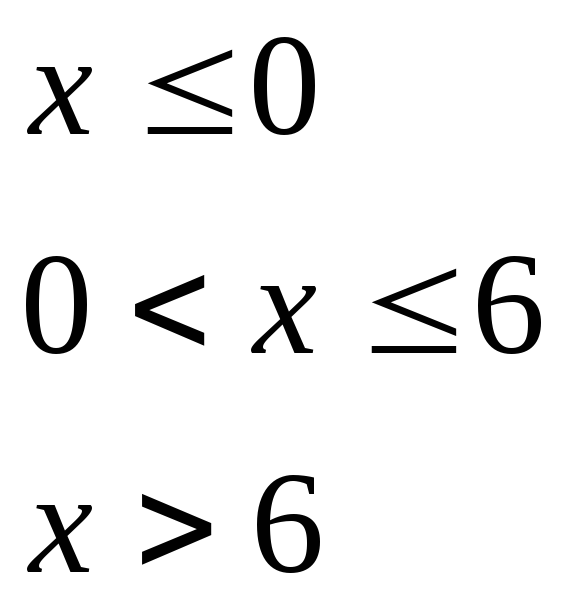
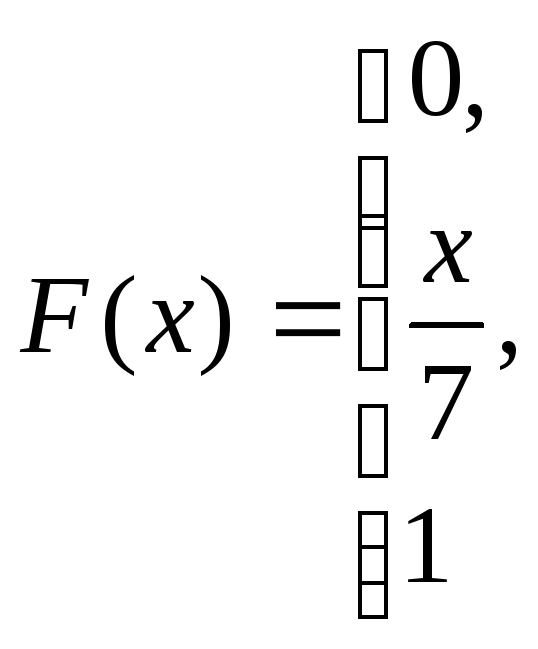 при
при 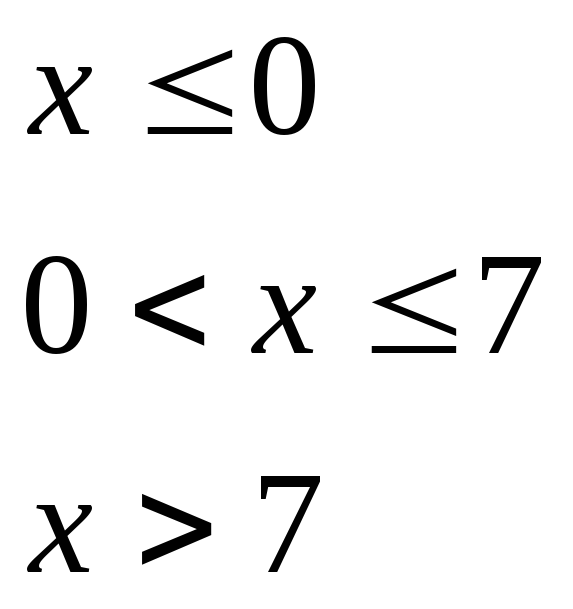
 при
при 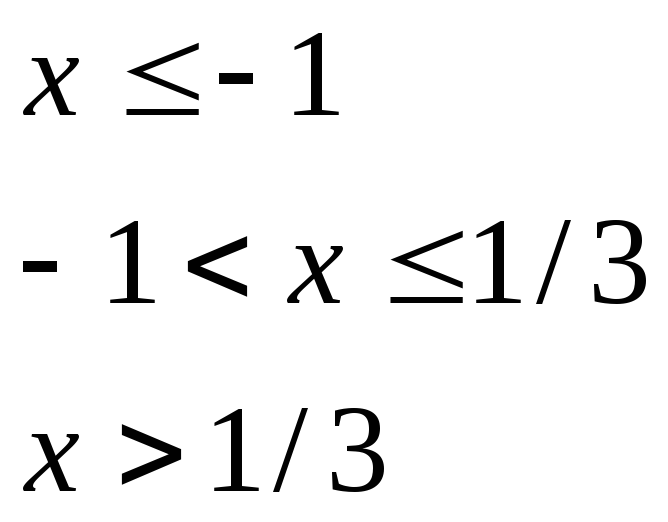
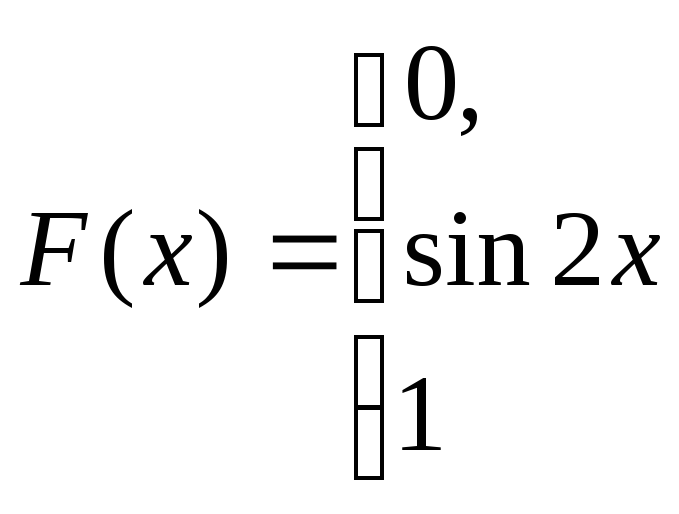 ,
при
,
при 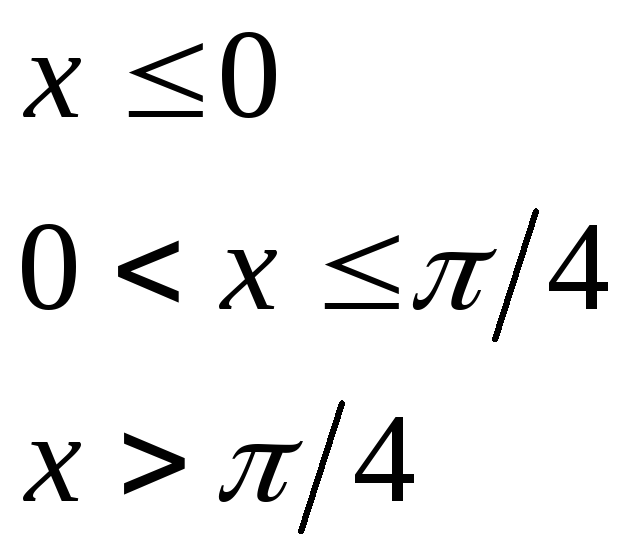
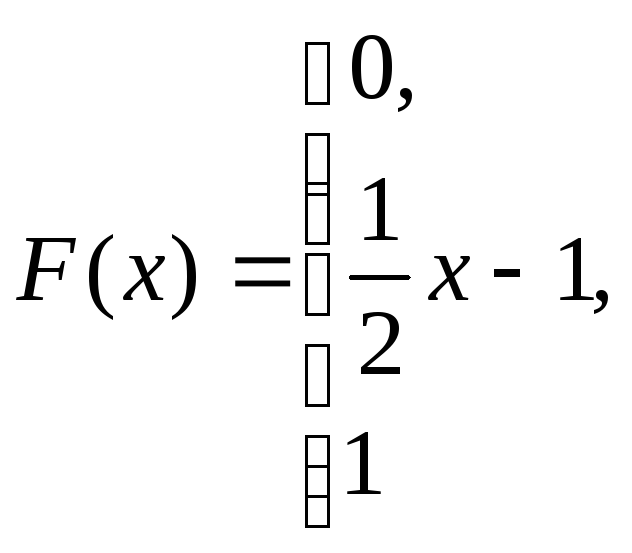 при
при 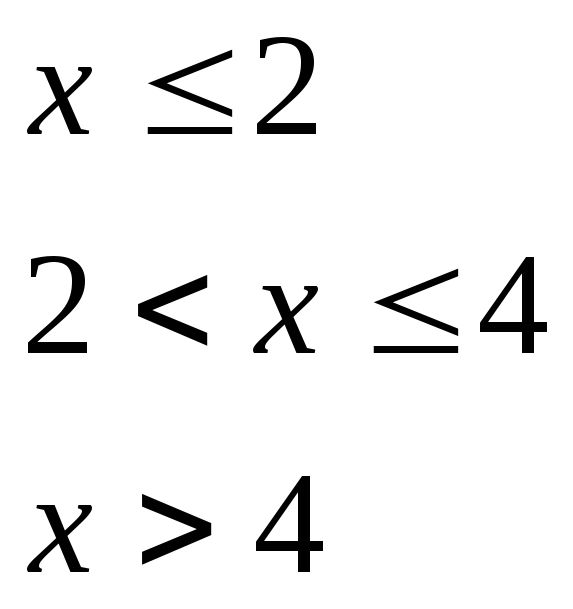
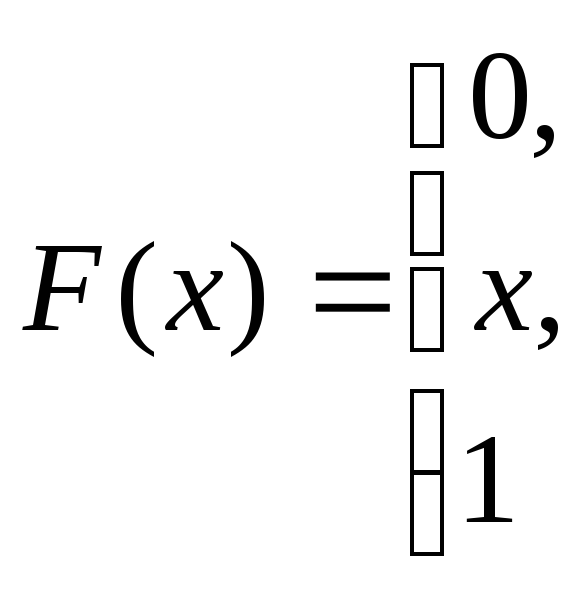 при
при 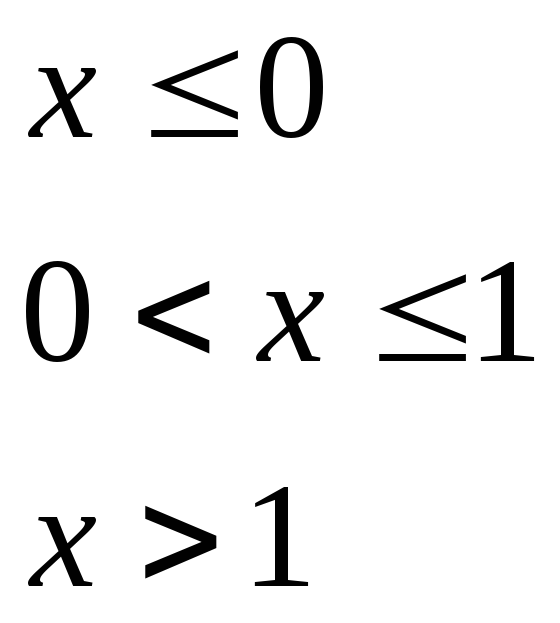
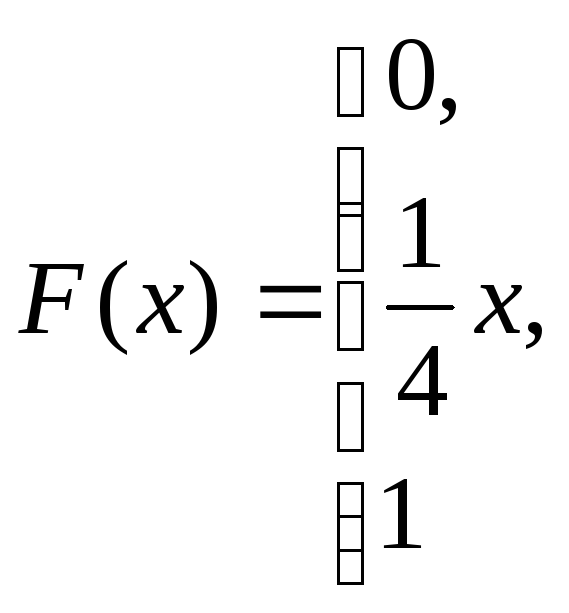 при
при 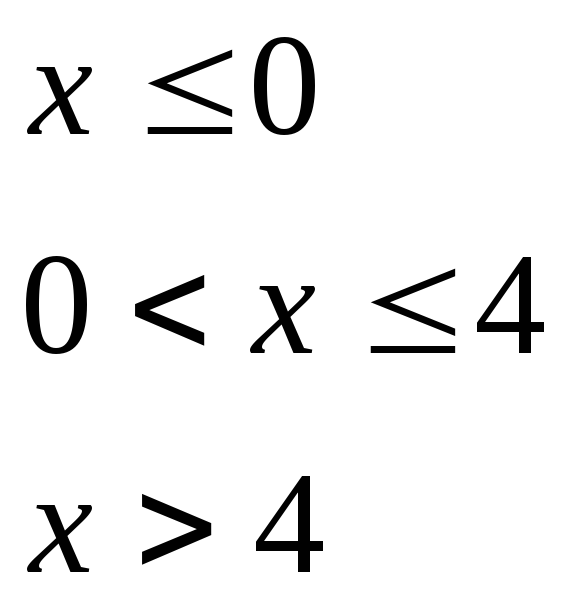
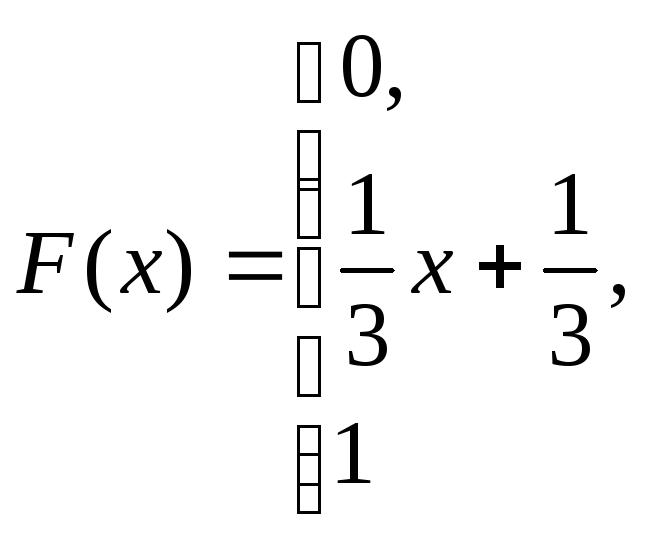 при
при