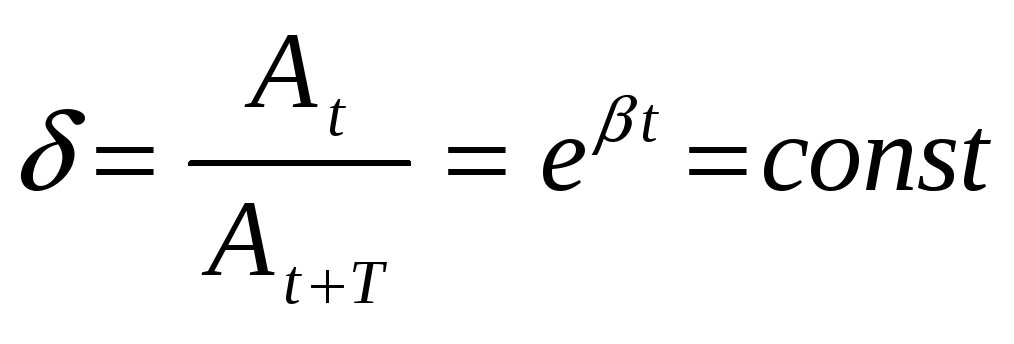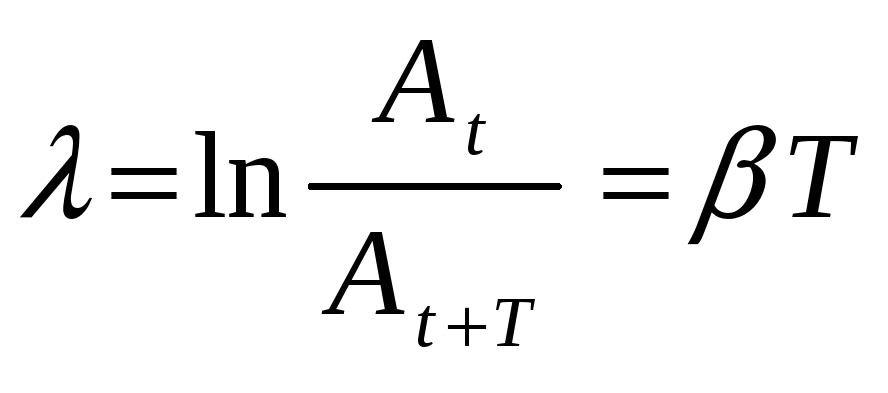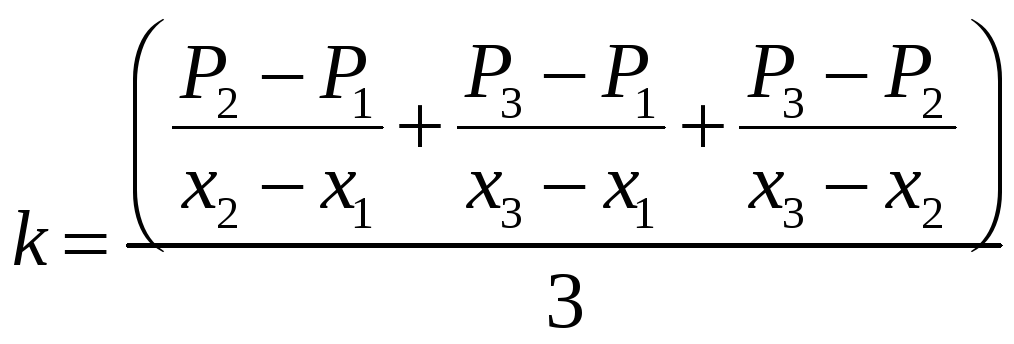Lab93
.docУДК 534. 014
Методическое указание к выполнению лабораторной работы «Собственные и затухающие колебания пружинного маятника».
Сост.: Федун В.И., Джеренова А.В. – Мариуполь, ПГТУ, 2007, 13 с.
Данное методическое пособие содержит изложение теоретических положений собственных и затухающих колебаний, описание лабораторного стенда и порядок выполнения лабораторной работы. Пособие рекомендуется для студентов очной и заочной форм обучения.
|
Рецензент: |
|
В.И. Жук, зав. кафедрой физики |
|
Составители: |
|
В.И. Федун, Джеренова А.В., ст. преподаватели кафедры физики
|
|
Ответственный за выпуск: зав. кафедрой физики Жук В.И., доц.
|
|
|
|
|
Утверждено на заседании кафедры физики протокол № 7 от “ 21 ” марта 2007 года
|
|
|
Рекомендовано методической комиссией сварочного факультета
Протокол № 5 от « 26 » марта 2007 г. |
||
Лабораторная работа № 93
«Собственные и затухающие колебания пружинного маятника»
Цель работы: опытным путем определить параметры собственных колебаний пружинного маятника, исследовать затухающие колебания физического маятника и рассчитать коэффициент сопротивления движению тела в жидкости.
Приборы и принадлежности: набор пружин и грузов, штатив, секундомер, сосуд с вязкой жидкостью.
1. Краткие теоретические сведения.
Колебательным движением называется движение, обладающее той или иной степенью повторяемости во времени. Движение называется периодическим, если значения величин, изменяющихся в процессе движения. Повторяются через равные промежутки времени.
Систему, совершающую колебания, независимо от ее природы называют осциллятором.
-
Свободные колебания. Для тела (точки), совершающей колебания, существует положение устойчивого равновесия. Вывести тело из этого состояния можно, приложив внешнюю силу. Тело, выведенное из состояния равновесия и представленное самому себе, совершает колебания около положения равновесия. Такие колебания называются собственными или свободными. Частота
 ,
с которой система совершает такие
колебания, называется собственной.
,
с которой система совершает такие
колебания, называется собственной.
Простейшим типом колебаний являются гармонические, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
|
|
где
![]() -
колеблющаяся величина (смещение,
скорость, ускорение, сила и т.п.),
-
колеблющаяся величина (смещение,
скорость, ускорение, сила и т.п.),
![]() -
время,
-
время,
![]() -
амплитуда колебания (амплитуда равна
максимальному абсолютному значению
отклонения колеблющейся величины от
положения равновесия),
-
амплитуда колебания (амплитуда равна
максимальному абсолютному значению
отклонения колеблющейся величины от
положения равновесия),
![]() - циклическая или круговая частота.
- циклическая или круговая частота.
Физический смысл
циклической частоты состоит в том, что
она численно равна числу колебаний,
совершаемых за
![]() секунд,
т.е.
секунд,
т.е.
|
|
|
где
![]() -
частота колебаний, т.е. число колебаний,
совершаемых за единицу времени,
-
частота колебаний, т.е. число колебаний,
совершаемых за единицу времени,
![]() -
период колебаний – время, за которое
совершается одно полное колебание.
-
период колебаний – время, за которое
совершается одно полное колебание.
Величина
![]() называется фазой колебания. Фаза
колебания – функция времени, которая
определяет значение колеблющейся
величины
называется фазой колебания. Фаза
колебания – функция времени, которая
определяет значение колеблющейся
величины
![]() в данный момент времени
в данный момент времени
![]() .
Она показывает, какую часть от амплитуды
.
Она показывает, какую часть от амплитуды
![]() составляет смещение в данный момент
времени:
составляет смещение в данный момент
времени:
![]() .
Величина
.
Величина
![]() называется начальной фазой колебания.
Она определяет значение величины
называется начальной фазой колебания.
Она определяет значение величины
![]() в начальный момент времени
в начальный момент времени
![]() .
.
|
|
|
Рис. 1. |
График гармонических колебаний изображен на рис. 1.
Дифференциальное уравнение гармонических колебаний с одной степенью свободы (см. рис. 2.а) имеет вид
|
|
где
![]() -
смещение колеблющейся системы.
-
смещение колеблющейся системы.
Если в уравнение (1.2) подставить одно из решений (1.1), то получим
|
|
|
|
а) |
|
откуда
Если система может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, то такая система обладает двумя степенями свободы (рис. 2 б). Если система совершает колебания около положения равновесия (после того как она каким-либо образом была выведена из положения устойчивого равновесия) без воздействия переменных внешних сил., то такие колебания называются собственными или свободными Частота, с которой система совершает такие колебания, называется собственной частотой системы. |
|
|
|
|
|
б) |
|
|
|
с) |
|
|
|
Рис. 2. |
||
-
Пружинный маятник. Примером гармонического осциллятора является пружинный маятник. Пружинный маятник – это груз массой т, закрепленный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой или квазиупругой силы
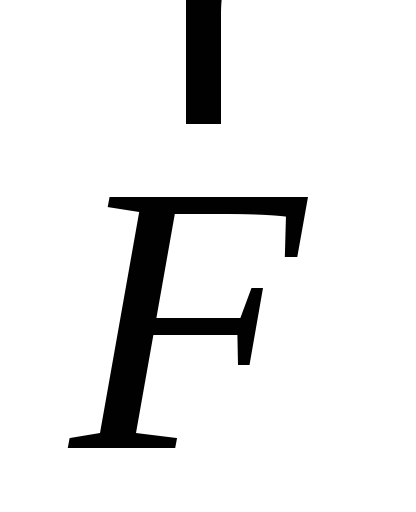 (силы, имеющие иную природу, чем упругие
силы, но также удовлетворяющие уравнению
(силы, имеющие иную природу, чем упругие
силы, но также удовлетворяющие уравнению
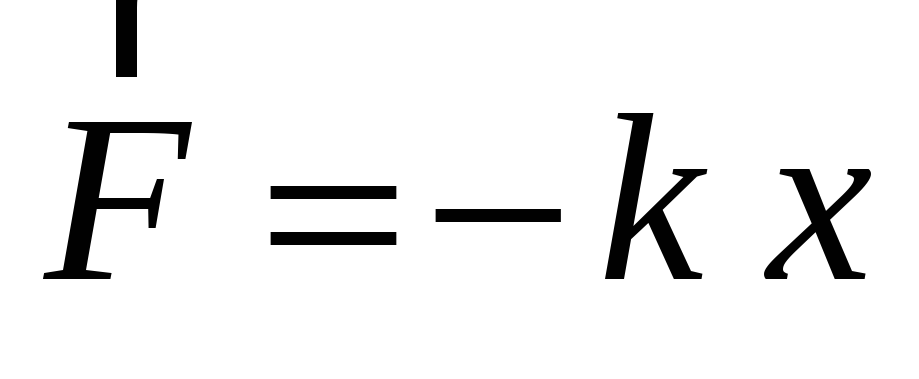 ,
называются квазиупругими). Эта сила
всегда направлена к положению равновесия,
а смещение
,
называются квазиупругими). Эта сила
всегда направлена к положению равновесия,
а смещение
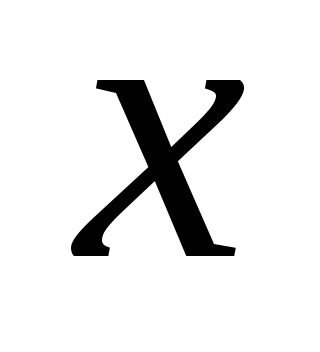 -
в противоположную сторону, поэтому
значения силы и смещения имеют
противоположные знаки. Такая сила
называется возвращающей силой. По
второму закону Ньютона для возвращающей
силы имеем
-
в противоположную сторону, поэтому
значения силы и смещения имеют
противоположные знаки. Такая сила
называется возвращающей силой. По
второму закону Ньютона для возвращающей
силы имеем
|
|
где
![]() -
масса груза,
-
масса груза,
![]() -
коэффициент упругости пружины,
-
коэффициент упругости пружины,
|
|
где
![]() -
циклическая частота,
-
циклическая частота,
![]() -
период собственных колебаний.
-
период собственных колебаний.
Из формулы (1.5) легко определить период собственных упругих колебаний груза на пружине. Так как
|
|
|
то
|
|
-
Затухающие колебания. Если колеблющаяся система находится в вязкой среде, то колебания через некоторое время прекратятся. Это явление представляет собой затухающее колебание.
Затухающими колебаниями называются колебания, энергия которых уменьшается с течением времени. В результате амплитуда колебаний уменьшается и колебания затухают.
Система тел,
механическая энергия которых постепенно
уменьшается за счет преобразования в
другие виды энергии, называется
диссипативной. Все реальные колебательные
системы являются диссипативными. Энергия
в диссипативной системе расходуется
на работу против сил трения. Затухающие
колебания совершаются при действии
двух сил: упругой силы
![]() и силы сопротивления
и силы сопротивления
![]() среды. Уравнение затухающего колебания
при небольших затуханиях имеет вид:
среды. Уравнение затухающего колебания
при небольших затуханиях имеет вид:
|
|
|
или
|
|
|
где
![]() -
масса колеблющегося тела,
-
масса колеблющегося тела,
![]() -ускорение
тела,
-ускорение
тела,
![]() -
величина возвращающей силы,
-
величина возвращающей силы,
![]() -сила
сопротивления среды,
-сила
сопротивления среды,
![]() - коэффициент сопротивления среды,
- коэффициент сопротивления среды,
![]() -
скорость движения тела в среде. Решение
уравнения (1.7) дает зависимость смещения
-
скорость движения тела в среде. Решение
уравнения (1.7) дает зависимость смещения
![]() от времени
от времени
![]() :
:
|
|
|
где
![]() - амплитуда затухающих колебаний,
- амплитуда затухающих колебаний,
![]() - основание натурального логарифма,
- основание натурального логарифма,
![]() - коэффициент затухания,
- коэффициент затухания,
![]() - циклическая частота затухающих
колебаний системы,
- циклическая частота затухающих
колебаний системы,
![]() - собственная циклическая частота
свободных колебаний системы (колебаний
системы вне вязкой среды).
- собственная циклическая частота
свободных колебаний системы (колебаний
системы вне вязкой среды).
|
|
График затухающих
колебаний при
Отношение двух
последующих амплитуд одного и того
же знака
|
|
|
|
||
и называется декрементом затухания. Натуральный логарифм от этого отношения
|
|
|
называется логарифмическим декрементом затухания.
В случае небольших
затуханий
![]() можно считать, что
можно считать, что
![]() .
Тогда
.
Тогда
|
|
-
Описание установки.
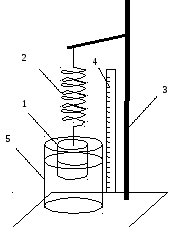
В данной работе рассматриваются два вида колебаний. Опыты проводят на лабораторном стенде (рис. 4), в состав которого входят: груз 1, пружина 2, штатив 3, измерительная линейка на подставке 4, сосуд с вязкой жидкостью 5.
|
|
|
|
Рис. 4 |
|
В первом упражнении
изучают колебания маятника в воздухе.
Поскольку в этом случае сила сопротивления
воздуха пренебрежимо мала по сравнению
с амплитудой возвращающей силы пружины,
колебания можно считать собственными
незатухающими. Такие колебания описываются
уравнениями (1.1). В этом упражнении
опытным путем определяют коэффициент
жесткости пружины
![]() ,
измеряя величину деформации пружины
,
измеряя величину деформации пружины
![]() вызванную
весом
вызванную
весом
![]() груза.
Согласно закону Гука величина силы
груза.
Согласно закону Гука величина силы
![]() упругости пружины прямо пропорциональна
деформации (удлинению) пружины:
упругости пружины прямо пропорциональна
деформации (удлинению) пружины:
|
|
(2.1) |
Если к пружине
подвешен неподвижный груз, то сила
![]() упругости равна по модулю весу
упругости равна по модулю весу
![]() тела (
тела (![]() =
=![]() ),
следовательно:
),
следовательно:
|
|
(2.2) |
Во втором упражнении предметом изучения являются затухающие колебания затопленного в жидкости 5 груза 1, подвешенного на пружине 2 (см. рис. 4). Эти колебания подчиняются уравнению (1.7).
3. Измерения и обработка результатов измерений.
3.1. Упражнение 1. Определение коэффициента жесткости пружин.
-
С помощью динамометра измерить веса входящих в комплект лабораторного стенда грузов (имеющих форму цилиндра, параллелепипеда и шара). Полученные результаты взвешиваний записать в колонку
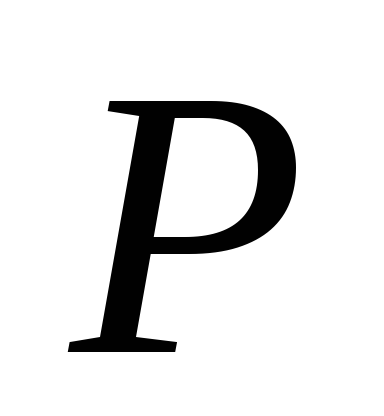 таблицы 1.
таблицы 1. -
К каждой из имеющихся на стенде пружин подвесить в следующем порядке тела:
|
|
- тело в форме параллелепипеда; |
|
|
- тела в форме параллелепипеда и цилиндра; |
|
|
- тело в форме шара. |
С помощью
измерительной линейки на подставке 4
(см. рис.4) измерить положения точки
подвеса тел к пружине. Результаты
измерений записать в колонку
![]() таблицы 1. Т.к. положение нижнего конца
ненагруженной пружины (при данной
методике измерений) является трудно
определимой величиной, то опытное
определение коэффициента жесткости
пружины
таблицы 1. Т.к. положение нижнего конца
ненагруженной пружины (при данной
методике измерений) является трудно
определимой величиной, то опытное
определение коэффициента жесткости
пружины
![]() сделаем следующим образом. Пусть
положение нижнего конца свободной
пружины есть
сделаем следующим образом. Пусть
положение нижнего конца свободной
пружины есть
![]() ,
а при подвешивании к пружине груза весом
,
а при подвешивании к пружине груза весом
![]() оно составит
оно составит
![]() .
Тогда формулу (2.2) запишем в виде
.
Тогда формулу (2.2) запишем в виде
|
|
(2.3) |
Так как при трех
измерениях для различных грузов и одной
пружины величины
![]() и
и
![]() являются неизменными, то из уравнений
(2.3) можно определить коэффициент
жесткости пружины, исключив неизвестную
величину
являются неизменными, то из уравнений
(2.3) можно определить коэффициент
жесткости пружины, исключив неизвестную
величину
![]() следующим образом:
следующим образом:
|
|
(2.4) |
Результаты
вычислений величины
![]() для каждой пружины занести в таблицу 1
в соответствующую колонку.
для каждой пружины занести в таблицу 1
в соответствующую колонку.
-
Определить зависимость периода собственных колебаний пружинных маятников от массы груза. Для этого измерить секундомером время
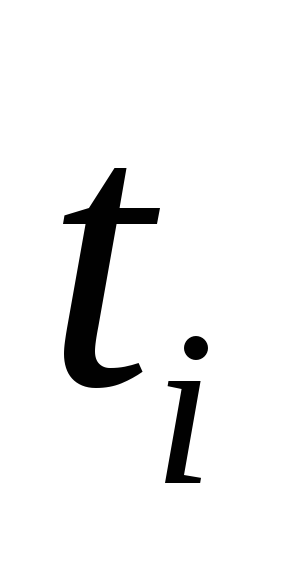 полных
полных
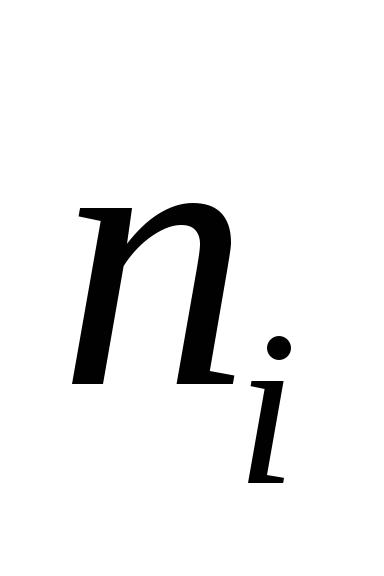 колебаний маятника, а период
колебаний маятника, а период
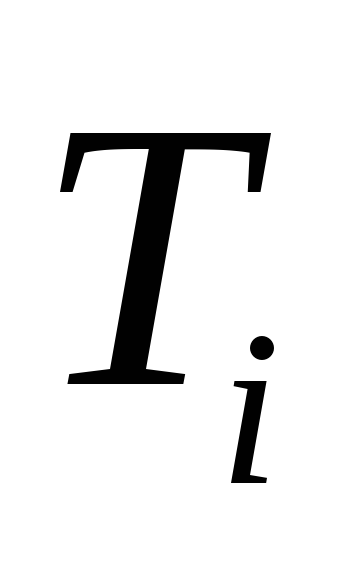 собственных колебаний определить по
формуле
собственных колебаний определить по
формуле
|
|
(2.5) |
для каждой из
пружин при различных грузах (таких же
как и в п. 3.1.2), имеющих массы
![]() .
Построить
график зависимости
.
Построить
график зависимости
![]() от
от
![]() (по
оси абсцисс откладывают массу
(по
оси абсцисс откладывают массу
![]() ).
).
-
Найти зависимость собственных колебаний пружинного маятника от коэффициента жесткости пружин
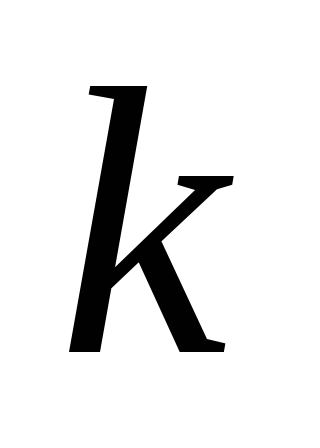 .
Для этого взять из таблицы 1 значения
периода
.
Для этого взять из таблицы 1 значения
периода
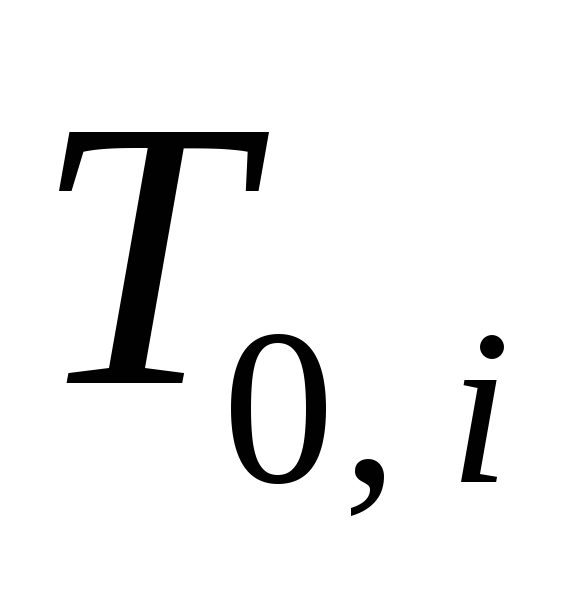 собственных колебаний маятников с
различными пружинами, нагруженных
одним и тем же грузом
собственных колебаний маятников с
различными пружинами, нагруженных
одним и тем же грузом
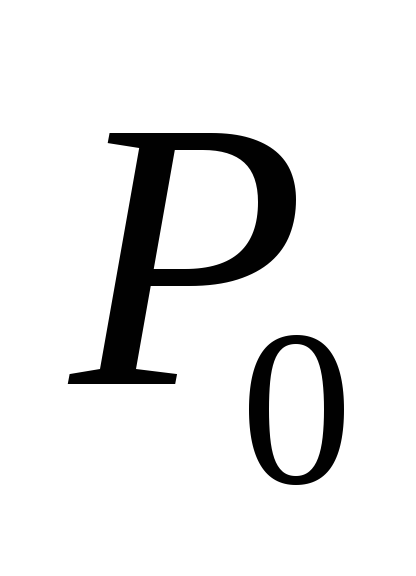 ,
а затем
построить
график
зависимости
,
а затем
построить
график
зависимости
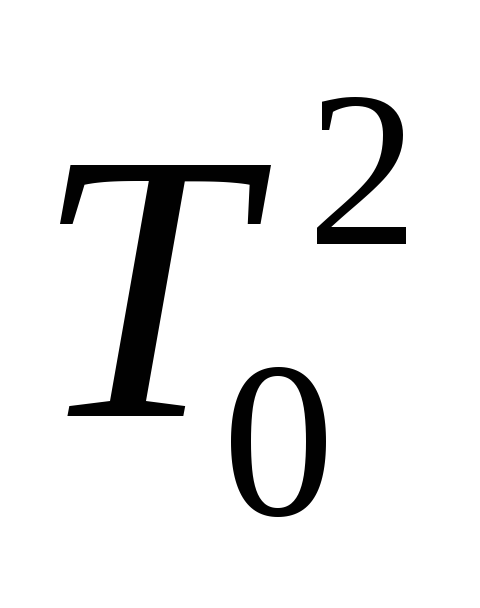 от величины, обратно пропорциональной
от величины, обратно пропорциональной
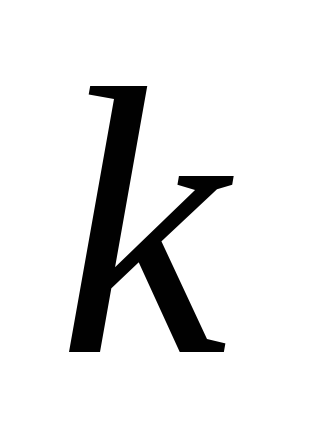 (по оси абсцисс откладывают значения
(по оси абсцисс откладывают значения
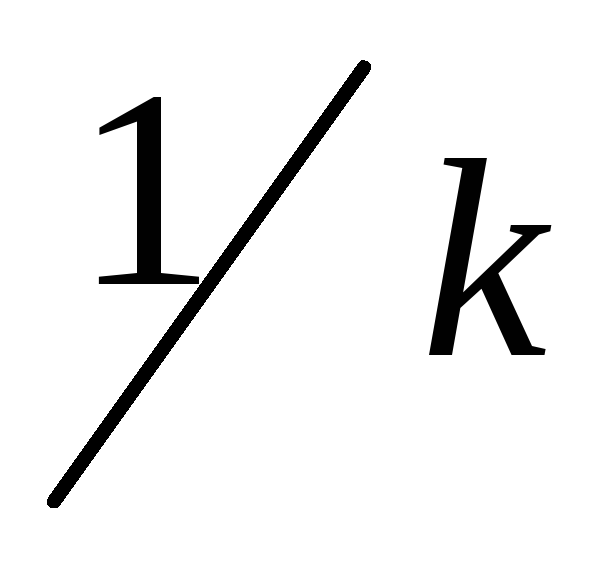 ).
). -
По формуле
|
|
(2.6) |
вычислить
теоретический коэффициент жесткости
пружин, используя полученные ранее (см.
п. 3.1.3) опытным путем значения
![]() .
Сравнить вычисленные значения
.
Сравнить вычисленные значения
![]() с результатами вычислений, проведенными
по формуле (2.4) для одних и тех же пружин.
Результаты анализа привести в выводах
к отчету.
с результатами вычислений, проведенными
по формуле (2.4) для одних и тех же пружин.
Результаты анализа привести в выводах
к отчету.
Таблица 1.
|
№№ опыта |
Н |
см |
Н/м |
с |
|
с |
|
|
|
|
I. |
Первая пружина |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
Средние значения |
|
|
|
|
|
||||
|
II. |
Вторая пружина |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
Средние значения |
|
|
|
|
|
||||
|
III. |
Третья пружина |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
Средние значения |
|
|
|
|
|
||||

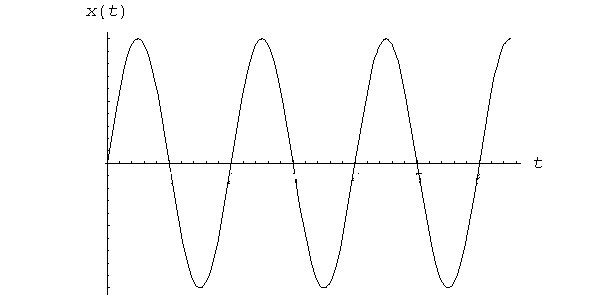
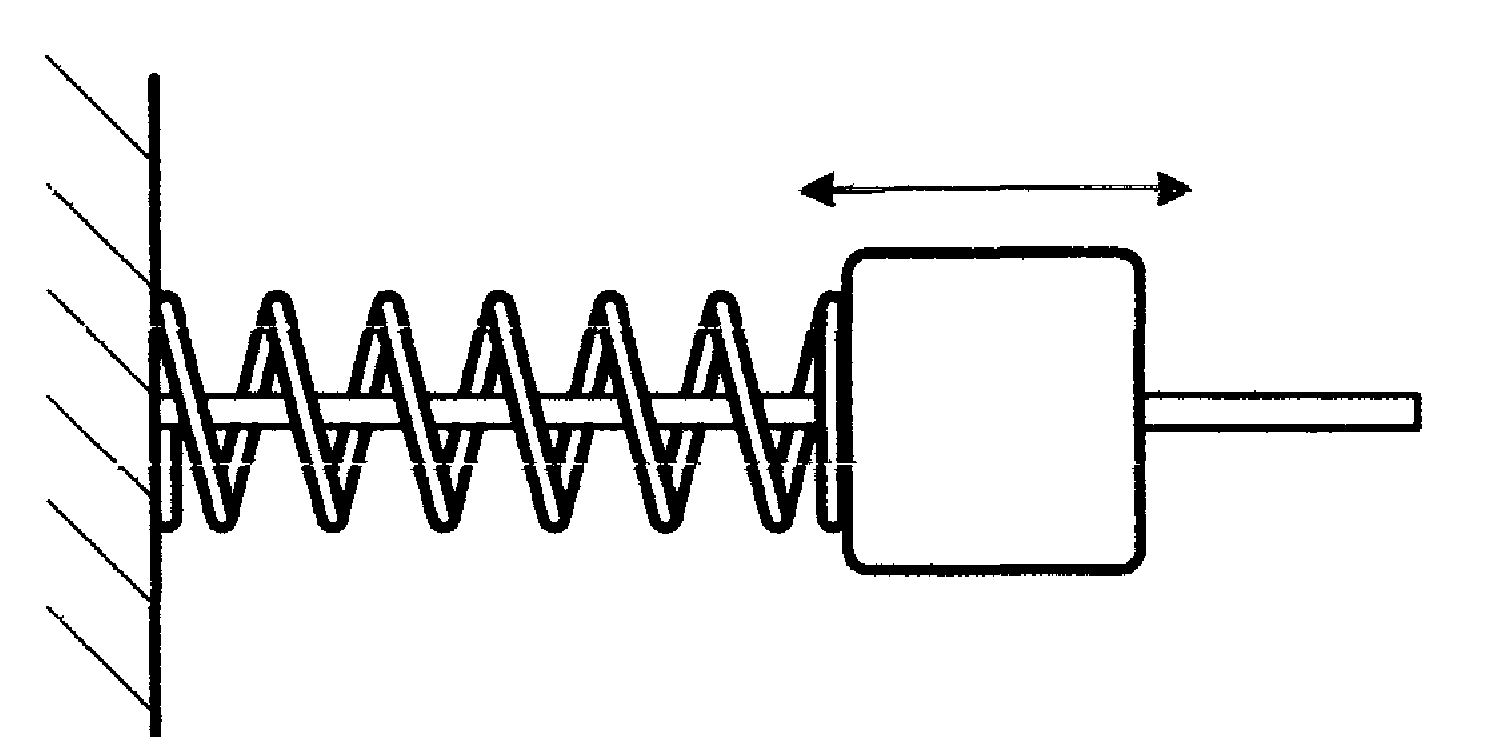
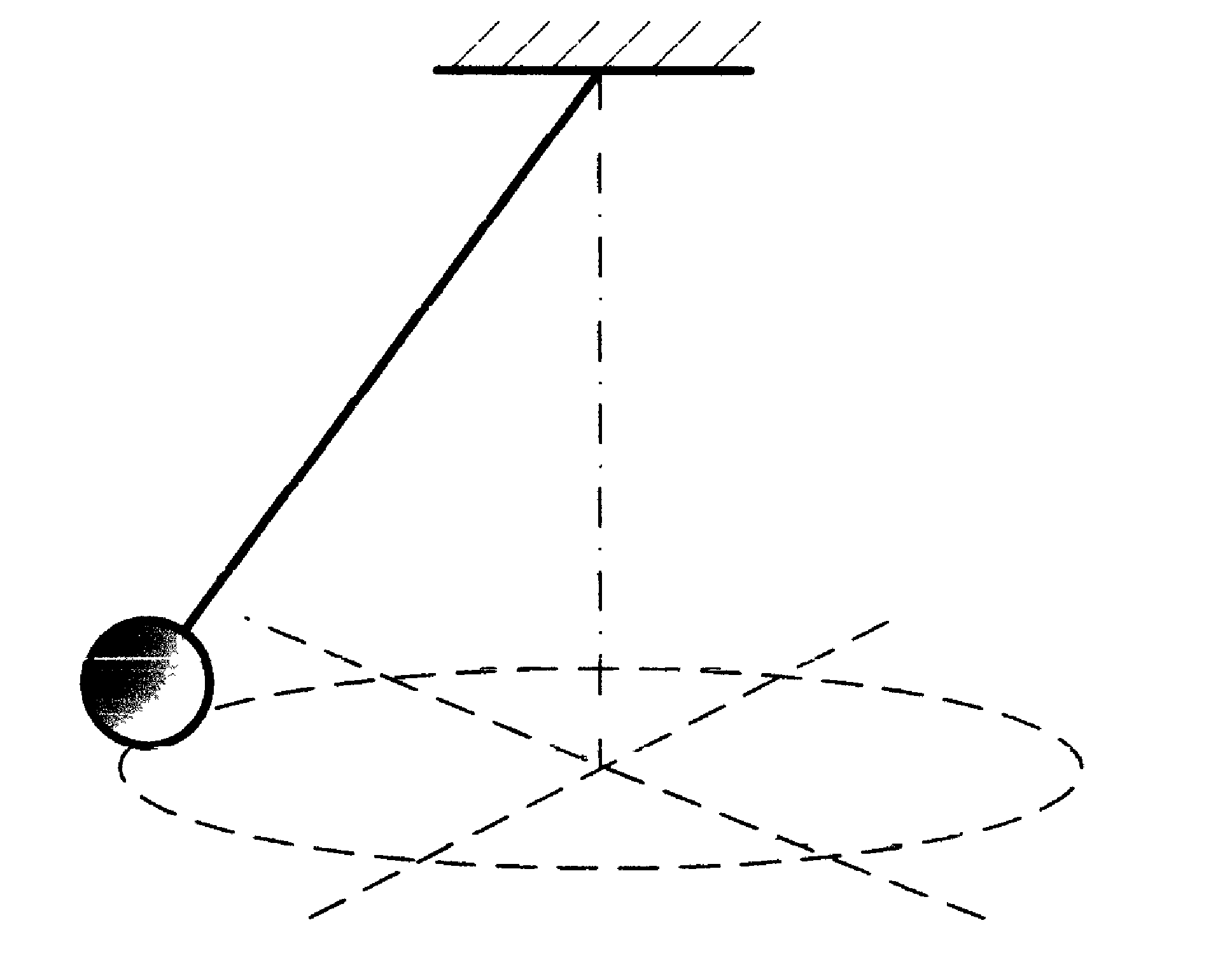
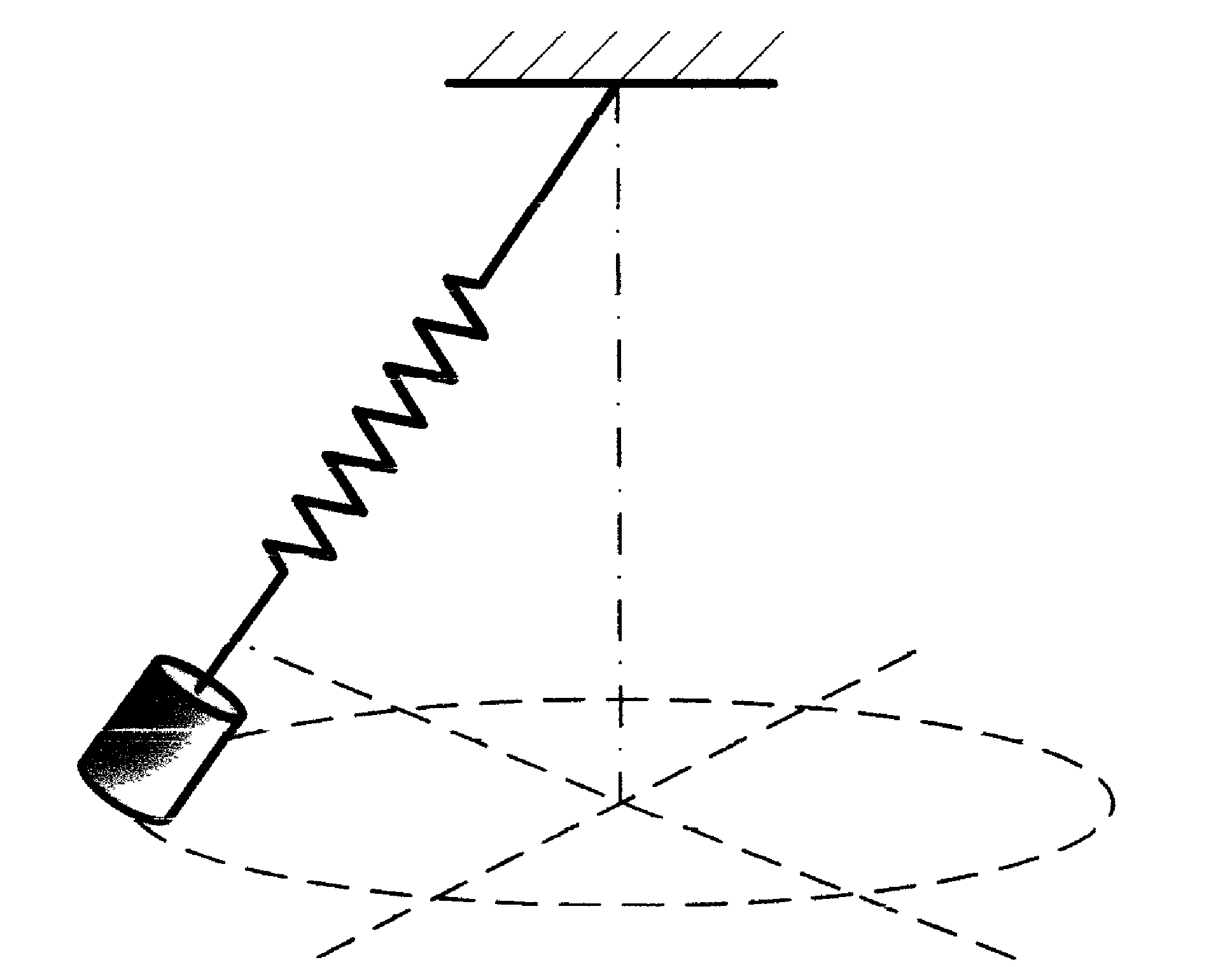
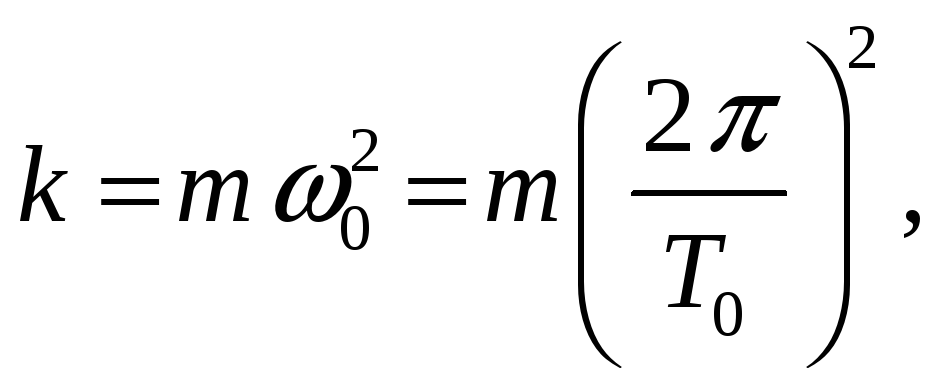
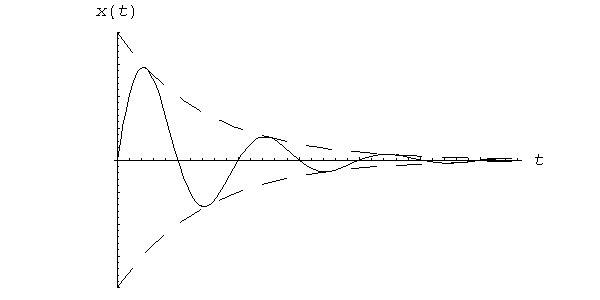 Рис.
3.
Рис.
3.