Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Полтавский национальный технический университет им. Ю. Кондратюка

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Цифровая обработка сигналов (сборник книг) / Белодедов М.В. Методы проектирования цифровых фильтров, 2004

.pdf

Скачиваний:

Добавлен:

05.03.2016

Размер:

902.07 Кб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Министерство образования Российской Федерации Волгоградский государственный университет

М.В.Белодедов

МЕТОДЫ ПРОЕКТИРОВАНИЯ ЦИФРОВЫХ ФИЛЬТРОВ

учебное пособие

Волгоград 2004

УДК 621.372.54

ББК 32.844 Б43

Рецензент д-р техн. наук, проф. каф. информационных систем и технологий

Самарского государственного аэрокосмического университета

С.А. Прохоров

Печатается в авторской редакции

Б43 Белодедов М.В. Методы проектирования цифровых фильтров: Учебное пособие. – Волгоград: Издательство Волгоградского государ- ственного университета, 2004. – 64 с.

ISBN 5-85534-929-2

В пособии дается систематическое изложение основных методов проекти- рования цифровых фильтров. Для обоснования применения излагаемых методов

рассматриваются свойства и методы анализа дискретных сигналов и дискретных систем. Теоретический материал подкреплен большим количеством практических примеров.

Пособие предназначено для студентов старших курсов технических специ- альностей, изучающих дисциплину «Цифровая обработка сигналов». Может ока- заться также полезным при изучении дисциплин «Теория цепей и сигналов», «Тео- ретические основы радиотехники».

ББК 32.844

ISBN 5-85534-929-2

ã М.В.Белодедов, 2004

ã Издательство Волгоградского государствнного университета, 2004

	Содержание
1.	Дискретные сигналы и их основные свойства.	4
2.	Цифровые фильтры.	12
3.	Цифровые фильтры с сосредоточенными параметрами.	18
4.	Структуры построения цифровых фильтров.	25
5.	Проектирование цифровых фильтров методом взвешивания.	30
6.	Проектирование цифровых фильтров методом частотной выборки	36
7.	Методы отображения дифференциалов.	41
8.	Метод инвариантного преобразования импульсной характеристики.	51
9.	Подбор нулей и полюсов передаточной характеристики.	55
10. Литература		60

1. Дискретные сигналы и их основные свойства.

Подавляющее большинство сигналов, обрабатываемых современными техническими системами, так или иначе имеет цифровое представление, ко- торое можно рассматривать с двух точек зрения. Во-первых, значение сигна- ла в данный конкретный момент времени, являясь по сути непрерывным, может быть воспринято любой обрабатывающей системой как одно из ко- нечного набора значений. Наиболее часто встречающимся случаем подобно-

го цифрового представления является преобразование непрерывного сигнала каким-либо АЦП. Такое цифровое представление непрерывного по сути зна- чения сигнала принято называть дискретизацией по уровню. Во-вторых, ин- формация о сигнале, зависящем, например, от времени (даже в том случае, если значения этого сигнала дискретизированы по уровню) не может быть

предоставлена обрабатывающей системе в виде значений сигнала в каждый момент непрерывно изменяющегося времени. Обрабатывающая система мо- жет оперировать лишь конечным набором значений сигнала и такое пред- ставление непрерывно изменяющегося сигнала принято называть дискрети- зацией по времени. В большинстве практических применений уровни дискре-

тизации значений сигнала выбираются равно отстоящими друг от друга и расстояние между ними называется интервалом дискретизации по уровню.

Аналогично моменты дискретизации сигнала по времени выбираются обыч-

но равно отстоящими друг от друга и расстояние между ними называется

интервалом дискретизации по времени. Как правило, замена непрерывных

значений сигнала дискретными уровнями может быть аналитически учтена добавлением в обрабатываемый сигнал равномерно распределенного в неко- тором интервале шума и не приводит к каким-либо неожиданным следстви- ям. Замена же непрерывно изменяющегося сигнала дискретным набором зна- чений, напротив, приводит к ряду интересных эффектов, которые, собствен- но, и составляют предмет изучения теории цифровой обработки сигналов

(digital signal processing).

Итак, далее мы будем рассматривать системы, обрабатывающие дис- кретный набор дискретных значений сигнала. Если обратиться к упомянуто- му АЦП, интервал дискретизации по уровню определяется разрядностью АЦП и уменьшается с увеличением разрядности, интервал же дискретизации

по времени определяется частотой дискретизации АЦП и уменьшается с ее ростом. В приведенном примере изменение сигнала происходит с изменени- ем времени и дискретный набор значений сигнала соответствует разным мо- ментам времени. Большинство дискретных сигналов имеет именно такую природу. Следует учитывать, однако, что практический интерес могут иметь также сигналы, зависящие не от времени, а от какой-либо другой непрерыв- ной величины, например, от пространственной координаты. Будем, тем не менее, в основном рассматривать сигналы, зависящие именно от времени и обозначать интервал дискретизации по времени символом . Эффекты, свя- занные с дискретизацией по уровню, обычно учитывать не будем, предпола-

гая, что интервал дискретизации по уровню достаточно мал, чтобы считать эти эффекты пренебрежимо малыми.

Итак, определим дискретный сигнал как не более чем счетный (на практике, разумеется, конечный, но для удобства аналитического рассмотре- ния имеет смысл учесть вариант бесконечного числа отсчетов) набор вели- чин, заданных в моменты времени n и принимающих непрерывный (на практике, разумеется, дискретный) ряд значений. Для значения дискретного сигнала в n-ный момент времени введем обозначение xn (эти значения будем

далее называть отсчетами сигнала), а сам сигнал обозначим как x. Назовем также конечным сигналом дискретный сигнал, имеющий конечное число от- личных от нуля значений и ограниченным сигналом дискретный сигнал, сумма абсолютных значений отсчетов которого конечна, или, иными слова-

∞

ми, тот сигнал x, для которого сходящимся является ряд å xn . Примером

n =−∞

дискретного сигнала может служить сигнал x, значения отсчетов которого определяются выражением xn = Asin(ωn ). Такой сигнал имеет смысл назы-

вать гармоническим сигналом с амплитудой A и частотой ω. Частота ω ино- гда называется циклической частотой и имеет физический смысл «количест- во радиан в единицу времени» в отличие от обыкновенной частоты f = ω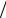(2π), имеющей смысл «количество периодов в единицу времени».

При рассмотрении непрерывных сигналов (теория цепей и сигналов,

см., например, [С.И.Баскаков. Радиотехнические цепи и сигналы. – М.: Высшая школа, 1983, с.51.]), основополагающее значение имеет понятие спектра сигнала, оп- ределяемого выражением:

∞

X (ω) = ò x(t)e− jωt dt .

−∞

Понятие спектра дискретного сигнала легко ввести, если поставить ему в соответствие непрерывный сигнал, представляющий собой набор δ- функций, сосредоточенных в моменты времени t = n , и имеющих амплиту- ды xn :

xнепр. (t) =		∞
xнепр. (t) =		åxnδ(t − n ).		(1.1)
	n =−∞
Спектром дискретного сигнала можно теперь назвать спектр соответст-
вующего ему непрерывного сигнала:
∞		∞	∞
X (ω) = ò xнепр. (t)e− jωtdt =		ò	åxnδ(t − n	)e− jωtdt =
−∞		−∞ n =−∞
∞	∞		∞
= å xn òδ(t − n		)e− jωtdt = åxne− jωn .
n =−∞	−∞		n= −∞

Множитель в выражении (1.1) был введен единственно с той целью, чтобы определенные интегралы от непрерывного сигнала xнепр. (t) не зависе-

ли от интервала дискретизации по времени. При неизменном интервале дис- кретизации этот множитель можно опустить. Будем, таким образом, называть

спектром дискретного сигнала x величину:

∞
X (w) = åxne− jωn .	(1.2)

n =−∞

Если отсчеты сигнала являются чисто действительными (а в большин- стве случаев это действительно так), спектр является симметричной функци- ей:

∞	∞		∞		æ	∞
X (- w) = åxne jωn =	åxn (e− jωn	) =	å(xne− jωn	)	= çç	åxne− jωn
n =−∞	n =−∞		n =−∞		èn = −∞

ö	= X (w)
÷	= X (w)
÷
ø

где символом обозначена операция комплексного сопряжения.

Введенный таким образом спектр дискретного сигнала обладает таким неожиданным свойством, как периодичность. Действительно, вычислим зна- чение спектра на частоте ω + 2π :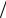

∞		∞		∞
X (w + 2p D) = åxne− j(ω+2	π	)n = åxne− jωn e− j2	πn =	åxne− jωn = X (w).
n =−∞		n =−∞		n =−∞

Как известно, спектры непрерывных сигналов не обладают периодич- ностью. Выявленная периодичность спектра присуща именно дискретным сигналам и обусловлена, вообще говоря, тем фактом, что само понятие час- тота определена для дискретного сигнала неоднозначно. Так, например, гар-

монический сигнал с частотой ω + 2π	совпадает с гармоническим сигна-
лом с частотой ω:
Asin((ω + 2π )n ) = Asin(ωn + 2πn	)= Asin(ωn + 2πn)= Asin(ωn ).

Если непрерывный сигнал имеет верхнюю граничную частоту ωВ , то есть сосредоточен в полосе частот [− ωВ ... +ωВ ], то при его дискретизации с

интервалом дискретизации периодические повторы его спектра не будут накладываться друг на друга при выполнении условия ≤ πωВ = 1(2 fВ ).

Сформулированное условие называется условием Котельникова (хотя за ру- бежом его чаще связывают с именем Найквиста) и обычно определяет часто- ту дискретизации непрерывных сигналов.

Вычислим спектр часто встречающегося прямоугольного сигнала

ì1

при

- N £ n £ N

= í

при

> N

î0

X (w) = åe− jωn =

åe− jωn + åe− jωn -1 = åe jωn + åe− jωn -1 =

n =− N

n =0

n=0

n =0

1- e jω(N +1)

1- e− jω(N +1)

-1 =

1- e jω

1- e− jω

1− e jω(N +1)

− e− jω + e jωN

+1− e− jω(N +1)

− e jω

+ e− jωN

−1 =

(1− e jω

)(1− e− jω )

2 − 2cos(ω(N +1)

)− 2cos(ω )+ 2cos(ωN )

−1 =

2 − 2cos(ω )

ω(2N +1)

− cos(ω(N +1) )+ cos(ωN )

sin

= 2

1− cos(ω )

2sin

sin

Итак, спектр прямоугольного сигнала имеет вид:

		X (ω) =	sin(ω(N +1 2)		)	.			(1.3)
		X (ω) =				.
			sin(ω	2)
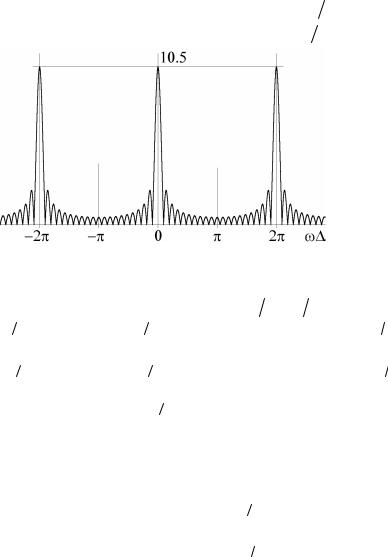
							Форма модуля спектра (1.3)
					при		N = 10 показана		на рис.1.
					Значение спектра			на	частоте
					ω = 0 легко получить,				вычисляя
					соответствующий предел функ-
					ции (3). Нетрудно заметить, что
					вычисленный спектр				обладает
					как симметрией, так и перио-
					дичностью.
	Рис.1. Форма модуля спектра (3) при N = 10 .						Выражение (2) можно обра-
	Рис.1. Форма модуля спектра (3) при N = 10 .				тить, то есть выразить отсчеты
					тить, то есть выразить отсчеты
xn	через спектр X (ω). Для этого домножим обе части равенства (2) на e jωn
и проинтегрируем по периоду [− π ...π				]:
π	π	∞		∞			π	2π xn′ .
ò X (ω)e jωn′ dω = ò		åxne− jωn e jωn′ dω = å xn					òe jω(n′−n ) dω =	2π xn′ .
− π	−π	n= −∞		n= −∞			−π
	При выводе последнего выражения использован тот общеизвестный
		π		2π ,
факт, что интеграл		òe jω(n′−n) dω равен		2π ,	если n = n′, и нулю в противном

− π

случае. Окончательно отсчеты дискретного сигнала выражаются через его спектр следующим образом:

		π
xn =		ò X (ω)e jωn dω.	(1.4)
xn =	2π	ò X (ω)e jωn dω.	(1.4)
		−π

Приблизительно столь же важное значение, как спектр (или преобразо- вание Фурье) для непрерывных сигналов, для дискретных сигналов имеет так называемое z-преобразование. Оно определяется следующим образом:

∞
Z[x]= X (z)= åxn z−n ,	(1.5)

n=−∞

то есть дискретному сигналу x ставится в соответствие комплексная функция X (z) комплексного аргумента z, представляющая собой степенной ряд

[Г.Е.Шилов. Математический анализ (функции одного переменного). – М.: Наука, 1969,

с.238], коэффициентами которого являются отсчеты сигнала x. Z- преобразование сигнала x может быть определено не на всей комплексной z- плоскости, та область плоскости, где оно определено, то есть ряд (1.5) схо- дится, называется областью сходимости. Рассмотрим несколько примеров.

ì1 при n = 0;

Пример 1. Единичный сигнал e: en = í

î0 при n ¹ 0.

∞

Z[e]= E(z)= åen z−n = z0 =1.

n=−∞

Z-преобразование единичного сигнала тождественно равно единице, область схо- димости – вся z-плоскость.

Пример 2. Экспоненциально убывающий (или нарастающий) сигнал:

x : x		ì0	при n < 0;
	n	= í	при n ³ 0.
		îan

Его z-преобразование вычислим как сумму геометрической прогрессии:

∞	∞	∞	1
Z[x]= X (z)= åxn z−n = åan z−n = å(az−1 )n =			1	.
Z[x]= X (z)= åxn z−n = åan z−n = å(az−1 )n =			1	.
n=−∞	n=0	n=0	1- az−

Приведенные вычисления справедливы только в том случае, если знаменатель про- грессии az−1 по абсолютному значению не превосходит единицы, в противном случае ряд (1.5) расходится, то есть функция X (z) определена только для z, удовлетворяющих усло-

вию z > a . Таким образом, областью сходимости z-преобразования сигнала x является

часть комплексной z-плоскости, являющаяся внешней по отношению к окружности с цен- тром в точке z = 0 и радиусом a .

Пример 3. Гармонический сигнал

при n < 0;

x : xn

ì0

= í

при n ³ 0.

îAsin(wnD)

Для вычисления z-преобразования представим синус в виде суммы экспонент:

sin(wnD)= (e jωn

- e− jωn

) 2 j :

∞

A æ

∞

Z[x]= X (z) = åxn z−n =

åe jωn z−n -

åe− jωn

z−n ÷

n=−∞

2 j è n=0

n=0

A æ

∞

A æ

(e jω z−1 )

- å(e− jω z−1 )

- e

jω

−1

- e

− jω

−1

2 j è n=0

n=0

2 j è1

e jω

z−1 - e− jω z−1

= Az−1

sin(wD)

2 j

(1 - e jω

z−1 )(1 - e− jω

z−1 )

1 - 2z−1 cos(wD)+ z−2

Область сходимости вычисленного z-преобразования –

> 1.

Пример 4. Рассмотрим абстрактный гармонический сигнал

x: xn = e jω0n ,

который назван абстрактным, во-первых, потому, что, в отличие от предыдущих приме- ров, он не начинается в момент времени 0, а длится «всегда», от n = −∞ до n = ∞ , и, во- вторых, принимает комплексные значения, что на практике реализовано быть не может. Такие сигналы, тем не менее, играют большую роль в математическом анализе дискрет- ных систем, поскольку все реальные сигналы можно представить в виде линейной комби- нации рассматриваемых сигналов. Так, например,

sin(ω n	) = (e jω0n	− e− jω0n	) 2 j ,
0
cos(ω n	) = (e jω0n	+ e− jω0n	) 2 , и т.д.
0

Итак, найдем z-преобразование абстрактного гармонического сигнала:

∞

Z[x]= åe jω0n z

−n = åe jω0n z−n +

åe jω0n z−n −1 =

n=−∞

n=0

−1 )n −1 =

∞

= åe− jω0n zn + åe jω0n z−n −1 = å(e− jω0 z)n +

å(e jω0 z

n=0

−1.

1− e− jω0 z

1− e jω0 z−1

Анализируя последнее выражение, нетрудно убедиться, что оно равно нулю прак-

тически везде:

1− e jω0 z−1 +1− e− jω0 z

−1=

−1

1− e− jω0 z

1− e jω0 z−1

(1− e− jω0 z)(1− e jω0 z−1 )

2 − e jω0

z−1

− e− jω0 z

−1 = 0,

− e jω0

z−1

− e− jω0 z

за исключением точки z = e jω0

, где оно обращается в бесконечность. Этот факт дает ос-

нование объявить искомое z-преобразование δ-функцией:

Z[x: xn = e jω0n

] = δ(z − e jω0 ).

(1.6)

Вообще говоря, это не совсем правильно, поскольку полученную δ-функцию мож- но без каких-либо последствий умножить на любую константу. Поиск точного значения этой константы представляет собой достаточно сложную математическую задачу, поэтому в дальнейшем будем использовать выражение (1.6) либо в представленном виде, либо с

неопределенной константой: Z[x: xn = e jω0n ] = C δ(z − e jω0 ).

Рассмотрим основные свойства z-преобразования.

1) Как это следует непосредственно из определения и уже было ис- пользовано в примере 3, z-преобразование линейно, то есть

Z[ax + by]= Z[ax]+ Z[by]= aZ[x]+ bZ[y] .

2) Z-преобразование задержанного сигнала. Пусть сигнал y представля- ет собой задержанный на один отсчет сигнал x, то есть yn = xn −1 . Тогда

∞	∞	∞
Z[y]= Y (z) = å yn z−n = åxn −1z−1z−(n −1) =z−1		åxn z−n =z−1X (z) = z−1Z[x]	(1.7
n =−∞	n =−∞	n =−∞	)
	,

то есть z-преобразование задержанного на один отсчет сигнала получается из z-преобразования исходного сигнала путем умножения его на z−1 . Легко по-

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в папке Цифровая обработка сигналов (сборник книг)

#
05.03.2016902.07 Кб92Белодедов М.В. Методы проектирования цифровых фильтров, 2004.pdf
#
05.03.2016863.2 Кб83Граничин О.Н. Введения в методы стохастической оптимизации и оценивания, 2003.pdf
#
05.03.2016958.12 Кб112Дронов С.В. Многомерный статистическийц анализ, 2003.pdf
#
05.03.2016109.31 Кб73Лазарев С. Быстрое Преобразование Ффурье,1999.pdf
#
05.03.20162.18 Кб56Цифровая обработка сигналов (сборник книг).txt