
Цифровая обработка сигналов (сборник книг) / Белодедов М.В. Методы проектирования цифровых фильтров, 2004
.pdf
Контрольные вопросы и задачи.
1.Конечную или бесконечную характеристику имеют фильтры, рас- считанные методом частотной выборки?
2.Может ли в результате применения метода частотной выборки полу- читься рекурсивный цифровой фильтр?
3.Можно ли схему рис.13 представить в виде первой или второй пря- мой формы?
4.Какими преимуществами по сравнению с методом взвешивания об- ладает метод частотной выборки?
5.Как обеспечить устойчивость цифрового фильтра при применении метода частотной выборки?
6.Предложите частотную выборку из 10 точек для реализации транс- версального цифрового фильтра с частотной характеристикой:
|
|
|
|
H (w)= íì1 при ω |
< π 10; |
|
|
|
|
|||||
|
|
|
|
|
|
î0 при wD > p 10. |
|
|
|
|||||
|
7. Пригодна ли для решения задачи 6 частотная выборка, приведенная в |
|||||||||||||
таблице? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
0 |
π 25 |
π 20 |
|
π 15 |
|
π 10 |
|
π 5 |
|
π 2 |
π |
3π 2 |
4π 5 |
H (ω) |
1 |
1 |
1 |
|
1 |
|
1 |
|
0 |
|
0 |
0 |
0 |
0 |
8.Можно ли, используя метод частотной выборки, проектировать циф- ровые фильтры с линейной фазово-частотной характеристикой?
9.К чему должно приводить увеличение точек частотной выборки?
10.Как соотносятся исходная частотная характеристика и частотная характеристика цифрового фильтра, построенного методом частотной вы- борки?
40
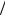
7. Методы отображения дифференциалов.
Большое количество методов проектирования цифровых фильтров опирается на известные из теории цепей и сигналов (или теоретические ос-
новы радиотехники, [С.И.Баскаков. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000, 462с.]) методы проектирования аналоговых (непрерывных) фильт- ров. Напомним без вывода некоторые основные положения теории непре- рывных цепей (для сравнения будем напоминать соответствующие свойства цифровых систем):
Для непрерывных сигналов существует |
Для дискретных сигналов существует z- |
|||||||
линейное преобразование Лапласа, ставя- |
преобразование, ставящее сигналу в соот- |
|||||||
щее сигналу в соответствие некоторую ве- |
ветствие некоторую вещественную функ- |
|||||||
щественную функцию, определенную на |
цию, определенную на комплексной плос- |
|||||||
комплексной плоскости: |
|
|
|
кости: |
|
∞ |
|
|
X (s) |
∞ |
|
|
|
|
|
|
|
= ò x(t)e−st dt . |
|
|
|
|
X (z) = åxn z−n . |
|||
|
−∞ |
|
|
|
|
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
Если непрерывный |
сигнал |
x(t) имеет |
Если дискретный сигнал xn имеет z- |
|||||
преобразование Лапласа |
X (s), |
то его про- |
преобразование |
X (z), то его задержанный |
||||
изводная dx(t) dt имеет преобразование |
сигнал |
xn−1 |
имеет |
z-преобразование |
||||
Лапласа sX (s). |
|
|
|
|
z−1 X (z). |
|
|
|
Спектр непрерывного сигнала |
|
Спектр дискретного сигнала |
||||||
X (ω) |
∞ |
|
|
|
|
|
∞ |
|
= ò x(t)e− jωt dt |
|
|
|
X (ω) = åxn e− jωn |
||||
|
−∞ |
|
|
|
|
|
n=−∞ |
|
|
|
|
|
представляет собой значения его z- |
||||
представляет собой значения его преобра- |
||||||||
зования Лапласа, |
взятые на мнимой |
оси |
преобразования, взятые на единичной ок- |
|||||
s = jω . |
|
|
|
|
ружности z = e jω . |
|
||
Линейные инвариантные |
аналоговые |
Линейные |
инвариантные дискретные |
|||||
цепи полностью характеризуются импульс- |
цепи полностью характеризуются импульс- |
|||||||
ной характеристикой h(t), причем входной |
ной характеристикой hn , |
причем входной |
||||||
(x) и выходной (y) сигналы цепи связаны |
(x) и выходной (y) сигналы цепи связаны |
|||||||
соотношением: |
|
|
|
|
соотношением: |
|
|
|
y(t) = x(t) h(t). |
|
|
|
|
yn = xn hn . |
|||
Преобразование Лапласа |
импульсной |
Z-преобразование импульсной характе- |
||||||
характеристики аналоговой цепи называет- |
ристики дискретной цепи называется пере- |
|||||||
ся передаточной |
характеристикой |
цепи |
даточной характеристикой цепи H(z), z- |
|||||
H(s), преобразования Лапласа входного и |
преобразования входного и выходного сиг- |
|||||||
выходного сигналов связаны друг с другом |
налов связаны друг с другом передаточной |
|||||||
передаточной характеристикой: |
|
|
характеристикой: |
|
||||
Y (s) = X (s)H(s). |
|
|
|
Y (z) = X (z)H(z). |
||||
Так же, как в случае с дискретными системами, в непрерывных систе- мах принято выделять цепи с сосредоточенными параметрами, которые стро- ятся из элементарных цепей, входной и выходной сигналы которых связаны линейными дифференциальными соотношениями. Подавляющее большинст- во аналоговых цепей, встречающихся на практике, являются цепями с сосре- доточенными параметрами. Приведем основные свойства цепей с сосредото- ченными параметрами.
41

Передаточная характеристика линейной |
Передаточная характеристика линейной |
|||||||||
аналоговой цепи с сосредоточенными пара- |
дискретной цепи с сосредоточенными па- |
|||||||||
метрами имеет вид отношения полиномов |
раметрами имеет вид отношения полиномов |
|||||||||
от аргумента s: |
P1 |
(s) |
|
от аргумента z−1 : |
||||||
H(s) = |
H(z) = |
P (z−1 ) |
||||||||
P2 |
(s) . |
1 |
. |
|
|
|
|
|||
P (z−1 ) |
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
Аналоговая цепь |
с |
сосредоточенными |
Дискретная цепь с сосредоточенными |
|||||||
параметрами является устойчивой тогда и |
параметрами является устойчивой тогда и |
|||||||||
только тогда, если ее передаточная характе- |
только тогда, если ее передаточная характе- |
|||||||||
ристика не имеет полюсов в правой части s- |
ристика не имеет полюсов за пределами |
|||||||||
плоскости: Re(s) > 0. |
|
|
|
единичной окружности z-плоскости: |
|
z |
|
> 1. |
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Теория аналоговых цепей обладает большим количеством рецептов по- строения фильтров с заданными свойствами (фильтры Бесселя, Баттерворта, Чебышева, фильтры низких и высоких частот, полосовые и заградительные фильтры, [У.Титце, К.Шенк. Полупроводниковая схемотехника: Справочное пособие. –
М.: Мир, 1982, с.185]). Всеми этими рецептами можно было бы воспользовать- ся, если бы удалось найти подходящее преобразование из s-плоскости в z- плоскость. Исходя из указанных свойств аналоговых и дискретных цепей, это преобразование должно обладать следующими свойствами.
1)Мнимая ось s-плоскости должна отображаться в единичную окруж- ность z-плоскости.
2)Левая полуплоскость s-плоскости Re(s)< 0 должна отображаться во
внутреннюю часть единичного круга z-плоскости z < 1.
3) Преобразование должно быть дробно-рациональным, поскольку именно такое преобразование будет отображать отношение полиномов от ар-
гумента s в отношение полиномов от аргумента z−1 , что позволит реализовы- вать цифровые фильтры с сосредоточенными параметрами.
В качестве искомого преобразования можно предложить замену произ- водной по времени конечной разностью:
dxdt → xn +1 − xn .
Если сделать преобразование Лапласа левой части этого выражения и z-преобразование правой части, то можно получить:
sX (s)→ z −1 X (z),
откуда и следует явный вид требуемого преобразования: |
|
||
s → |
z −1 |
, |
(7.1) |
|
|||
откуда следует обратное преобразование: |
|
||
z ← s +1. |
(7.1а) |
||
Описанный метод носит название метод прямой разности. Из соотно- шения (7.1а) следует, что левая полуплоскость s-плоскости переходит в ле- вую полуплоскость Re(z)< 1 z-плоскости, а мнимая ось s-плоскости – в пря-
42

мую Re(z)= 1 z-плоскости, то |
есть |
не выполняются сразу два из |
|
сформулированных требований. |
|
Полюсы передаточной характери- |
|
|
|
||
|
стики аналогового фильтра, лежащие в |
||
|
левой полуплоскости, могут отобра- |
||
|
зиться в полюсы передаточной харак- |
||
|
теристики цифрового фильтра, лежа- |
||
|
щие вне единичной окружности, как |
||
|
это изображено на рис.14 (символы ×), |
||
|
то есть при использовании метода пря- |
||
|
мой разности устойчивый аналоговый |
||
|
фильтр может отобразиться в неустой- |
||
|
чивый цифровой. |
|
|
|
|
Как видно из рис.14, условия 1) и |
|
Рис.14. Преобразование s → z |
2) |
выполняются вблизи |
точки z = 1 |
комплексной z-плоскости, |
то есть при |
||
в методе прямой разности. |
устремлении к нулю интервала дискре- |
||
|
|||
тизации по времени метод прямой разности должен давать удовлетворитель- ные результаты.
От некоторых недостатков метода прямой разности свободен метод об- ратной разности, в котором производная по времени апроксимируется раз- ностным выражением:
dx ® xn − xn −1 , dt D
что приводит к явному виду прямого и обратного преобразований:
s ® |
1- z−1 |
, |
(7.2) |
|||
|
|
D |
||||
|
|
|
|
|
||
z ¬ |
|
|
1 |
. |
(7.2а) |
|
1 |
- sD |
|||||
|
|
|
||||
Как видно из рис.15, образом мни- мой оси s-плоскости на z-плоскости
является окружность с центром в точке z = 1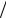 2 и радиусом 1/2. В самом деле,
2 и радиусом 1/2. В самом деле,
действительная часть точки образа рав- на:
æ |
|
|
1 ö |
æ |
|
1+ jwD |
ö |
|
||||
|
|
ç |
|
÷ |
|
|||||||
Re = Reç |
|
|
|
÷ |
2 |
= |
||||||
1 |
= Reç |
÷ |
||||||||||
è |
+ jwD ø |
è |
1+ (wD) |
ø |
|
|||||||
|
|
|
= |
|
|
|
1 |
|
, |
|
|
|
|
|
|
1+ (wD)2 |
|
|
|
|
|||||
мнимая часть, соответственно, равна: |
||||||||||||
Рис.15. Преобразование s → z |
|
|
Im = |
|
|
ω |
|
, |
|
|
||
в методе обратной разности. |
|
|
1+ (wD)2 |
|
|
|||||||
43
и они удовлетворяют соотношению:
æ |
1 ö2 |
2 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
(wD)2 |
|
|||
çRe- |
÷ |
+ Im |
|
= |
|
|
|
- |
|
|
|
|
|
|
+ |
|
+ |
|
= |
|
(1+ (wD)2 )2 |
|
+ (wD)2 |
|
(1+ (wD)2 )2 |
||||||||||||||
è |
2 ø |
|
|
|
1 |
|
4 |
|
|
||||||||||
|
= |
1+ (wD)2 |
|
- |
1+ (wD)2 |
+ |
1 |
= |
1 |
|
|
|
|
|
|||||
|
|
|
|
4 . |
|
|
|
|
|||||||||||
|
(1+ (wD)2 )2 |
(1+ (wD)2 )2 |
4 |
|
|
|
|
||||||||||||
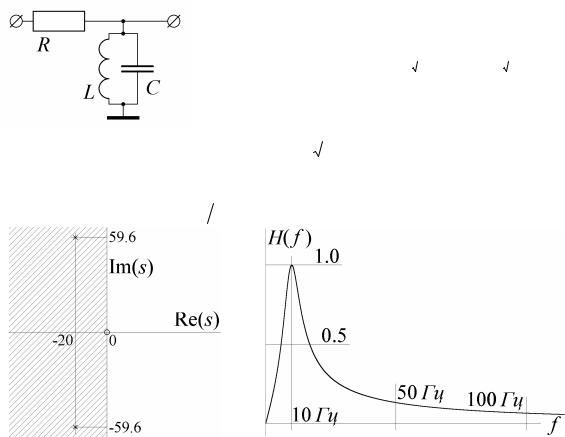
Точка s = 0 при этом отображается в точку z = 1 = e j0 , при устремлении s → ∞ точка z стремится к нулю сверху z → j0 , при s → −∞ она стремится к нулю снизу z → − j0 . При таком отображении левая полуплоскость s- плоскости отображается во внутреннюю часть малой окружности рис.16, то
есть все полюсы устойчивого аналогового фильтра отображаются заведомо во внутреннюю часть единичной окружности z-плоскости. Таким образом,
при использовании метода обратной разности устойчивость аналогового фильтра гарантирует устойчивость цифрового. Тем не менее, как и в методе прямой разности, образ мнимой оси s-плоскости совпадает с единичной ок- ружностью только в окрестности точки z = 1, то есть для совпадения частот- ных характеристик аналогового и цифрового фильтров необходимо, как и в методе прямой разности, уменьшать интервал дискретизации по времени .
Пример 12. Рассмотрим аналоговую цепь, изображенную на рис.16.
Передаточная характеристика изображенного фильтра содержит два нуля и два полюса:
|
|
|
H (s) = |
|
|
|
s |
L |
|
|
|
= |
|
|
|
|
|
s |
1 |
|
|
|
|
|
. |
||||
|
|
|
R |
|
|
|
|
|
|
|
RС |
|
|
|
|
||||||||||||||
|
|
|
|
1 + s |
L |
+ s2 LC |
|
|
|
L+ |
|
|
|
|
L− |
|
|
||||||||||||
|
|
|
|
|
|
|
L2 −4 R2LC |
|
|
|
L2 −4 R2LC |
|
|||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s + |
|
2 RLC |
|
)(s + |
|
2 RLC |
) |
|
||||
|
|
|
Выберем для определенности параметры рассматри- |
||||||||||||||||||||||||||
|
|
|
ваемой цепи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Рис.16. Непрерывная цепь |
|
|
1 |
|
= 10 Гц; |
RC = 0.025с . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2π LC |
|
|
|
||||||||||||||||||||||
второго порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При таком выборе параметров передаточная характеристики цепи принимает вид: |
|||||||||||||||||||||||||||||
H (s) = |
|
s 0.0101c |
|
= |
|
|
|
|
|
|
|
|
|
|
|
s 40 Гц |
|
|
|
|
|
|
. |
(7.3) |
|||||
|
+ s 0.0101c + s2 0.01c2 |
(4π2 ) |
(s + (20 + 59.6 j)Гц)(s + (20 − 59.6 j)Гц) |
||||||||||||||||||||||||||
1 |
|
|
|
|
|||||||||||||||||||||||||
а) |
б) |
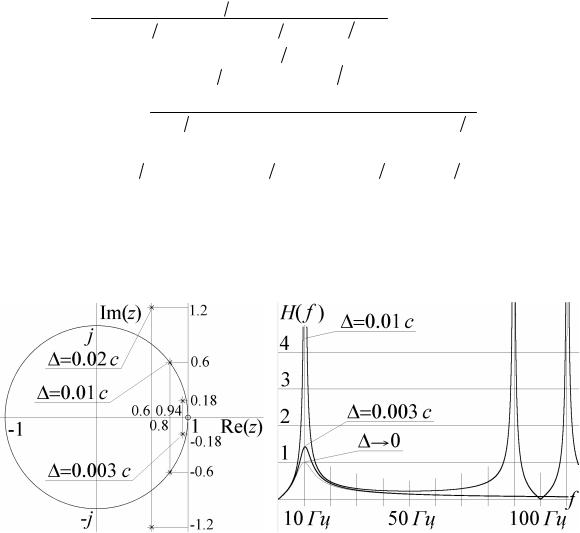
Рис.17. Расположение нулей и полюсов передаточной характеристики фильтра рис.16 (а) и его амплитудно-частотная характеристика (б)
44
Теперь передаточная характеристика имеет один нуль z = 0 и два комплексных по- люса, лежащие в ее левой полуплоскости. Расположение полюсов на s-плоскости и ампли- тудно-частотная характеристика рассматриваемого фильтра приведены на рис.17.
Применим к передаточной характеристике (7.3) метод прямой разности:
H (z) = |
|
|
|
((z −1) |
)0.0101c |
= |
|
|
|
1+ ((z −1) )0.0101c + ((z −1) |
)2 0.01c2 (4π2 ) |
|
|
||||||
= |
|
|
(z −1)(0.0101c |
) |
= |
|
|
||
|
1+ (z −1)(0.0101c |
)+ (z −1)2 0.01c2 (2π )2 |
|
(7.4) |
|||||
|
|
|
|
|
|
(z−1 − z−2 ) |
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
z−2 ( 0.0101c)+ (z−1 − z−2 )+ (1− 2z−1 + z−2 )0.025c |
||||||
= |
|
|
|
(z−1 − z−2 ) |
|
. |
|
||
|
z−2 ( 0.0101c −1+ 0.025c |
)+ z−1 (1− 0.05c |
)+ 0.025c |
|
|||||
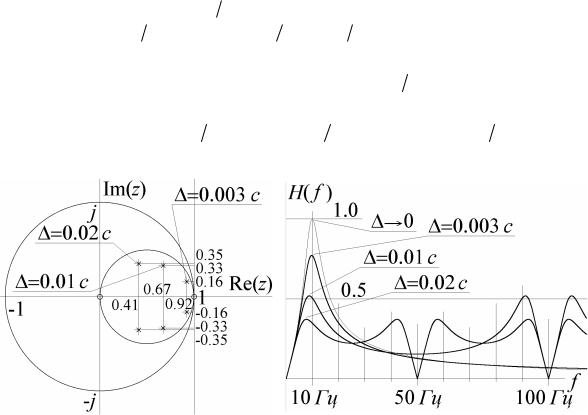
Цифровой фильтр с полученной передаточной характеристикой легко реализовать, используя прямые формы, или каким-либо другим способом. При этом выбор интервала дискретизации непосредственно влияет на расположение нулей и полюсов передаточ- ной характеристики синтезированного фильтра (так, что он может оказаться даже неус- тойчивым), а также на форму его частотной характеристики. На рис.18 изображено распо- ложение нулей и полюсов и амплитудно-частотная характеристика синтезированного фильтра при различных значениях интервала дискретизации.
а) б)
Рис.18. Расположение нулей и полюсов передаточной характеристики (7.4) (а) и АЧХ соответствующего цифрового фильтра (б) при различных значениях .
При выборе = 0.02 c передаточная характеристика цифрового фильтра содержит
полюсы вне единичной окружности, поэтому говорить о частотной характеристике в этом случае не имеет смысла. Выбор = 0.01c обеспечивает положение полюсов внутри ок-
ружности, однако они лежат очень близко к ней, поэтому форма АЧХ цифрового фильтра лишь отдаленно напоминает АЧХ исходного непрерывного фильтра. При таком значении период частотной характеристики цифрового фильтра должен равняться 100 Гц, что на- глядно демонстрирует рис.17б. При = 0.003c форма АЧХ уже достаточно близка к тре-
буемой. Дальнейшее уменьшение интервала дискретизации приводит к тому, что АЧХ
цифрового фильтра все больше и больше стремится к АЧХ непрерывного прототипа и в пределе совпадает с ней, что показано тонкой линией на рис.18б.
Как явственно следует из примера, выбор достаточно маленького зна- чения интервала дискретизации обеспечивает устойчивость синтезированно- го цифрового фильтра.
45
Пример 13. Применим к непрерывному фильтру рис.16 метод обратной разности.
Для этого сделаем в выражении (7.3) замену (7.2): |
|
|
|
|
|
||||||||
H (z) = |
|
|
|
|
|
((1 − z−1 ) |
) 0.0101c |
|
|
= |
|
|
|
|
1 + ((1 |
− z−1 ) |
)0.0101c + ((1 − z−1 ) )2 0.01c2 |
(4π2 ) |
|
|
|
||||||
|
= |
|
|
|
(1 − z−1 )0.0101c |
|
|
|
= |
|
(7.5) |
||
|
|
(1− z−1 ) |
0.0101c + (1 − 2z−1 + z−2 ) |
|
|
|
|||||||
|
+ |
0.0002533c2 |
|
||||||||||
|
|
|
|
= |
|
|
(1 − z−1 )1c |
|
|
|
. |
|
|
|
|
|
|
z−2 0.025c2 |
− z−1 (1c + 0.05c2 |
) |
+ 100 +1c + 0.025c2 |
|
|||||
Расположение нулей и полюсов получившегося при этом цифрового фильтра, а также его АЧХ при различных значениях интервала дискретизации приведены на рис.19.
а) б)
Рис.19. Расположение нулей и полюсов передаточной характеристики (7.5) (а) и АЧХ соответствующего цифрового фильтра (б) при различных значениях .
Как и в примере 12, уменьшение интервала дискретизации приводит к все больше- му приближению АЧХ цифрового фильтра к АЧХ непрерывного прототипа. Как и на рис.18б, на рис.19б тонкой линией изображена АЧХ непрерывного фильтра, к которой стремиться АЧХ цифрового фильтра при уменьшении интервала дискретизации. Частот- ная характеристика цифрового фильтра, естественно, обладает периодичностью с перио- дом 1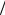 . Синтезированный цифровой фильтр, как уже отмечалось, остается устойчивым
. Синтезированный цифровой фильтр, как уже отмечалось, остается устойчивым
при любом выборе интервала дискретизации, поскольку его полюсы заведомо лежат внут- ри единичного круга. Некоторое недоумение может вызвать наличие дополнительного по- люса в точке z = 0 . Этот факт, впрочем, легко объяснить тем, что исходная передаточная характеристика (7.3) стремится к 0 при s → ∞ , из чего следует, что передаточная характе- ристика полученного цифрового фильтра будет стремиться к 0 при z → 0 .
Методы прямой и обратной разностью дают удовлетворительный ре- зультат только при выборе достаточно малого значения интервала дискрети- зации. Это связано в первую очередь с тем, что образ мнимой оси s- плоскости не совпадает с единичной окружностью z-плоскости. Поэтому ак- туальным остается поиск преобразования s → z , отвечающего всем сформу- лированным условиям. Хотя, даже если это преобразование будет отвечать всем условиям, частотная характеристика цифрового фильтра не может сов- падать с частотной характеристикой аналогового прототипа, поскольку пер- вая является периодичной, а вторая – нет.
46
Знакомство с методами вычислительной математики наталкивает на мысль использовать симметричную аппроксимацию производной:
dx → |
xn +1 − xn −1 |
. |
|
|
||
dt |
2 |
|
|
|
|
|
Такая аппроксимация приводит к преобразованию: |
|
|
||||
s → |
z − z−1 |
. |
|
|
|
|
2 |
|
|
|
|||
|
|
Однако использование |
симметрич- |
|||
|
|
|
||||
|
|
ной аппроксимации производной приво- |
||||
|
|
дит к тому, что левая полуплоскость s- |
||||
|
|
плоскости преобразуется в многосвяз- |
||||
|
|
ную область z-плоскости, как это пока- |
||||
|
|
зано на рис.20. При этом каждая точка s- |
||||
|
|
плоскости переходит в две точки z- |
||||
|
|
плоскости, так что преобразование даже |
||||
|
|
не сохраняет количества нулей и полю- |
||||
|
|
сов |
|
передаточной |
характеристики. |
|
|
|
Мнимая ось s-плоскости отображается |
||||
|
|
сразу на единичную окружность и на |
||||
|
|
мнимую ось z-плоскости, а точка s = ∞ – |
||||
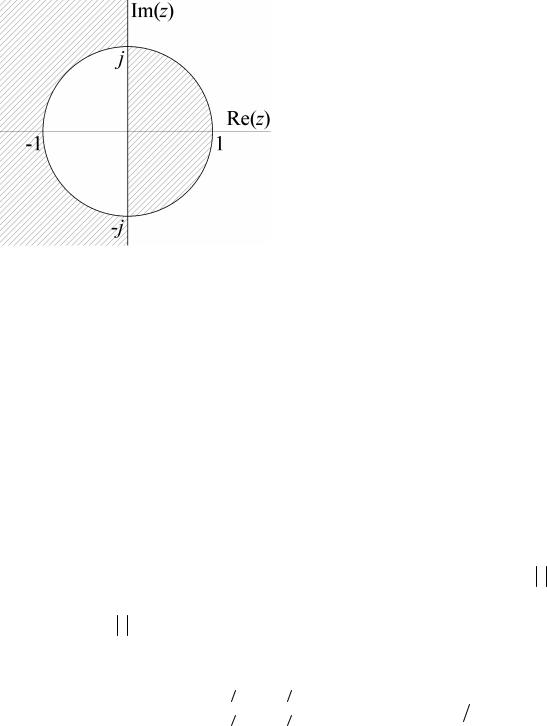
Рис.20. Преобразование s → z при |
одновременно в две |
точки |
– z = ∞ и |
|||
использовании симметричной |
z = 0 . |
|
|
|||
разностной аппроксимации. |
|
Таким образом, применение симмет- |
||||
ричной разностной аппроксимации не приносит ожидаемых результатов. Это же можно сказать и об аппроксимациях более высоких порядков.
Тем не менее, известно и широко используется преобразование s → z , удовлетворяющее всем необходимым требованиям. Это так называемое би-
линейное преобразование: |
2 1− z−1 |
|
|
||||||
s → |
. |
(7.6) |
|||||||
|
|
|
|
|
|
||||
|
1 |
+ z−1 |
|||||||
|
|
|
|
||||||
Выражение (7.6) допускает обращение: |
|
||||||||
z ← |
2 |
|
+ s |
, |
|
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
||||
2 |
|
− s |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
из вида которого легко сделать вывод, что точки мнимой оси s = jω били- нейное преобразование переводит в точки единичной окружности z = 1, а точки левой полуплоскости Re(s)< 0 – в область, ограниченную единичной окружностью z < 1.
Итак, |
точка s = jω s-плоскости |
|
должна преобразовываться |
в точку |
|||||||||||||
z = e jϕ z-плоскости: |
|
|
|
|
|
|
|
|
2 jsin ϕ2 |
|
|
|
|
||||
jω → |
|
2 1 |
− e− jϕ |
= |
2 e jϕ 2 |
− e− jϕ 2 |
= |
|
2 |
|
= |
2 |
j tg(ϕ 2). |
(7.7) |
|||
|
|
1 |
+ e− jϕ |
|
e jϕ 2 |
+ e− jϕ 2 |
|
2cos ϕ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
47
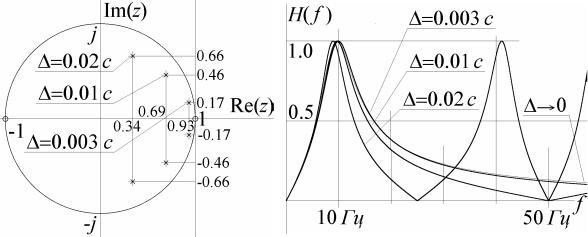
Полученное преобразование позволяет сделать вывод, что величина tgϕ, где ϕ – аргумент точки единичной окружности z-плоскости, соответству- ет параметру ωΔ, где ω – частота частотной характеристики непрерывного фильтра. В частности, бесконечно большая частота ω → ±∞ в частотной ха- рактеристике непрерывного фильтра соответствует частоте ± π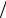 в частот- ной характеристике полученного цифрового фильтра.
в частот- ной характеристике полученного цифрового фильтра.
Пример 14. Применим билинейное преобразование к непрерывному фильтру рис.16 с передаточной характеристикой (7.3). Для этого подставим в (7.3) выражение (7.6):
|
|
|
|
|
|
|
|
|
2 1 - z−1 |
0.0101c |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H (z) = |
|
|
|
|
|
|
|
|
D 1 + z−1 |
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 1 - z−1 |
|
|
2 1- z−1 |
ö2 |
|
|
||||||||||||
|
|
|
æ |
2 |
|
|
|
|||||||||||||
1 + |
|
|
|
|
|
0.0101c + ç |
|
|
|
|
÷ 0.0002533c |
|
|
|
|
|||||
|
|
|
|
−1 |
|
|
|
−1 |
|
|
|
|
||||||||
|
|
|
D 1 + z |
ç |
|
|
|
÷ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
è D 1 + z |
|
ø |
|
|
|
|
|||||||
|
= |
|
|
|
|
|
|
|
|
|
D (1 + z−1 )(1 - z−1 )0.0202c |
|
|
= |
(7.8) |
|||||
|
D2 (1 + z−1 )2 + D (1 + z−1 )(1 - z−1 )0.0202c + (1 - z−1 )2 0.0010132c2 |
|||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
D (1 - z−2 ) |
|
|
|
= |
|
|
|
|
|
D2 (1 + 2z−1 + z−2 ) 49.5 Гц + D (1 - z−2 ) |
+ (1 - 2z−1 + z−2 ) 0.0502c |
||||||||||||||
|
|
D (1 - z−2 ) |
|
= |
|
|
. |
z−2 (D2 49.5 Гц - D + 0.0502c) |
+ z−1 (D2 99 Гц - 0.1004c) + D2 49.5 Гц + D + 0.0502c |
||
На рис.21 приведено расположение нулей и полюсов цифрового фильтра, получен-
ного после применения билинейного преобразования к передаточной характеристике (7.3), а также его АЧХ при различных значениях интервала дискретизации.
а) |
б) |
Рис.21. Расположение нулей и полюсов передаточной характеристики (7.8) (а) и АЧХ соответствующего цифрового фильтра (б) при различных значениях D.
Как и следовало ожидать, и что прекрасно демонстрирует рис.21б, метод билиней- ного преобразования приводит к гораздо лучшей аппроксимации исходной частотной ха- рактеристики, поскольку он отображает мнимую ось s-плоскости непосредственно в еди- ничную окружность z-плоскости. Как и в примере 13, передаточная характеристика полу- ченного цифрового фильтра содержит дополнительный нуль z = −1, поскольку именно эта точка соответствует точке s-плоскости s → ∞ . Точка z = −1, однако, лежит непосред- ственно на единичной окружности, поэтому частотная характеристика цифрового фильтра
48
обращается в ноль на частоте ω = π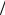 , или f = ω
, или f = ω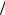 (2π) = 1
(2π) = 1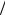 (2 ), что отчетливо видно на
(2 ), что отчетливо видно на
рис.21б.
Итак, методы отображения дифференциалов позволяют по передаточ- ной характеристике непрерывного фильтра построить цифровой фильтр. При
этом абсолютно точного совпадения частотных характеристик непрерывного и цифрового фильтров добиться невозможно, наилучшие результаты дости- гаются при использовании билинейного преобразования. При устремлении к
нулю интервала дискретизации частотная характеристика цифрового фильтра стремится к частотной характеристике непрерывного фильтра.
Сформулируем последовательность действий при использовании мето- дов отображения дифференциалов.
1)Исходными данными является передаточная характеристика непре- рывного прототипа проектируемого фильтра.
2)В передаточной характеристике непрерывного фильтра производит-
ся замена |
s → |
2 1 |
− z−1 |
(либо, по |
каким-либо причинам, одна из замен |
||||||||
|
|
+ z−1 |
|||||||||||
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
s → |
z −1 |
|
|
1− z−1 |
|
z − z−1 |
|
||||||
|
|
, |
s → |
|
|
|
|
, или s → |
|
). |
|||
2
3) По полученной передаточной характеристике строится цифровой фильтр.
49
