Цифровая обработка сигналов (сборник книг) / Белодедов М.В. Методы проектирования цифровых фильтров, 2004

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Полтавский национальный технический университет им. Ю. Кондратюка

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

X (w) = åxne− jωn

.pdf

Скачиваний:

Добавлен:

05.03.2016

Размер:

902.07 Кб

Скачать

☆

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

казать, что задержка на N отсчетов приводит к умножению z-преобразования на z− N .

3) Z-преобразование свертки сигналов. Рассмотрим свертку дискретных сигналов:

∞

x Ä y : åxn′ yn −n′ , n′=−∞

которая является дистрибутивной операцией, то есть не изменяется при пере- становке операндов:

∞	∞	∞	∞	∞
åxn′ yn −n′ =	åxn −n′′ yn′′ =	åxn −n′′ yn′′ =	åxn −n′′ yn′′ = åxn −n′ yn′ : y Ä x .
n′= −∞	n′=−∞	n −n′′=−∞	n′′= −∞	n′= −∞
Вычислим z-преобразование свертки:
∞ ∞		∞ ∞		∞	∞
Z[x Ä y]= å åxn′ yn −n′ z−n = å åxn′ yn −n′ z−n =				å xn′	å yn −n′ z−n
n = −∞ n′= −∞		n′= −∞ n =−∞		n′= −∞	n =−∞	(1.8
∞		∞				(1.8
∞		∞
= åxn′z−n′Y (z) = Y (z) åxn′ z−n′ = Y (z)X (z) = Z[x]Z[y].						)
n′= −∞		n′=−∞

Таким образом, z-преобразование свертки двух сигналов представляет собой произведение z-преобразований сигналов, входящих в свертку.

4) Связь z-преобразования со спектром сигнала.

Спектр дискретного сигнала (1.2) легко может быть получен из его z- преобразования:

то есть спектр сигнала представляет собой значения его z-преобразования,

взятые в точках z = e jω , которые лежат на окружности единичного радиуса, причем параметр ω является полярным углом точки на окружности. Сде- ланный вывод в очередной раз свидетельствует, что спектр дискретного сиг- нала обязан быть периодичным с периодом 2π .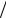

На этом этапе рассуждений полезно вновь обратиться к примеру 2 и рассмотреть его с новой точки зрения. При a < 1 единичная окружность ле-

жит в области сходимости z-преобразования и поэтому функция X (z) опре- делена в каждой ее точке, то есть определен и спектр исходного сигнала. Ес- ли же a > 1, то единичная окружность лежит вне области сходимости и

спектр сигнала не определен, что легко понять, поскольку в этом случае сам дискретный сигнал не является ограниченным.

Контрольные вопросы и задачи.

1. Какова максимальная погрешность при дискретизации непрерывного сигнала, принимающего значения в диапазоне (−1) ÷ (+1) В, 12-разрядным АЦП?

2.Непрерывной или дискретной функцией частоты является спектр дискретного сигнала (1.2)?

3.Вычислите максимально возможный интервал дискретизации при дискретизации сигнала с полосой частот (20 Гц ÷ 20 кГц).

4.Вычислите спектр дискретного сигнала:

ì1	при	0 ≤ n ≤ N;
xn = í	при	n < 0, n > N.
î0	при	n < 0, n > N.

5. Исследуйте, как различаются дискретные спектры одного и того же сигнала, отсчеты которого взяты с разными интервалами дискретизации:

	∞
	X1(w) = åx(nD)e− jωn ;
	n=−∞	(1.2)
	∞	(1.2)
	∞
	X2 (w) = åx(n ´ 2D)e− jωn×2 .
	n=−∞

6. Вычислите z-преобразование сигнала с 4 отличными от нуля отсче- тами: x0 = 1, x1 = 1, x2 = 0,5, x3 = 0,25. Какова область сходимости этого z-

преобразования?

7. Вычислите z-преобразование сигнала:

ì0	при n < 0;
x: xn = í	при n ³ 0.
îAcos(wnD)	при n ³ 0.

Сравните полученный результат с примером 3.

8.Вычислите z-преобразование сигнала x2n , считая известным z- преобразование сигнала xn .

9.Вычислите z-преобразование сигнала:

ì1 при четных n;

x: xn = íî-1 при нечетных n.

10. Обладает ли свойством симметрии спектр дискретного сигнала, от- счеты которого принимают комплексные значения?

2. Цифровые фильтры.

Начнем теперь рассмотрение систем, выполняющих обработку дис- кретных сигналов. По аналогии с непрерывными системами их логично на- зывать фильтрами. В настоящее время такие системы принято называть циф- ровыми фильтрами (digital filters). Обработка сигнала в самом общем случае может быть выражена как некоторый алгоритм, или закон, позволяющий по заданному входному сигналу x получить выходной сигнал y. Этот алгоритм удобно выразить соотношением:

y = ˆ[x]

L ,

где через ˆ обозначен оператор, отображающий пространство дискретных

сигналов само на себя и присущий данному конкретному цифровому фильт- ру.

Будем рассматривать далее линейные фильтры, то есть фильтры, реак- ция которых (выходной сигнал) на сумму двух входных может быть пред- ставлена как сумма его реакций на отдельные составляющие входного сигна- ла:

ˆ	ˆ	ˆ	]	ˆ	ˆ	].
L[ax1	+ bx2 ]= L[ax1	]+ L[bx2	]	= aL[x1	]+ bL[x2	].
Кроме того, выделим в отдельную группу фильтры, реакция которых

на сдвинутый по времени сигнал представляет собой сдвинутую по времени на такую же величину реакцию фильтра на несдвинутый сигнал:

~	ˆ	]= y,
Если xn = xn−N и L[x		]= y,
ˆ ~	~
то L[x	]= y : yn−N .

Такие фильтры будем называть инвариантными. Для дискретных сиг- налов, отсчеты которых относятся к разным моментам времени, требование инвариантности является естественным и не требующим специального по- стулирования. Это связано с тем фактом, что время, как правило, не имеет выделенной точки отсчета. Существуют, однако, такие дискретные системы, в которых требование инвариантности далеко не так естественно. Такие сис- темы встречаются, например, в случае, если отсчеты дискретного сигнала от- носятся не к различным моментам времени, а к различным точкам простран- ства.

Далее мы будем рассматривать линейные инвариантные фильтры.

Именно для таких фильтров удается получить ряд достаточно интересных выводов, оказывающихся весьма полезными при анализе и синтезе дискрет- ных систем.

Рассмотрим воздействие на линейный инвариантный фильтр единично- го сигнала e. Обозначим выходной сигнал фильтра при таком воздействии как h и будем называть его импульсной характеристикой:

ˆ[e]= h

L .

Для линейных инвариантных фильтров импульсная характеристика полностью характеризует фильтр. Чтобы показать это, представим произ- вольный входной сигнал как его свертку с самим собой:

∞	∞
x = x Äe : xn = åen′ xn −n′ = åen −n′ xn′ .
n′= −∞	n′=−∞
В последнем выражении величины	xn′ являются просто числами (не

сигналами), поэтому воздействие линейного инвариантного цифрового фильтра на входной сигнал может быть записано следующим образом:

	ˆ	∞
	ˆ	åhn−n′ xn′ ,
	L[x]= y : yn =	åhn−n′ xn′ ,
		n′=−∞

то есть выходной сигнал линейного инвариантного фильтра может быть вы- ражен как свертка входного сигнала и импульсной характеристики:

ˆ	(2.1)
y = L[x]= x Ä h.

Реальные цифровые фильтры, обрабатывающие временные дискретные сигналы, должны отвечать принципу причинности, запрещающему выходно- му сигналу принимать отличные от нуля значения до прихода первого нену- левого отсчета входного сигнала. Такие фильтры будем называть каузальны- ми фильтрами, их импульсная характеристика должна подчиняться требова- нию:

hn = 0 при n < 0 .

(2.2)

Отметим, что требование каузальности, столь естественное для вре- менных фильтров, совершенно не имеет место, например, при рассмотрении дискретных сигналов, описывающих пространственные распределения ка- кой-либо величины.

Воспользуемся теперь одним из рассмотренных свойств z- преобразования и выполним z-преобразование обеих частей равенства (2.1):

Z[y]=Y (z)= Z[x Ä h]= Z[x]Z[h]= X (z)H(z).

Таким образом, z-преобразование выходного сигнала фильтра может быть получено из z-преобразования входного сигнала путем домножения его на функцию H(z), которая носит название передаточная характеристика

цифрового фильтра. По определению, передаточная характеристика равна z- преобразованию импульсной характеристики. Подчеркнем, что передаточной характеристикой обладают только линейные инвариантные фильтры.

При рассмотрении непрерывных сигналов и непрерывных фильтров важную роль играет частотная характеристика, определяемая как отноше-

ние амплитуд входного и выходного сигналов фильтра при воздействии на него гармоническим сигналом определенной частоты. Определим подобным же образом частотную характеристику цифрового фильтра. Подадим на вход

линейного инвариантного фильтра абстрактный гармонический сигнал xn = Ae jω0 n . Выходной сигнал фильтра легко вычислить:

X (z)= Ad(z - e jω0 );

Y (z)= X (z)H(z)= Ad(z - e jω0 )H(z)= AH(e jω0 )d(z - e jω0 ); yn = AH(e jω0 )e jω0n ,

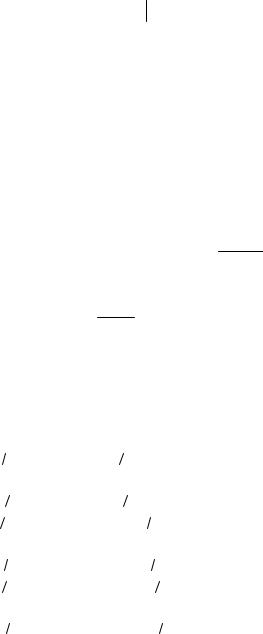
и он также является гармоническим сигналом, причем отношение амплитуд выходного и входного сигнала определяется значением передаточной харак- теристики фильтра в точке единичной окружности, соответствующей частоте входного сигнала. Итак, частотная характеристика линейного инвариантного

цифрового фильтра равна значению передаточной характеристики фильтра в соответствующей точке:

H (ω) = H(z)z=e jω .

Определенная таким образом частотная характеристика совпадает со спектром импульсной характеристики, как это и имеет место в случае непре- рывных систем:

H (ω) = H(z)	∞	∞

	z =e jω0 = åhn z−n	= åhne− jω0n .

	n =−∞	z =e jω0 n =−∞

Рассмотрим в качестве примера цифровой фильтр, осуществляющий численное дифференцирование входного сигнала и работающий по следую- щему алгоритму: yn = (xn − xn −1 ) . Для вычисления передаточной характе-

ристики фильтра выполним z-преобразование последнего равенства:

Y (z)= (X (z)− z−1X (z))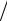 = X (z)1− z−1 ,

откуда:

H(z) = YX((zz)) = 1− z−1 .

Зная передаточную характеристику, найдем частотную характеристику:

H (ω) = H(z)	z =e	jω = 1− e− jω	,

используя которую, можно по формуле (1.4) вычислить отсчеты импульсной характеристики:

h =

H (ω)dω =

1− e− jω

dω =

;

2π

2π ò

−π

e jω −1dω = −

h1 =

òH (ω)e jω dω =

; .

2π

−π

h =

H (ω)e2 jω

dω =

e2 jω − e jω

dω = 0;

2π

2π ò

−π

= 0;

h4 = 0;

...

Таким образом, только два отсчета импульсной характеристики рас- сматриваемого фильтра отличны от нуля. Этот же результат можно было по- лучить, проанализировав реакцию фильтра на единичный сигнал:

hn = (en − en−1 );

h =

(e0 − e−1 )

;

h =

(e1 − e0 )

= -

;

(e2 − e1 )

= 0;

h = 0;

= 0; ...

Рассмотрим теперь каузальный линейный инвариантный цифровой фильтр. Для него передаточная характеристика запишется несколько более простым образом:

∞	∞
H(z) =Z[h]= åhn z−n = åhn z−n .		(2.3)
n =−∞	n =0

Поскольку выражение (2.3) является степенным рядом [Г.Е.Шилов. Ма-

тематический анализ (функции одного переменного). – М.: Наука, 1969, с.239], сущест-

вует некий радиус его сходимости R, при этом ряд (2.3) сходится во всех точ- ках z-плоскости, для которых z > R , и расходится во всех точках с z < R .

Можно, поэтому, утверждать, что, если передаточная характеристика не оп- ределена в какой-либо точке z = p , она не определена также во всех точках

z < p .

Пример 5. Пусть цифровой фильтр имеет импульсную характеристику

ì	n	при	n ³ 0;
hn = ía		при	n ³ 0;
î0		при	n < 0.

Передаточная характеристика такого фильтра имеет вид (см. пример 2):

H (z) = -1 −1 . 1 az

Последнее выражение не определено в точке z = a . Из этого следует, что переда- точная характеристика не определена также во всех точках z < a , как это уже отмечалось

в примере 2. При воздействии на фильтр произвольным сигналом x z-преобразование вы- ходного сигнала Y (z) также не будет определено в точках z < a . Если a > 1, то Y (z) не

будет определено и на единичной окружности, следовательно, выходной сигнал не будет иметь спектра и не будет ограниченным.

Будем называть устойчивыми цифровыми фильтрами такие фильтры, выходной сигнал которых при ограниченном входном сигнале также являет- ся ограниченным. Поскольку при перемножении двух z-преобразований об- ласть сходимости может только уменьшаться, нетрудно показать, что необ- ходимым и достаточным условием устойчивости является требование R < 1, где R – радиус сходимости передаточной характеристики цифрового фильт- ра.

Рассмотренный в примере 5 цифровой фильтр является устойчивым при a < 1 и неустойчивым в противном случае.

Напомним, что полученные результаты касаются только каузальных цифровых фильтров и применение их к некаузальным фильтрам требует ос- мотрительности.

Как для преобразования Фурье существует обратное преобразование, так его имеет и z-преобразование:

xn = ò X (z)zn −1dz ,

(2.4)

где контур интегрирования лежит в области сходимости и охватывает точку z = 0 .

На практике применение формулы (2.4) приводит к громоздким вы- кладкам. Как правило, вычислить обратное z-преобразование обычно удается более простыми способами.

Пример 6. Вычислим реакцию цифрового фильтра с каузальной импульсной ха- рактеристикой hn = an sin(w0nD) на гармонический сигнал xn = bn , начинающийся в мо-

мент времени 0.

Поскольку импульсную характеристику можно представить в виде:

hn = an e jω0n - e− jω0n

(ae jω0

)n -

(ae− jω0 )n ,

2 j

легко найти передаточную характеристику фильтра:

H(z) =

ú .

- ae

jω0

−1

1 - ae

− jω0

−1

2 j ë1

Зная передаточную характеристику и z-преобразование входного сигнала:

X (z) =

1- bz−1

найдем z-преобразование выходного сигнала фильтра:

Y (z) = H(z)X (z) =

2 j

- ae

jω0

−1

1 - ae

− jω0

−1

ë1

û 1 - bz

ú.

- ae

jω0

−1

1 - bz

−1

- ae

− jω0

−1

1- bz

−1

2 j ë1

Пользуясь стандартной методикой, представим произведение дробей в виде их суммы:

Y (z) =

ae jω0

jω0

- b 1 - ae

jω0

−1

jω0

- b 1- bz

−1

2 j ëae

ae− jω0

ú.

− jω0

- b 1 - ae

− jω0

−1

− jω0

- b 1 - bz

−1

Каждое слагаемое в полученном выражении представляет собой z-преобразование показательной последовательности из примера 5, поэтому выполнить обратное z- преобразование очень легко:

ae jω0

an e jω0n

ae− jω0

an e− jω0n +

yn =

bn -

bn ú

2 j

jω0

- b

jω0

- b

− jω0

- b

− jω0

- b

ëae

e jω0 (n +1)

e− jω0 (n +1) ö

öù

an +1ç

+ bn +1

÷ú

jω0

− jω0

jω0

- b ae

- b

2 j ë

è ae

- b ø

è ae

øû

asin(w D)(an +1 + bn +1 )- an +1bsin(w (n +1)D)

a2 - 2abcos(w D)+ b2

Полученное выражение справедливо только при n ³ 0 . При n < 0 , как это следует из примера 5, отсчеты выходного сигнала должны иметь нулевое значение.

Таким образом, путем не очень сложных выкладок нам удалось получить точный вид выходного сигнала рассматриваемого фильтра. Интересно отметить, что, несмотря на обилие комплекснозначных промежуточных результатов, выходной сигнал оказывается чисто действительным, каким он, собственно, и должен быть при действительном вход- ном сигнале и действительной импульсной характеристике.

Контрольные вопросы и задачи.

1. Чему равна импульсная характеристика цифрового фильтра, задер- живающего входной сигнал на N отсчетов: yn = xn−N ? Обладает ли она свой-

ствами инвариантности и каузальности?

2. Может ли цифровой фильтр обладать симметричной импульсной ха- рактеристикой: h−n = hn ?

3. Найдите импульсную характеристику цифрового фильтра yn = (xn − 2xn−1 − xn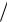−2 ) 2 .

4.Найдите реакцию фильтра yn = (xn + xn−1 )2 на единичный сигнал. Яв- ляется ли эта реакция импульсной характеристикой?

5.Найдите импульсную характеристику цифрового фильтра yn = xn n .

6.Возможен ли цифровой фильтр с передаточной характеристикой

H(z) = 1+ z2 + z−2 ?

7.Найдите импульсную характеристику цифрового фильтра с переда-

точной характеристикой H(z) =	z2
		.
	1+ 2z2


8.	Является ли устойчивым цифровой фильтр с передаточной характе-
ристикой H(z)=		z2
			?
		1+ 2z2
9.	Два цифровых фильтра с каузальными импульсными характеристи-

ками hn(1) = an и hn(2) = bn соединяются последовательно – выход первого под-

ключается ко входу второго. Найдите импульсную характеристику получив- шегося цифрового фильтра.

10. Возможен ли цифровой фильтр с областью сходимости R1 < z < R2 ?

3. Цифровые фильтры с сосредоточенными параметрами.

Рассмотрим отдельные элементы, являющиеся «строительным набо- ром» для построения цифровых фильтров.

1. Сумматор – устройство с двумя (или бо-
лее) входами и одним выходом. Выходной сигнал
представляет собой сумму двух входных:
y = x(1) + x(2) .
Сумматор является линейным устройством, поскольку	если
y (1) = x(1) + x(2) и y (2) = x(3) + x(4) то
y = a(x(1) + x(2))+ b(x(3) + x(4))= ay(1) + by(2) .

Так же без каких-либо затруднений можно показать, что сумматор яв- ляется инвариантной системой.

2. Умножитель на коэффициент. Выходной сиг- нал представляет собой входной, умноженный на не- который, как правило, действительный, коэффициент:

y = ax .

Умножитель также является линейным инвариантным устройством. Его передаточная характеристика определена на всей z-плоскости и равна ко- эффициенту a: H(z)= a .

3. Элемент задержки. Выходной сигнал пред- ставляет собой входной, задержанный на один отсчет:

yn = xn −1 .

Такой элемент, конечно, линеен и инвариантен. Как уже было показа- но, его передаточная характеристика равна выражению: H(z) = z−1 и опреде- лена везде, за исключением точки z = 0 .

Рассмотренные элементы являются линейными, инвариантными и кау- зальными. Поэтому этими же качествами будет обладать любая их комбина- ция, то есть такое соединение, при котором выходы одних элементов под- ключаются ко входам других.

Будем называть устройство, представляющее собой комбинацию ко- нечного числа элементов рассмотренных трех типов, цифровым фильтром с сосредоточенными параметрами. Рассмотрим вопрос о передаточной харак- теристике фильтра с сосредоточенными параметрами с одним входом x и од- ним выходом y. Обозначим выходные сигналы элементов задержки, входя-

щих в состав фильтра, символами q(k ). Так как на вход этих элементов за-

держки может поступать только линейная комбинация других сигналов q(k ) и, возможно, входного сигнала x, можно записать:

K
qn(k ) = åak ,mqn(m−1) + bk xn−1, k = 1,..., N .	(3.1)

m=1

Выходной сигнал фильтра, конечно, также будет определяться линей- ной комбинацией этих же сигналов:

K
yn = åa0,mqn(m) + b0 xn .	(3.1а)

m=1

Вn-ный момент времени состояние фильтра полностью определяется

набором параметров qn(1),...,qn(K ), то есть вектором в K-мерном пространстве.

По этой причине разбираемый метод анализа цифровых фильтров с сосредо- точенными параметрами обычно называется методом пространства со-

стояний.

Выполним z-преобразование выражений (3.1) и (3.1а):

Q(k )(z)= åak ,m z−1Q(m)(z)+ bk z−1X (z),

k =1,..., N ;

(3.2)

m=1

(

(m)(

b0 X

(

)

(3.2а)

åa0,mQ

z .

m=1

Полученное выражение (3.2) можно рассматривать как систему линей-

ных уравнений относительно неизвестных Q(k )(z):

ì(a1,1z−1 -1)Q(1)

+ a1,2 z−1Q(2) + a1,3z−1Q(3) + ... + a1,K z−1Q(K )

= -b1z−1 X

ïa2,1z−1Q(1)

+ (a2,2 z−1 -1)Q(2) + a2,3z−1Q(3) + ... + a2,K z−1Q(K )

= -b2 z−1X

+ a3,2 z−1Q(2) + (a3,3z−1 -1)Q(3) + ... + a3,K z−1Q(K )

−1Q(1)

= -b3z−1X .

(3.3)

ía3,1z

ï ...

...

+ aK ,2 z−1Q(2) + aK ,3z−1Q(3) + ... + (aK ,K z−1 -1)Q(K ) = -bK z−1X

ïaK ,1z−1Q(1)

Определитель системы (3.3) является полиномом степени не меньше K аргумента z−1: P0 (z−1 ), а ее общее решение имеет вид:

Q(k )(z)=	P (z−1 )		X (z), k =1,..., K ,
	k			(3.4)
	P	(z−1 )
0

где Pk (z−1 ) – также полином аргумента z−1 степени не меньше K. Полученное

решение (3.4) позволяет выписать парциальные передаточные характери-

стики фильтра:

H(k )(z)=	Q(k )(z)	=	Pk	(z−1 )	, k =1,...,K ,	(3.5)
	X (z)		P0	(z−1 )

и найти z-преобразование выходного сигнала фильтра (используя соотноше-

ние (3.2а)):

Pk (z

−1

)

Y (z)= åa0,mQ(m)(z)+ b0 X (z)= åa0,m

X (z)+ b0 X (z)=

−1 )

m=1

P (z−1 )

X (z)

(z−1 )+ b P

(z−1 )÷

= X (z)

P (z−1 )

0,m k

0 0

èm=1

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

Соседние файлы в папке Цифровая обработка сигналов (сборник книг)

#
05.03.2016902.07 Кб93Белодедов М.В. Методы проектирования цифровых фильтров, 2004.pdf
#
05.03.2016863.2 Кб83Граничин О.Н. Введения в методы стохастической оптимизации и оценивания, 2003.pdf
#
05.03.2016958.12 Кб113Дронов С.В. Многомерный статистическийц анализ, 2003.pdf
#
05.03.2016109.31 Кб74Лазарев С. Быстрое Преобразование Ффурье,1999.pdf
#
05.03.20162.18 Кб56Цифровая обработка сигналов (сборник книг).txt