
SPD_Lektsii / СПД Лекция 3
.pdf
Навчальна дисципліна |
Системи передачі даних |
|
Модуль 1 |
|
Завадостійке кодування |
Змістовий модуль № 1 |
Коректувальні коди в однобічних системах передачі даних |
|
Тема 3 |
|
Циклічні коди |
Лекція № 3 |
Циклічні коди |
|
ПЛАН ЛЕКЦІЇ
Навчальні питання:
1.Загальні відомості про циклічні коди.
2.Кодування та декодування циклічного коду.
3.Вибір утворюючого поліному.
4.Мажоритарне декодування блокових кодів.
5.Неалгебраїчні методи декодування ЦК.
6.Технічні засоби кодування та декодування ЦК.
Навчально-матеріальне забезпечення:
1.ПЕОМ, мультимедійний проектор.
2.Презентація у форматі PowerPoint.
Навчальна література:
1.Воробієнко П.П., Нікітюк Л.А., Резніченко П.І. Телекомунікаційні та інформаційні мережі: Підруч. для ВНЗ. – К.: Саммит-книга, 2010. – С. 62–94.
2.Олифер В.Г., Олифер H.A. Компьютерные сети. Принцип, технологии, протоколы: Учебник для вузов. 4-е изд. – СПб.: «Питер», 2010. – С. 118–156.
1. Загальні відомості про циклічні коди.
Циклічний код являє собою різновид групового коду та не відрізняється від нього за рівнем завадозахищеності, однак завдяки простоті технічної реалізації знайшов широке застосування. Циклічні коди незамінні при необхідності передавати інформацію в каналах зв’язку, у яких відсутня можливість повторної передачі даних. Циклічні коди застосовуються при записі та зчитуванні на HDD, CD і DVD, при використанні
USB-портів для обміну інформацією, при передачі аудіота відеоінформації. Серед усього різноманіття групових кодів можна вибрати такі, в яких рядки
зв’язані умовою циклічності, тобто всі рядки матриці, що називається утворюючою, можуть бути отримані циклічним зсувом одного рядка. Зсув здійснюється справа на ліво, а крайній лівий символ переміщається в кінець рядка, тобто в крайнє праве положення. Приклад одержання первинного запису представлений на рис. 1.
Коди, у яких рядки матриці задовольняють цій умові, називаються циклічними. Будь-які «k» рядків цієї матриці лінійно незалежні та можуть бути основою для одержання будь-якої дозволеної кодової комбінації циклічного коду. Число можливих циклічних кодів істотно менше числа групових кодів. Циклічні коди мають наступні властивості.
1. Якщо деяка кодова комбінація належить циклічному коду, то комбінація отримана циклічною перестановкою вихідної комбінації (циклічним зсувом), також належить даному коду:
a1, a2 , , an 1, an ; an , a1, a2 , , an 1 .
2. Другою властивістю всіх дозволених комбінацій циклічних кодів є можливість їх ділення без залишку на деякий обраний поліном, називаний утворюючим. Синдромом помилки в цих кодах є наявність залишку від розподілу прийнятої кодової комбінації на утворюючий полін.
Ці властивості використовуються при побудові кодів, що кодують і декодує пристроїв, а також при виявленні і виправленні помилок.
Представлення кодової комбінації у вигляді багаточлена. Опис циклічних кодів і їхня побудова зручно проводити за допомогою багаточленів (або поліномів). У теорії циклічних кодів
кодові комбінації звичайно представляються у вигляді полінома. Так, n-елементну кодову комбінацію можна описати поліномом (n–1) ступеня, у вигляді:
|
A |
x a |
n 1 |
xn 1 |
a |
n 2 |
xn 2 a x a . |
(1) |
|
|
n 1 |
|
|
|
1 |
0 |
|
||
де ai 0,1 , причому ai 0 відповідають нульовим елементам комбінації, а ai 1 – ненульовим. |
|||||||||
Напишемо поліноми для конкретних 4-елементних комбінацій: |
|
|
|||||||
|
1101 A x x3 x2 1 |
, |
|
1010 A x x3 x . |
|
||||
|
1 |
|
|
|
|
|
2 |
|
|
Дії над багаточленами. При формуванні комбінацій циклічного коду часто використовують |
|||||||||
операції додавання багаточленів і розподілу одного багаточлена на іншій. Так, |
|
||||||||
A |
x A x x3 x2 1 x3 x x2 x 1 , |
оскільки x3 x3 |
1 1 x3 |
0 . |
|||||
1 |
2 |
|
|
|
|
|
|
|
|
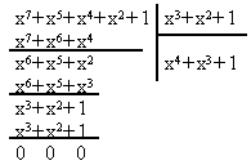
Слід зазначити, що дії над коефіцієнтами полінома (додавання та множення) виконуються по модулю 2. Розглянемо операцію розподілу на наступному прикладі (рис. 2).
Рис. 2. Виконання операції розподілу
Розподіл виконується, як звичайно, тільки віднімання заміняється підсумовуванням по модулю 2. Відзначимо, що запис кодової комбінації у вигляді багаточлена, не завжди визначає довжину кодової комбінації. Наприклад, при n 5, багаточлену x 1 відповідає кодова комбінація
00011.
Алгоритм одержання дозволеної кодової комбінації циклічного коду з комбінації простого коду. Нехай заданий поліном P x ar 1xr ar 2 xr 1 1 , що визначає коригувальну здатність
коду та число перевірочних розрядів r, а також вихідна комбінація простого k-елементного коду у |
|
вигляді багаточлена Ak 1 |
x . Потрібно визначити дозволену кодову комбінацію циклічного коду |
(n, k). |
|
1. |
Множимо багаточлен вихідної кодової комбінації на xr : |
|
|
|
A |
x xr . |
(2) |
|
k 1 |
|
|
2. |
Визначаємо перевірочні розряди, що доповнюють вихідну інформаційну комбінацію до |
||
дозволеної, як залишок від розподілу отриманого в попередньому пункті добутку на утворюючий поліном:
|
|
A |
x xr |
|
||
|
|
k 1 |
|
|
R(x) . |
(3) |
|
|
|
|
|
||
|
|
Pr (x) |
|
|||
3. Остаточно дозволена кодова комбінація циклічного коду визначиться так: |
|
|||||
A |
x A |
|
x xr R(x) . |
(4) |
||
n 1 |
|
k 1 |
|
|
|
|
Для виявлення помилок у прийнятій кодовій комбінації досить поділити її на утворюючий поліном. Якщо прийнята комбінація – дозволена, то залишок від ділення буде нульовим. Ненульовий залишок свідчить про те, що прийнята комбінація містить помилки. По виду залишку (синдрому) можна в деяких випадках також зробити висновок про характер помилки, її місці розташування та виправити помилку.
Формування базису (утворюючої матриці) циклічного коду. Формування базису циклічного коду можливо як мінімум двома шляхами.
Варіант перший.
1.Скласти одиничну матрицю для простого вихідного коду.
2.Визначити для кожної кодової комбінації вихідного коду групу перевірочних елементів і дописати їх у відповідні рядки матриці (рис. 3).
10000 xxxx
01000 xxxx
00100 xxxx
00010 xxxx
00001 xxxx
Рис. 3. Групи перевірочних елементів
Отримана матриця і буде базисом циклічного коду. Причому, у даному випадку, дозволені комбінації свідомо роздільні (тобто інформаційні та перевірочні елементи однозначно визначені).
Варіант другий.
1.Дописати ліворуч від КК, що відповідає утворюючому поліному циклічного коду нулі так, щоб довжина дозволеної кодової комбінації дорівнювала n.
2.Одержати інші дозволені кодові КК базису, використовуючи циклічний зсув вихідної. (У базисі повинне бути k – рядків)
У даному випадку код буде нероздільним.
Одержавши базис ЦК, можна одержати всі дозволені комбінації, проводячи додавання по модулю 2 кодових комбінацій базису в різних сполученнях і плюс НУЛЬОВА комбінація.
Циклічні коди досить прості в реалізації, володіють високою коригувальною здатністю (здатністю виправляти та виявляти помилки) і тому рекомендовані МСЕ-Т для застосування в апаратурі СПД. Відповідно до рекомендації V.41, у СПД з ОС рекомендується застосовувати код з
утворюючим поліномом P x x16 x12 x5 1 .
2. Кодування та декодування циклічного коду.
Побудова кодера циклічного коду. Розглянемо код (9,5) утворений поліномом:
|
|
|
|
P x x4 x 1 . |
|
|
(5) |
||
|
|
|
|
4 |
|
|
|
|
|
Дозволена комбінація циклічного коду F x утвориться з комбінації простого (вихідного) |
|||||||||
коду шляхом множення її на xr |
і додатка залишку |
R x |
від розподілу G(x)x r на утворюючий |
||||||
поліном Pr (x) . |
|
|
|
|
|
|
|
|
|
1. Множення полінома на одночлен |
xr еквівалентно додаванню до двійкової послідовності |
||||||||
відповідної |
G(x) , |
r |
– |
нулів |
праворуч. |
Нехай |
G(x) x4 x 1 10101. |
Тоді |
|
G(x)x4 x4 |
x2 1 x4 |
x8 x6 |
x4 101010000. |
Для |
реалізації операції додавання |
нулів |
|||
використовується r-розрядний регістр затримки.
2. Розглянемо більш докладно операцію ділення (рис. 4). Як бачимо з прикладу, процедура ділення одного двійкового числа на інше зводиться до послідовного додавання по модулю 2 дільники [10011] з відповідними членами діленого [10101], потім із двійковим числом, отриманим у результаті першого додавання, далі з результатом другого додавання і т. ін., поки число членів результуючого двійкового числа не стане менше числа членів дільника. Це двійкове число буде залишком R x .
Побудова формувача залишку циклічного коду. Структура пристрою, що здійснює розподіл на поліном цілком визначається виглядом цього полінома. Існують правила що дозволяють провести побудову формувача перевірочної групи (ФПГ) однозначно. Сформулюємо ці правила.
1.Число комірок пам’яті дорівнює ступеню утворюючого полінома r.
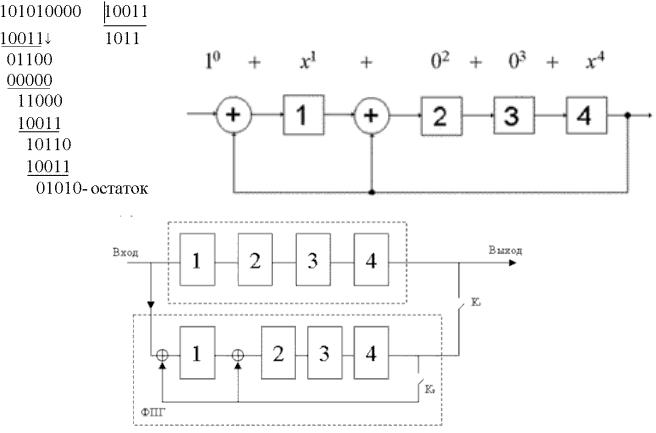
2.Число суматорів на одиницю менше ваги комбінації, що кодує, утворюючого полінома.
3.Місце установки суматорів визначається видом утворюючого полінома. Суматори ставлять після кожної комірки пам’яті, (починаючи з нульової), для якої існує ненульовий член полінома (рис. 5). Не ставлять після комірки, для якої у поліномі немає відповідного члена та після комірки старшого розряду.
4.У ланцюг зворотного зв’язку необхідно поставити ключ, що забезпечує правильний введення початкових елементів і вивід результатів ділення.
Рис. 4. Операція ділення |
Рис. 5. Розміщення суматорів |
Рис. 6. Структурна схема кодера ЦК (9,5)
Структурна схема кодера циклічного коду (9,5). Повна структурна схема кодера приведена на рис. 6. Вона містить регістр затримки та розглянутий вище ФПГ. Розглянемо роботу цієї схеми.
1.На першому етапі К1 – замкнутий, К2 – розімкнутий. Йде одночасне заповнення регістрів затримки та зсуву інформаційними елементами (старший уперед!) і через 4 такти старший розряд
вкомірці № 4.
2.Під час п’ятого такту К2 – замикається, а К1 – розмикається з цього моменту у ФПГ формується залишок. Одночасно з РЗ на вихід виштовхується затримка інформаційні розряди.
За 5 тактів (з 5 по 9 включно) у лінію підуть усі 5-інформаційних елемента. До цього часу у ФПГ сформується залишок
3.К2 – розмикається, К1 – замикається й у слід за інформаційними в лінію підуть елементи перевірочної групи.
4.Одночасно йде заповнення регістрів новою комбінацією.
Другий варіант побудови кодера ЦК. Розглянутий вище кодер дуже наочно відображає процес розподілу двійкових чисел. Однак, можна побудувати кодер з меншим числом елементів,
тобто більш економічний. Пристрій розподілу на утворюючий поліном P4 x x4 x 1 можна
реалізувати у вигляді згідно рис. 7. За п’ять тактів в комірках буде сформований такий же залишок від розподілу, що й у розглянутому вище формувачі перевірочної групи (ФПГ). За ці ж 5 тактів інформаційні розряди, видані відразу на модулятор. Далі, в слід за інформаційними розрядами ідуть перевірочні з комірок пристроїв розподілу. Однак, важливо відключити зворотний зв’язок на

момент виводу перевірених елементів, інакше вони спотворяться. Остаточно, структурна схема економічного кодера представлена на рис. 8. На першому такті Кл.1 і Кл.3 замкнуті, інформаційні елементи проходять на вихід кодера та одночасно формуються перевірочні елементи. Після того, як у лінію піде 5-ий інформаційний елемент, у пристрої розподілу сформуються перевірочні розряди. На 6-му такті ключі 1 і 3 розмикаються (розриваються зворотний зв’язок), а ключ 2 замикається, та в лінію ідуть перевірочні розряди. Комірки при цьому заповнюються нулями та схема повертається у початковий стан.
Рис. 7. Пристрій розподілу на виробляючий поліном P4 x x4 x 1
Рис. 8. Структурна схема економічного кодера циклічного коду (9,5)
Визначення помилкового розряду в ЦК. Нехай A x – багаточлен відповідний переданій КК. H x – багаточлен відповідний прийнятій КК. Тоді, сума даних багаточленів по модулю 2 дасть
багаточлен помилки: |
|
||||
E x A x H x . |
(5) |
||||
При однократній помилці, E x буде містити тільки |
один єдиний член відповідний |
||||
помилковому розряду. Залишок, що отриманий від ділення |
прийнятого багаточлена H x на |
||||
утворюючий Pr (x) дорівнює залишку, який отриманий при |
діленні відповідного багаточлена |
||||
помилок E x на Pr (x) : |
|
||||
|
H (x1) |
|
E(x1) |
. |
(7) |
|
|
|
|||
|
Pr (x) Pr (x) |
|
|||
При цьому, помилці в кожному розряді буде відповідати свій залишок R x (він же синдром). |
|||||
Як наслідок, одержавши синдром, можна однозначно визначити місце помилкового розряду. |
||||
Алгоритм визначення помилки. Нехай маємо n-елементні комбінації n k r , тоді: |
|
|||
1. Одержуємо залишок від ділення E x |
відповідного помилці в старшому |
розряді |
||
[1000000000], на утворюючий поліном Pr (x) : |
|
|
|
|
|
E1(x) |
R0 |
(x) . |
(8) |
|
Pr (x) |
|||
|
|
|
|
|
2.Ділемо отриманий поліном H x на Pr (x) і одержуємо поточний залишок R x .
3.Порівнюємо R0 x і R x . Якщо вони рівні, то помилка відбулася в старшому розряді.
Якщо «ні», то збільшуємо ступінь прийнятого полінома на х і знову проводимо ділення: |
|
||||
|
|
H (x) x |
R (x) . |
|
(9) |
|
|
|
|
||
|
|
Pr (x) |
0 |
|
|
|
|
|
|
|
|
4. |
Знову порівнюємо отриманий залишок с R0 x . Якщо вони рівні, то помилка в другому |
||||
розряді. |
Якщо ні, то множимо H (x) x2 і повторюємо ці операції доти, поки |
R x |
не буде |
||
дорівнювати R0 x . Помилка буде в розряді відповідному числу, на яке підвищена ступінь H x
плюс один. Наприклад: H (x) x3 R0 (x) , то номер помилкового розряду 3+1=4.
Pr (x)
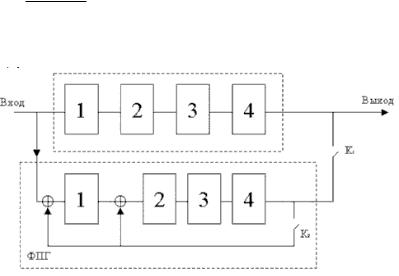
Декодер циклічного коду з виправленням помилки (рис. 9). Якщо помилка в першому розряді,
то залишок R0 (x) 10101 появляється після 9-го такту в комірках ФПГ.
Рис. 9. Декодер циклічного коду з виправленням помилки
Якщо в другому по старшинству, то після 10-го; у 3-му по старшинству – то після 11-го; у 4- му по старшинству – то після 12-го; у 5-му по старшинству – то після 13-го; у 6-му по старшинству
– то після 14-го; у 7-му по старшинству – то після 15-го; у 8-му по старшинству – то після 16-го; у 9-му по старшинству – то після 17. На 10-му такті старший розряд залишає регістр затримки та проходить через суматор по модулю 2. Якщо у цей момент залишок у ФПГ= R0 (x) , то логічна 1 з
виходу дешифратора надійде на другий вхід суматора та старший розряд інвертується. У нашому випадку інвертується другий розряд на 11-му такті.
3. Вибір утворюючого поліному.
Розглянемо питання вибору утворюючого полінома, що визначає коригувальні властивості циклічного коду. У теорії циклічних кодів показано, що утворюючий поліном являє собою добуток так званих мінімальних багаточленів mi (x) , що є простими співмножниками (тобто, що
ділиться без залишку лише на себе і на 1) бінома xn 1: |
|
P x m1(x) m3 (x) m j (x) , |
(10) |
де j d0 2 2tuош 1 2 2tuош 1. |
|
Існують спеціальні таблиці мінімальних багаточленів, одна з яких приведена нижче (табл. 1). |
|
Крім утворюючого полінома необхідно знайти і кількість перевірочних розрядів r. Вона
визначається з наступної властивості циклічних кодів: для |
будь-яких значень l і tuош існує |
||||||||||
циклічний код довжини n 2l 1, що виправляє всі помилки кратності |
tu |
ош |
і менш, і містить не |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
більш r l t |
|
перевірочних елементів. Так як l |
, то |
n 2 |
t |
uош |
1, відкіля: |
||||
uош |
|
|
|||||||||
tuош |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
r tuош log n 1 . |
|
|
|
|
|
|
(11) |
||
Очевидно, що для зменшення часу передачі КК, r варто вибирати як найменше. Нехай, |
|||||||||||
наприклад, довжина КК n 7 , кратність помилок, що виправляються tu |
ош |
1. З (11) одержимо |
|||||||||
r 1 log 7 1 3 . Після визначення кількості перевірочних розрядів r, |
|
|
|||||||||
обчислення утворюючого |
|||||||||||
полінома зручно здійснити користаючись табл. 1 мінімальних багаточленів.
Визначаючи утворюючий поліном, потрібно зі стовпця для відповідного співвідношення
|
r |
виписати всі багаточлени, |
|
починаючи з |
верхнього рядка до нижнього з номером |
||||||||||||
|
|
|
|||||||||||||||
|
tuош |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 2tuош 1 включно. Після цього, |
варто перемножити обрані мінімальні багаточлени відповідно |
|||||||||||||||
до (10). Так, якщо r 3 , |
tu |
ош |
1, j 2 1 1 1 , утворюючий поліном буде являти собою єдиний |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мінімальний |
багаточлен |
|
P x m (x) x3 x 1 |
(перший рядок, |
другий стовпець табл. 1). |
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Відповідно утворююче число дорівнює 1011. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 1 |
|
|
|
|
|
|
|
|
Мінімальні багаточлени для l |
r |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
tuош |
|
|
|
|||||||
|
j 2tuош 1 |
|
|
|
|
|
|
|
|
l |
|
|
|
||||
|
2 |
|
|
|
3 |
|
4 |
|
5 |
|
|
|
6 |
7 |
|
||
|
|
1 |
x2 x 1 |
|
x3 x 1 |
|
x4 x 1 |
|
x5 x 1 |
|
x6 x 1 |
x7 x 1 |
|
||||
|
|
3 |
– |
|
|
|
– |
|
x4 x3 |
|
x5 x4 x3 |
|
|
x6 x4 |
x7 x3 |
|
|
|
|
|
|
|
|
x2 x 1 |
|
x2 x 1 |
|
|
x2 x 1 |
x2 x 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5 |
– |
|
|
|
– |
|
– |
|
x5 x4 |
|
|
x6 x5 |
x7 x4 x3 |
|
|
|
|
|
|
|
|
|
x2 x 1 |
|
|
x2 x 1 |
x2 x 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
7 |
– |
|
|
|
– |
|
– |
|
– |
|
|
x6 x3 1 |
x7 x6 x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 x2 x 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Мажоритарне декодування блокових кодів. |
|
|
|
||||||||||||
Деякі блокові коди допускають реалізацію простого алгоритму декодування – алгоритму мажоритарного декодування (majority – більшість), що заснована на можливості виразити кожний інформаційний символ КК кількома способами через інші прийняті символи. Для ілюстрації цього алгоритму розглянемо систематичний код (7, 3) з утворюючою матрицею:
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
|
G |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
. |
(1) |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Даній матриці відповідають перевірочна та транспонована перевірочна матриці:
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
|
|
|
|||||||||||||
|
|
|
1 |
1 |
0 |
1 |
|
|
|||||||
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
||||
H |
(2), |
H T |
1 |
0 |
0 |
0 |
|
(3) |
|||||||
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
|
|
||||
|
|
|
0 |
0 |
1 |
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
Позначимо прийняту |
КК |
як |
|
F (х) (b1,b2 ,b3,b4 ,b5 ,b6 ,b7 ) . Оскільки |
розглянутий |
код є |
|||||||||
систематичний, перші 3 символи (b1, b2 , b3 ) є інформаційними. Використовуючи структурні
властивості цього коду, можна при декодуванні сформувати як тривіальні, так і складені оцінки інформаційних символів, які представлені в табл. 2. На основі стовпців перевірної матриці (3)
запишемо перевірочні співвідношення:
|
b1 b3 b4 |
0 , b1 b2 b3 b5 0 , b1 b2 b6 |
0 , |
b2 b3 b7 0 , |
(4) |
|||
які дозволяють сформувати складені оцінки. |
|
|
|
|
||||
|
|
|
|
|
|
|
Таблиця 2 |
|
|
|
Мажоритарне декодування блокового коду |
|
|
|
|||
|
|
|
Оцінки інформаційних символів |
|
|
|
|
|
|
Оцінки символу b1 |
|
Оцінки символу b2 |
|
Оцінки символу b3 |
|
|
|
|
|
|
Тривіальні оцінки |
|
|
|
|
|
|
b1 b1 |
|
b2 b2 |
|
|
b3 b3 |
|
|
|
|
|
Складені оцінки |
|
|
|
|
|
|
b1 b3 b4 |
|
b2 b4 b5 |
|
|
b3 b5 b6 |
|
|
|
b1 b5 b7 |
|
b2 b6 b7 |
|
|
b3 b7 b2 |
|
|
|
b1 b2 b6 |
|
b2 b3 b7 |
|
|
b3 b4 b1 |
|
|
Наприклад, на основі першої рівності з (4) маємо складену оцінку першого інформаційного символу b1 b3 b4 . Тривіальна оцінка цього символу і є, власне, цей символ b1 b1 , оскільки
код систематичний. Вирази для інших інформаційних символів складені аналогічно.
Після формування оцінок вони подаються на мажоритарний елемент, у якому рішення про кожний інформаційний символ виноситься «за більшістю голосів». Наприклад, якщо оцінки інформаційного символу b1 мають вигляд:
b1 b1 1, b1 b3 b4 1 , b1 b5 b7 1, b1 b2 b6 0 ,
серед яких кількість оцінок «1» перевищує кількість оцінок «0», то мажоритарний елемент виносить рішення «по більшості»: b1 1. Перераховані в табл. 2 складені оцінки називаються ортогональними перевірками, оскільки до них входять незбіжні символи. Число ортогональних
перевірок N і кратність помилок qвипр , що виправляються |
при мажоритарному декодуванні, |
перебувають у співвідношенні: |
|
qвипр (N 1) / 2 . |
(5) |
Код з утворюючою матрицею (2) дозволяє сформувати |
N 3 ортогональні перевірки та, |
відповідно, виправляти однократні помилки в інформаційних символах при значному спрощенні алгоритму декодування. Необхідно відзначити, що правила формування перевірок можуть мати циклічні властивості, що спрощує процедуру декодування.
Надалі розглянемо приклад: структура мажоритарного декодера систематичного коду (7, 3). Сформуємо структуру мажоритарного декодера коду (7, 3) на основі системи перевірок з табл. 1. Неважко побачити, що перевірки мають циклічні властивості. Наприклад, індекси в складених перевірках b1 b3 b4 , b2 b4 b5 , b3 b5 b6 змінюються на 1 убік зростання. З урахуванням
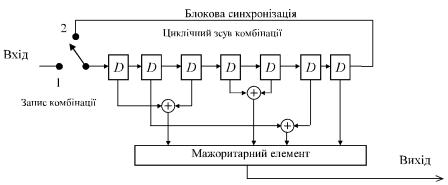
цього, структура декодера коду (7, 3), що реалізує мажоритарний алгоритм декодування, має вигляд, показаний на рис. 10.
Рис. 10. Структура мажоритарного декодера коду (7, 3)
Декодер складається з регістра зсуву, комутатора на вході, керованого системою блокової синхронізації, схем формування перевірок і мажоритарного елемента.
Декодер працює наступним чином. Спочатку комутатор на вході встановлюється в положення «1» і кодова комбінація, що декодується F (х) (b1,b2 ,b3,b4 ,b5 ,b6 ,b7 ) записується в комірки регістра зсуву. При цьому на входах мажоритарного елемента діють як тривіальні, так і складені перевірки, обумовлені табл. 2. Рішення про переданий інформаційний символ b1 зчитується з
виходу мажоритарного елемента. Потім комутатор установлюється в положення «2» і відбувається зсув комбінації на один символ. На цьому такті, у силу циклічних властивостей перевірок, формуються перевірки щодо другого інформаційного символу та рішення про інформаційний символ b2 зчитується з виходу мажоритарного елемента. Далі процес повторюється аж до
одержання на виході символу b3 .
5. Неалгебраїчні методи декодування циклічних кодів.
Всі методи декодування лінійних блокових кодів можна розділити на дві групи: алгебраїчні та неалгебраїчні. В основі алгебраїчних методів лежить рішення систем рівнянь, що задають значення і розташування помилок. Синдромні декодери відносяться саме до цієї групи методів. При неалгебраїчних методах та ж ціль досягається за допомогою простих структурних понять теорії кодування, що дозволяють знаходити комбінації помилок більш простим шляхом.
Прикладом неалгебраїчного методу є декодування з використанням алгоритму Мегіта, придатного для виправлення як одиночних, так і tu -кратних помилок (на практиці: tu 3 ). При
декодуванні відповідно до алгоритму Мегіта також обчислюється синдром S (x) прийнятої послідовності, однак використовується він інакше, ніж у розглянутих раніше синдромних декодерах. Ідея, що лежить в основі декодера Мегіта, дуже проста та ґрунтується на наступних властивостях ЦК:
- існує взаємно-однозначна відповідність між множиною всіх помилок, що виправляються,
та множиною синдромів; |
|
|
|
|
- якщо S (x) – синдромний |
багаточлен, |
що відповідає багаточлену |
помилок |
e( x) , то |
x S (x) modG(x) є синдромним багаточленом, що відповідає x e(x) mod(xn 1) . |
|
|||
Рівність a(x) b(x) mod p(x) |
читається як |
« a(x) , порівняно з b( x) за |
модулем |
p(x) » і |
означає, що a(x) і b( x) мають однакові залишки від ділення на поліном p(x) .
Таким чином, друга умова означає, що якщо комбінація помилок циклічно зсунута на одну позицію вправо, то для одержання нового синдрому потрібно зсунути зміст регістра зсуву зі зворотними зв’язками, що містить S (x) , також на одну позицію вправо.
Отже, основним елементом декодера Мегіта є регістр зсуву. Структурна схема декодера Мегіта для циклічних кодів довільної довжини приведена на рис. 11. Декодер працює наступним чином. Перед початком роботи зміст усіх розрядів регістрів дорівнює нулю. Прийнята послідовність r протягом перших n тактів вводиться в буферний регістр і одночасно з цим у ( n k )-розрядному регістрі зсуву зі зворотними зв’язками виконується її ділення на утворюючий поліном G(x) . Через n тактів у буферному регістрі виявляється прийняте слово r , а в регістрі
синдрому – залишок від ділення вектора помилки на утворюючий.
Обчислений синдром порівнюється з усіма табличними синдромами, і у випадку збігу з одним з них старший розряд буферного регістра виправляється шляхом додатка до його значення одиниці.
Після цього синдромний та буферний регістри один раз циклічно зсуваються. Це реалізує множення S (x) на x і ділення на G(x) . Зміст комірок синдромного регістра тепер дорівнює
залишку від ділення x S (x) на G(x) або синдрому помилки x e(x) mod(xn 1) . Якщо новий синдром збігається з одним з табличних, то виправляється чергова помилка і т. д. Через n тактів

усі позиції будуть, таким чином, виправлені. Розглянемо роботу декодера Мегіта для ЦК (7,4), що виправляє одиночну помилку. Схема декодера зображена на рис. 12. Принцип роботи декодера полягає в тому, що незалежно від того, в якій позиції відбулася помилка, здійснюється її зсув в останню комірку буферного регістра з відповідним перерахуванням синдрому та її виправлення в
цій позиції. Полином помилки в старшому розряді для коду Хемінга (7,4) має вигляд e6 (x) xn ,
якому відповідає синдромний поліном S6 (x) 1 x3 ( S (101) , детектор помилки налаштований на це значення синдрому. Нехай, наприклад, передана послідовність U 1001011, їй відповідає кодовий поліном U (x) 1 x3 x5 x6 . Відбулася помилка в третій позиції e(x) x3 , прийнятий
вектор має вигляд F 1000011, його поліном F (x) 1 x5 x6 . Коли прийнята послідовність цілком входить у буферний регістр, у регістрі синдрому виявляється синдром, що відповідає
помилці e(x) x3S (x) (110) . Оскільки він не збігається з табличним для e6 (x) xn , на виході детектора помилок буде нуль і виправлення не відбувається. Далі виконуються однократний циклічний зсув прийнятої послідовності в буферному регістрі, однократне ділення синдрому x S3
на утворюючий поліном у регістрі зі зворотними зв’язками та перевірка на збіг синдрому з заданим. Послідовність станів регістрів декодера в процесі декодування показана на рис. 13.
Рис. 11. |
Рис. 12. |
Рис. 13. Послідовність станів регістрів декодера в процесі декодування
Таким чином, виправлення помилки в декодері Мегіта здійснюється за 2n тактів: протягом п тактів виконується введення прийнятої послідовності в буферний регістр, протягом tu тактів –
виправлення помилки, і ще протягом n tu – відновлення буферного регістра у вихідний стан з
