
Завдання 1.
Первинна обробка вибірок. Варіаційні ряди. Вибіркові статистики. Надійні інтервали математичного сподівання, дисперсії, середньоквадратичного відхилення. Перевірка статистичних гіпотез
Фірма
має три торговельні точки, вибіркові
значення денних прибутків яких
представлені у вибірках
![]() (див. таблицю 1 додатків).
(див. таблицю 1 додатків).
-
Первинна обробка вибірок:
-
за вибірками
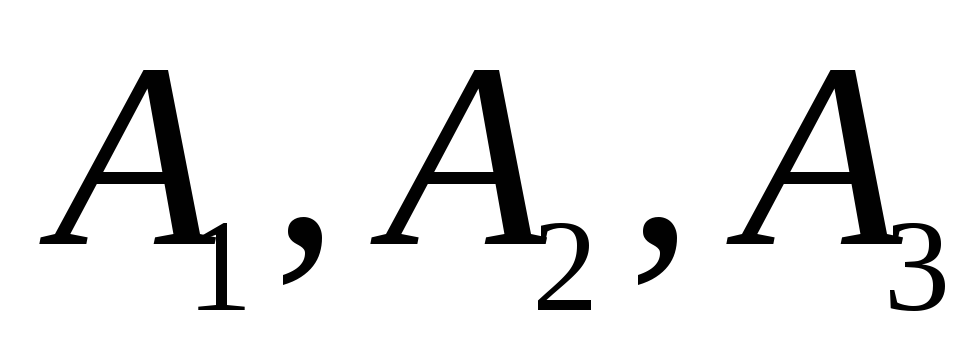 (
( -
вибірки з генеральних сукупностей
(ГС)
-
вибірки з генеральних сукупностей
(ГС)
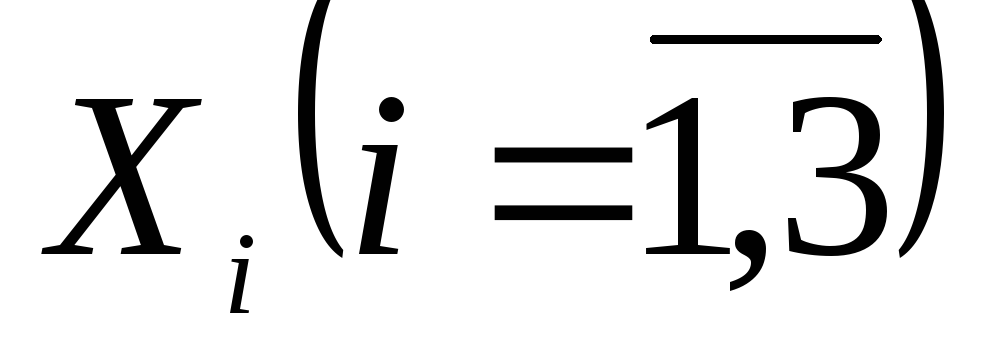 (
(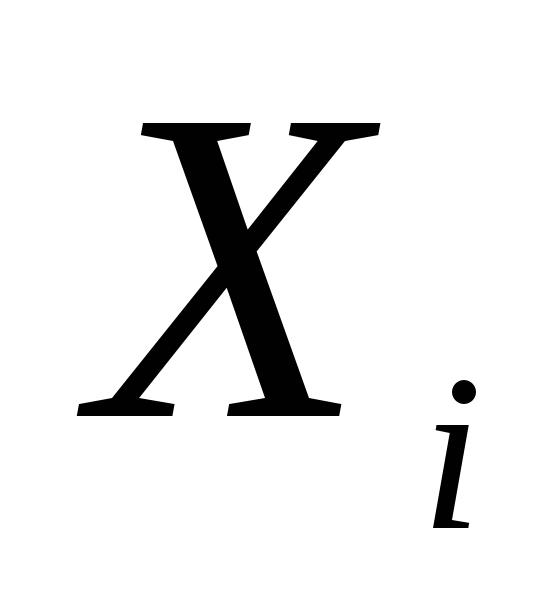 - прибуток по
- прибуток по
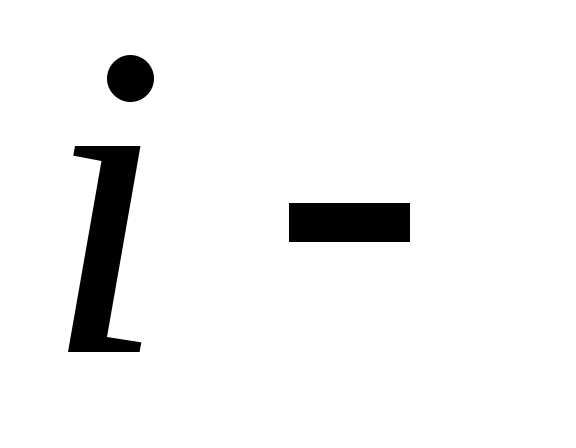 тому
магазину,
тому
магазину,
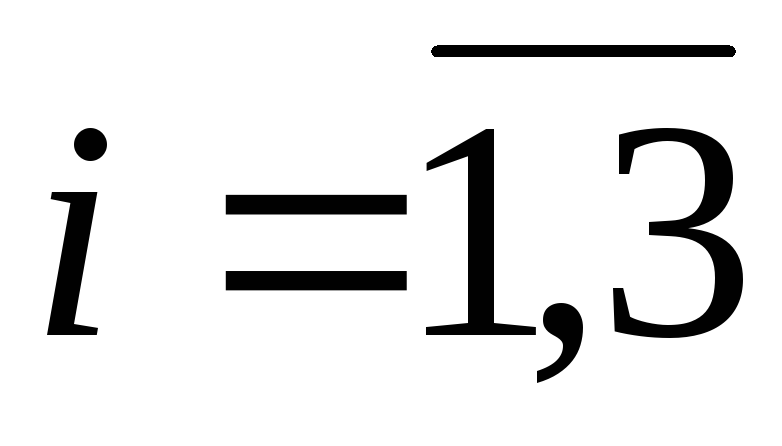 )
скласти дискретні варіаційні ряди
(ДВР);
)
скласти дискретні варіаційні ряди
(ДВР); -
за вибіркою
 ,
яка є об’єднанням вибірок
,
яка є об’єднанням вибірок
 і яка представляє собою вибірку з
генеральної сукупності
і яка представляє собою вибірку з
генеральної сукупності
 - прибуток по одному магазину фірми
(без урахування номеру), - інтервальний
варіаційний ряд (ІВР) із заданою
величиною інтервалу
- прибуток по одному магазину фірми
(без урахування номеру), - інтервальний
варіаційний ряд (ІВР) із заданою
величиною інтервалу
-
![]() ;
;
-
для вибірок
 обчислити відносні та накопичені
частоти;
обчислити відносні та накопичені
частоти;
-
побудувати полігон частот для
 та гістограму для
та гістограму для
 ;
; -
скласти емпіричну функцію розподілу для
 та побудувати графіки емпіричних
функцій розподілу для
та побудувати графіки емпіричних
функцій розподілу для
 .
.
-
Пошук вибіркових характеристик генеральних сукупностей
 по ДВР, складених за вибірками
по ДВР, складених за вибірками
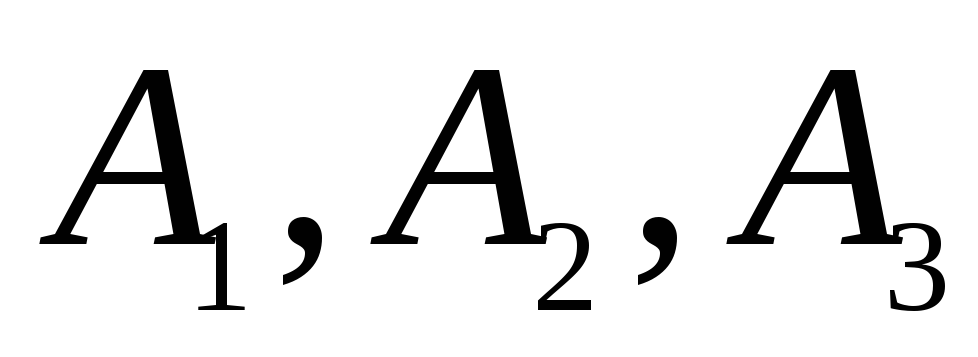 ,
по ІВР, складеному за вибіркою
,
по ІВР, складеному за вибіркою
 ,
знайти наступні вибіркові характеристики:
,
знайти наступні вибіркові характеристики:
-
вибіркове середнє арифметичне
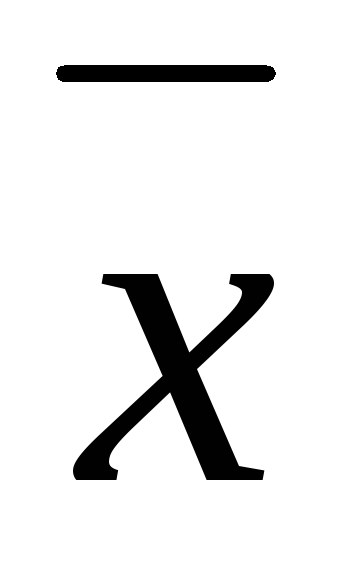 ;
; -
вибіркову дисперсію
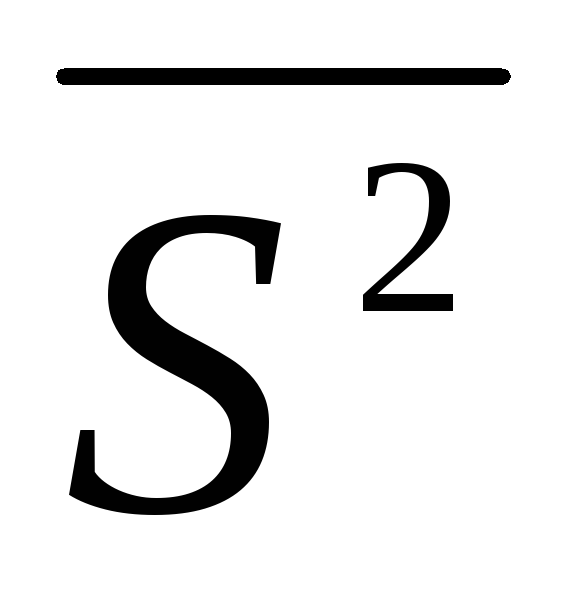 ;
; -
вибіркове середньоквадратичне відхилення
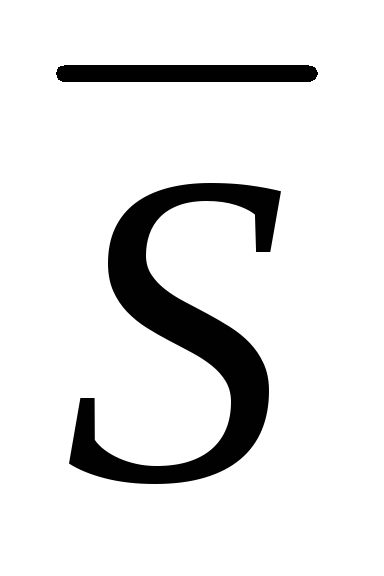 ;
; -
моду
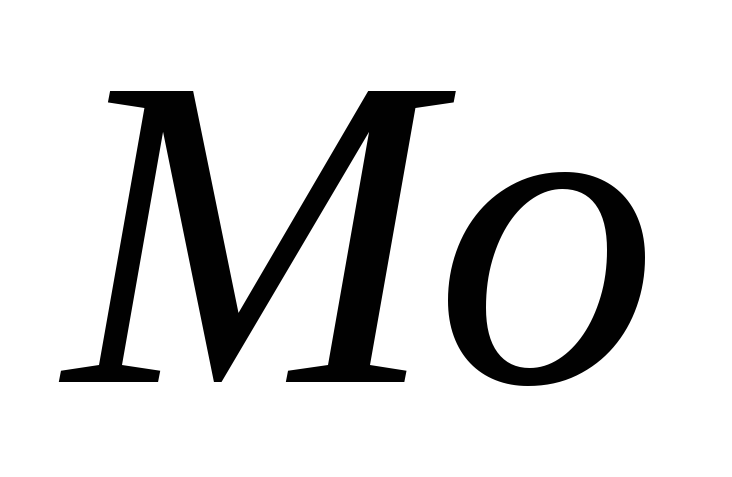 ;
; -
медіану
 .
.
-
Оцінки основних числових характеристик генеральних сукупностей
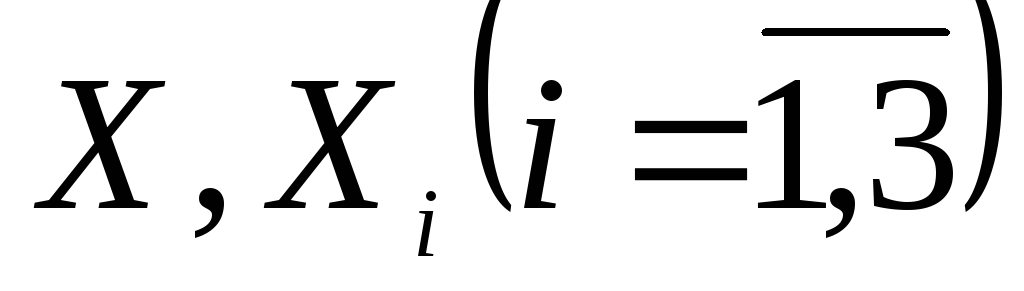 .
За вибірками
.
За вибірками
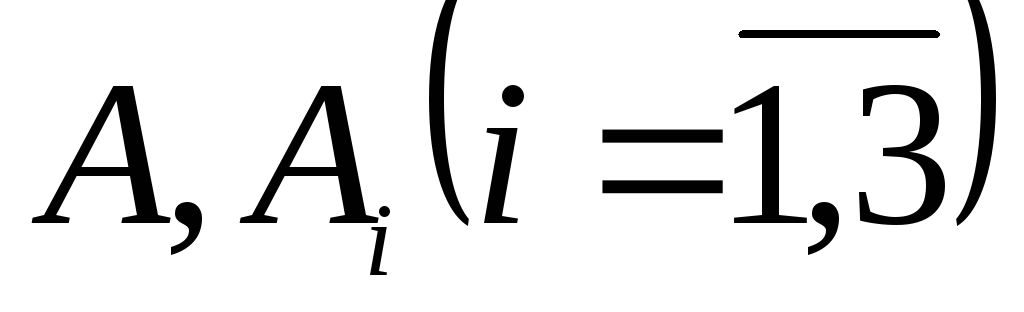 обчислити незсунені оцінки:
обчислити незсунені оцінки:-
математичного сподівання
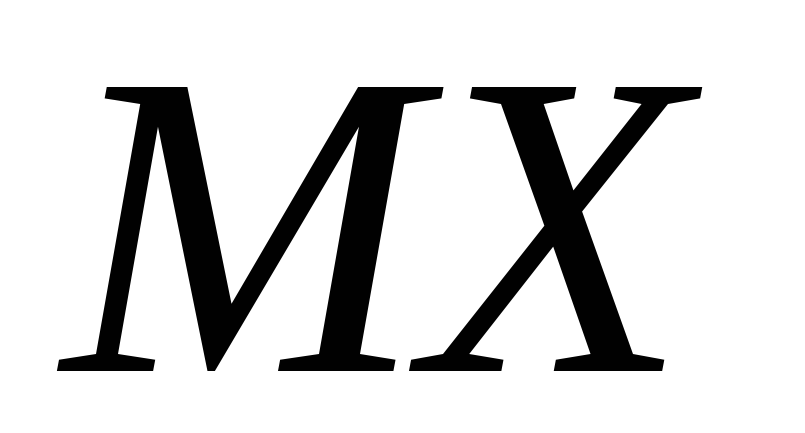 ;
; -
дисперсії
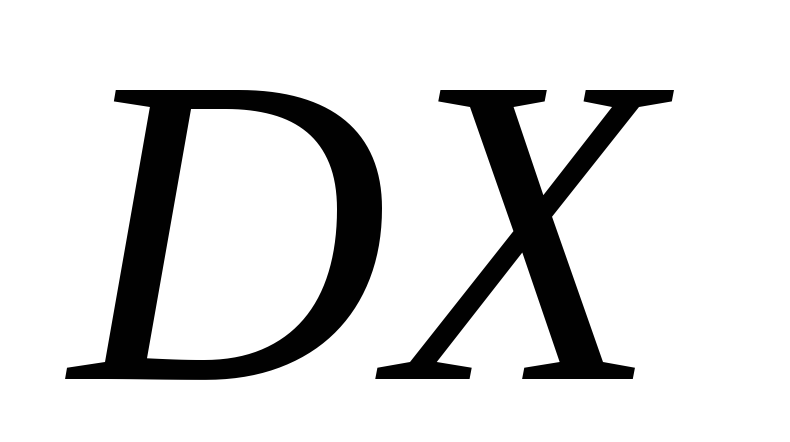 ;
; -
середньоквадратичного відхилення
 .
.
-
-
Інтервальні оцінки основних числових характеристик генеральних сукупностей
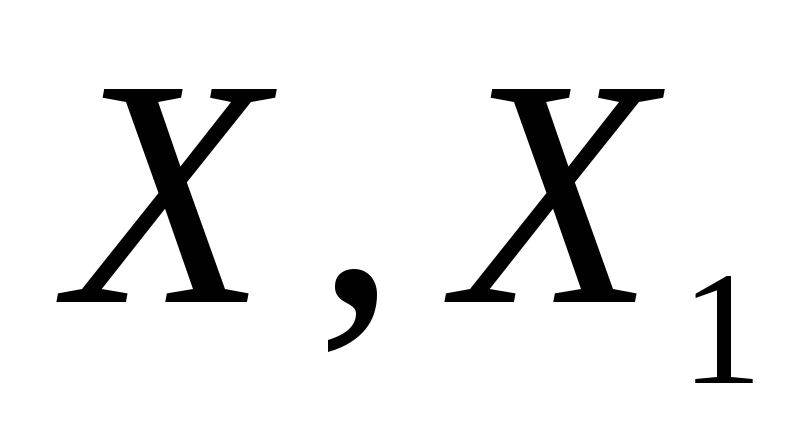 за вибірками
за вибірками
 .
Вважаючи генеральні сукупності нормально
розподіленими, з надійною ймовірністю
.
Вважаючи генеральні сукупності нормально
розподіленими, з надійною ймовірністю
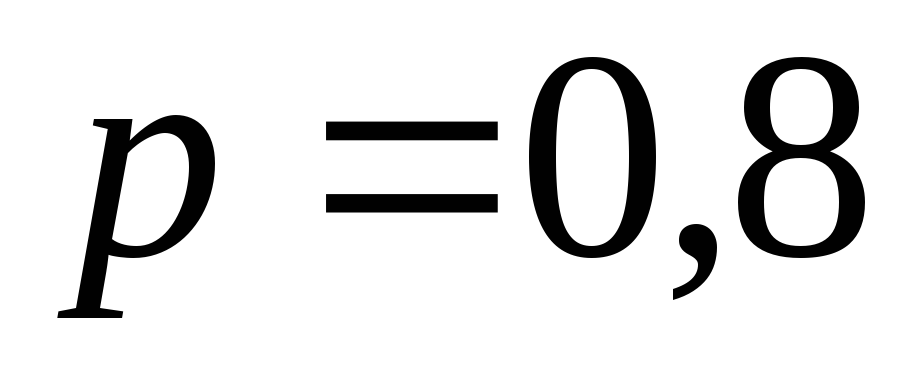 знайти надійні інтервали:
знайти надійні інтервали:-
Математичного сподівання :
-
-
при відомій дисперсії
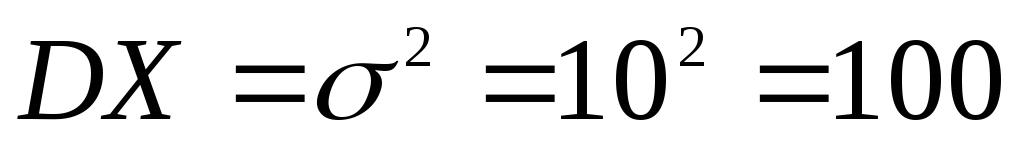 ;
; -
при невідомій дисперсії;
-
Дисперсії ;
-
Середньоквадратичного відхилення .
-
Мінімальний обсяг вибірки для пошуку надійного інтервалу математичного сподівання
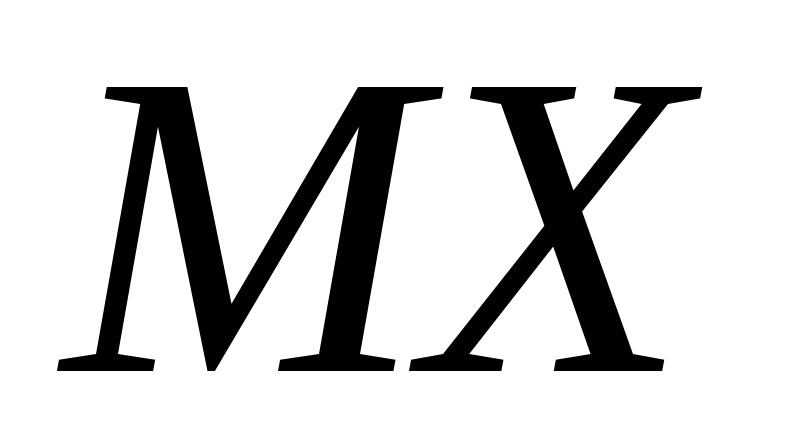 заданої наперед довжини. Вважаючи
генеральні сукупності
заданої наперед довжини. Вважаючи
генеральні сукупності
 нормально розподіленими, а вибірки
нормально розподіленими, а вибірки
 з генеральних сукупностей
з генеральних сукупностей
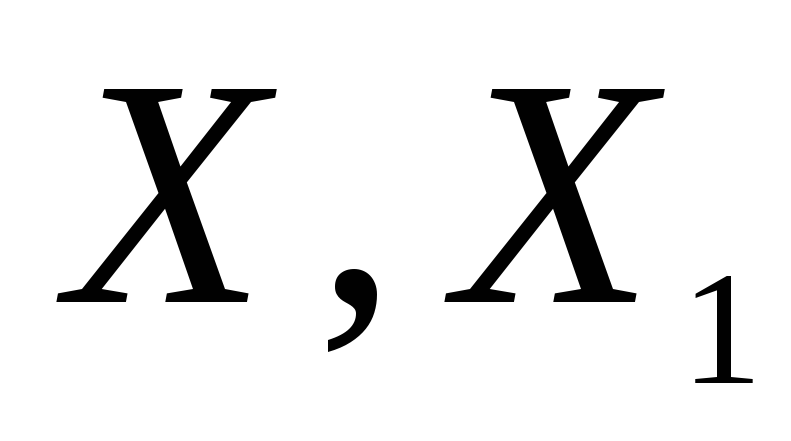 - пробними, з надійною ймовірністю
- пробними, з надійною ймовірністю
 визначити мінімальний об’єм вибірки
визначити мінімальний об’єм вибірки
 для пошуку надійного інтервалу
математичного сподівання
для пошуку надійного інтервалу
математичного сподівання
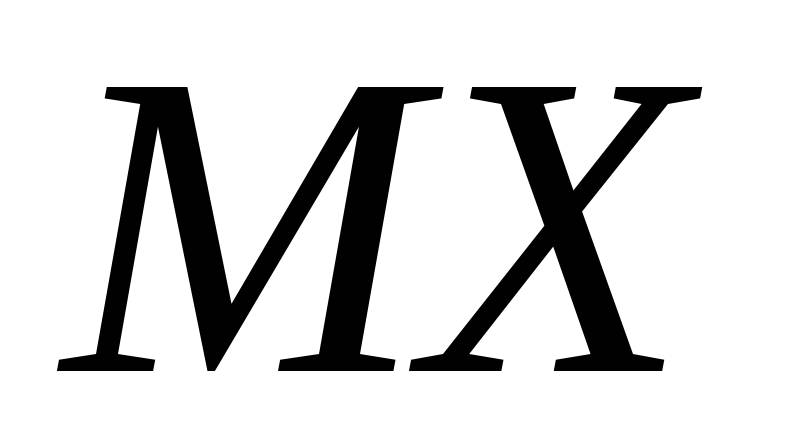 довжини
довжини
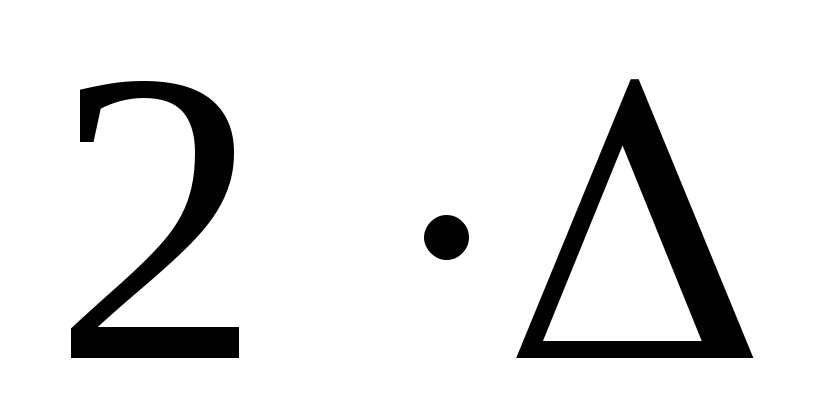 для
для
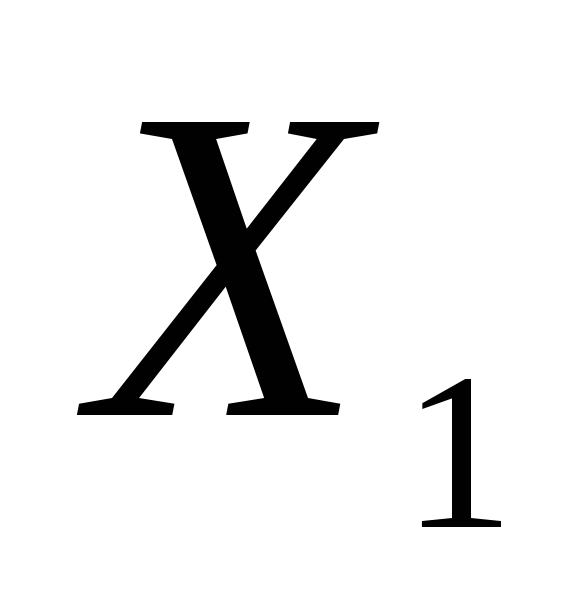 ;
довжини
;
довжини
 для
для
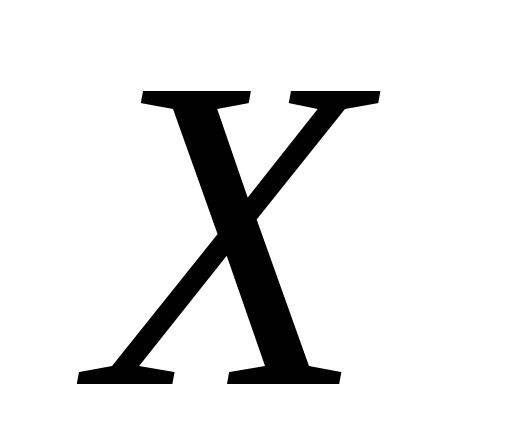 ,
якщо
,
якщо
![]() ,
,
-
відоме середньоквадратичне відхилення
 :
:
![]() ;
;
-
середньоквадратичне відхилення невідоме.
-
Перевірка статистичних гіпотез про параметри генеральних сукупностей
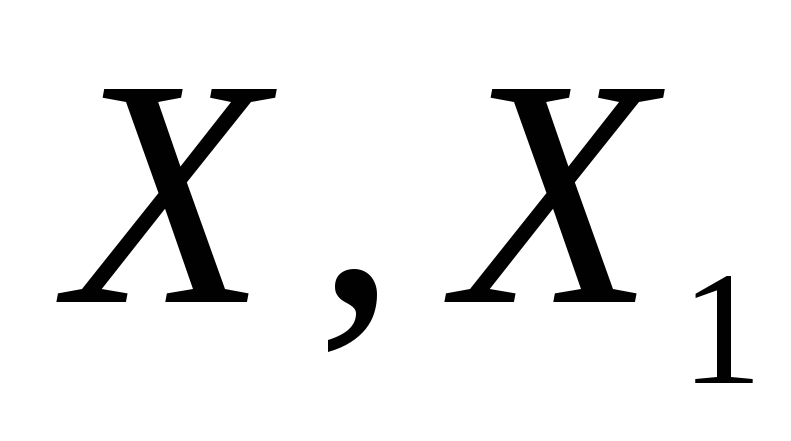 за вибірками
за вибірками
 .
Вважаючи генеральні сукупності
.
Вважаючи генеральні сукупності
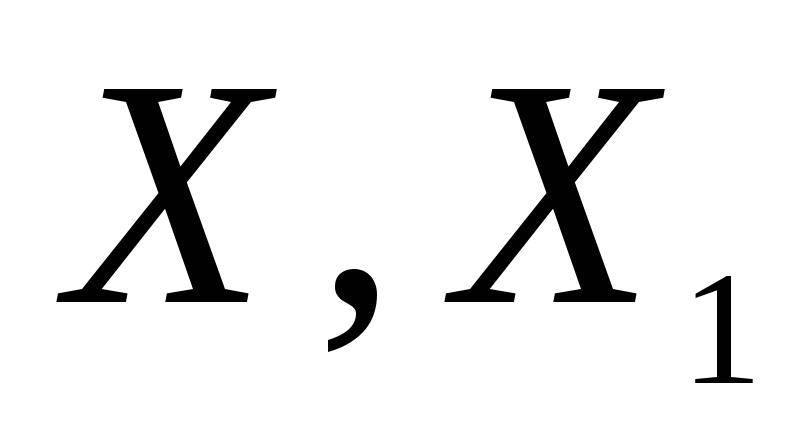 нормально розподіленими, за всіма
можливими альтернативними гіпотезами
перевірити нульові гіпотези:
нормально розподіленими, за всіма
можливими альтернативними гіпотезами
перевірити нульові гіпотези:-
за вибіркою
 при рівні значущості
при рівні значущості
 перевірити гіпотезу про рівність
дисперсії ГС
перевірити гіпотезу про рівність
дисперсії ГС
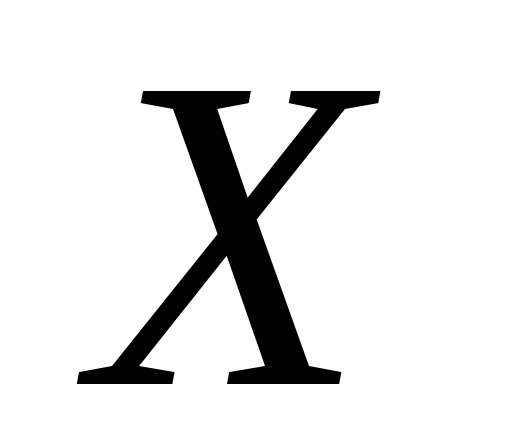 гіпотетичному значенню
гіпотетичному значенню
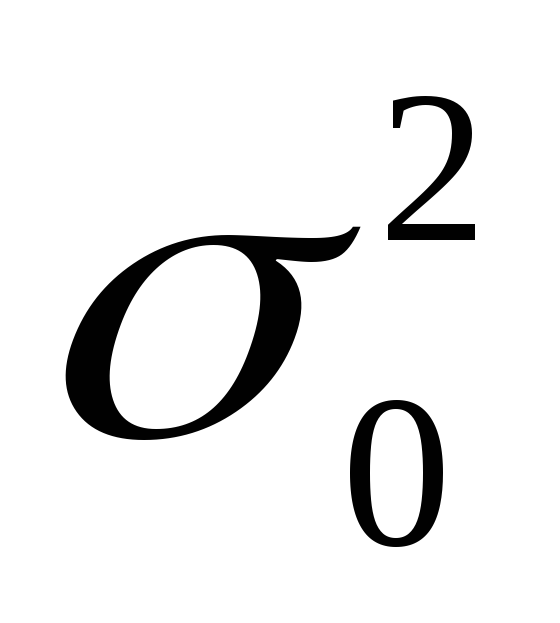 :
:
-
![]() ;
;
-
за вибіркою
 при рівні значущості
при рівні значущості
 перевірити гіпотезу про рівність
математичного сподівання ГС
перевірити гіпотезу про рівність
математичного сподівання ГС
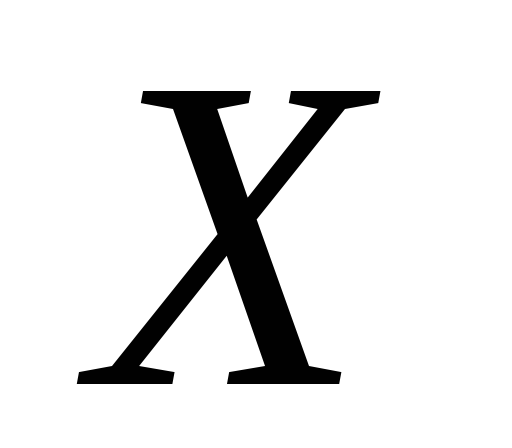 гіпотетичному значенню
гіпотетичному значенню
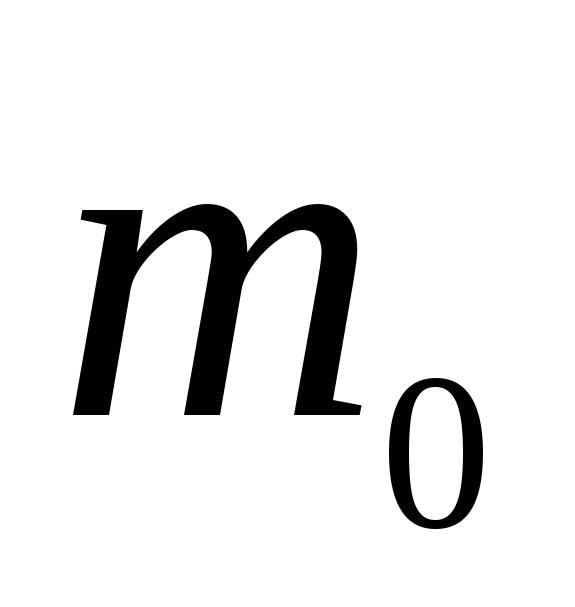 :
:
![]() ,
,
якщо
а) відоме
середньоквадратичне відхилення
![]() :
:
![]() ;
;
б) якщо середньоквадратичне відхилення невідоме;
6.3 за
вибірками
![]() при рівні значущості
при рівні значущості
![]() перевірити гіпотезу про рівність
математичних сподівань
перевірити гіпотезу про рівність
математичних сподівань
![]() ,
якщо відомо, що генеральні сукупності
,
якщо відомо, що генеральні сукупності
![]() незалежні, а вибірки
незалежні, а вибірки
![]() - достатньо великі,
- достатньо великі,
![]() ;
;
-
за вибірками
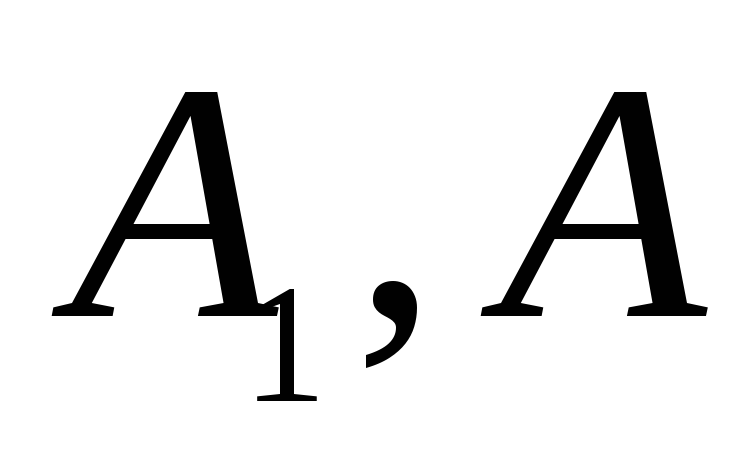 при рівні значущості
при рівні значущості
 :
:-
перевірити спочатку гіпотезу про рівність дисперсій
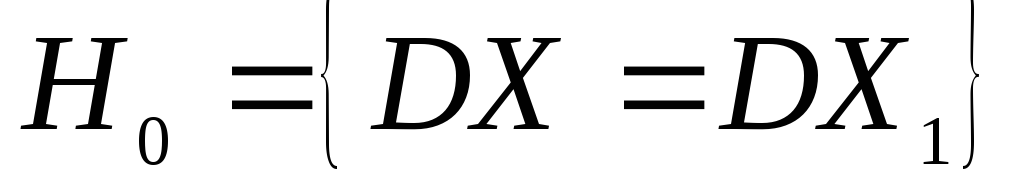 ;
; -
якщо
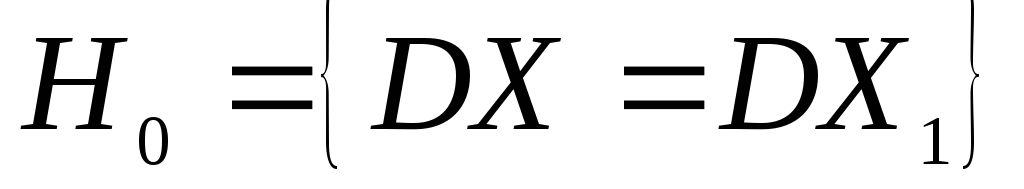 приймається перевірити також гіпотезу
про рівність математичних сподівань
приймається перевірити також гіпотезу
про рівність математичних сподівань
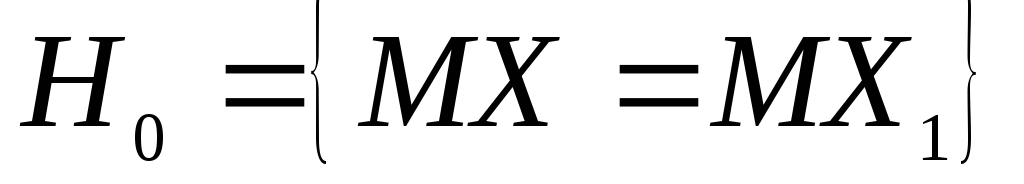 ,
якщо
,
якщо
-
![]() .
.
-
Перевірка статистичних гіпотез про розподіл генеральних сукупностей
 за вибірками
за вибірками
 .
За допомогою критерію згоди Пірсона
при рівні значущості
.
За допомогою критерію згоди Пірсона
при рівні значущості
 перевірити гіпотезу про нормальний
розподіл генеральних сукупностей
перевірити гіпотезу про нормальний
розподіл генеральних сукупностей
 ,
вважаючи всі параметри нормального
розподілу невідомими, якщо
,
вважаючи всі параметри нормального
розподілу невідомими, якщо
![]() .
.
-
Факторний аналіз (однакова кількість спостережень на кожному рівні фактора). Розглянути наступний фактор – розподіл на окремі магазини. За вибіркою
 при рівні значущості
при рівні значущості
 перевірити гіпотезу про рівність
середніх прибутків за всіма магазинами.
З цією метою:
перевірити гіпотезу про рівність
середніх прибутків за всіма магазинами.
З цією метою:-
перевірити гіпотезу про рівність дисперсій на всіх рівнях фактора:
 .
Якщо вона не приймається, виокремити
рівень фактору з відмінною від інших
дисперсією і повторити процедуру;
.
Якщо вона не приймається, виокремити
рівень фактору з відмінною від інших
дисперсією і повторити процедуру; -
для факторів, стосовно яких підтвердилася гіпотеза про рівність дисперсій, перевірити гіпотезу про рівність математичних сподівань, якщо
-
![]() .
.
9. Економічна інтерпретація результатів та розробка рекомендацій. Порівняти очікувані прибутки та стабільність роботи кожного магазину та фірми в цілому, зробити висновки та виробити рекомендації про шляхи вдосконалення діяльності фірми загалом та окремих її магазинів.
Розв’язання
Введемо
наступні позначення для завдань, хід
розв’язання яких наводиться в даному
пункті:
![]() - номер завдання,
- номер завдання,
![]() .
У цих позначеннях
.
У цих позначеннях
-
1.3
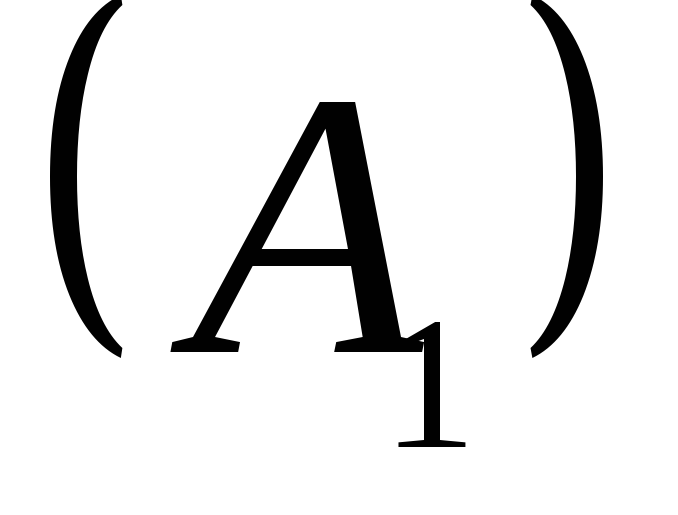 означатиме, що завдання 1.3 виконується
для генеральної сукупності
означатиме, що завдання 1.3 виконується
для генеральної сукупності
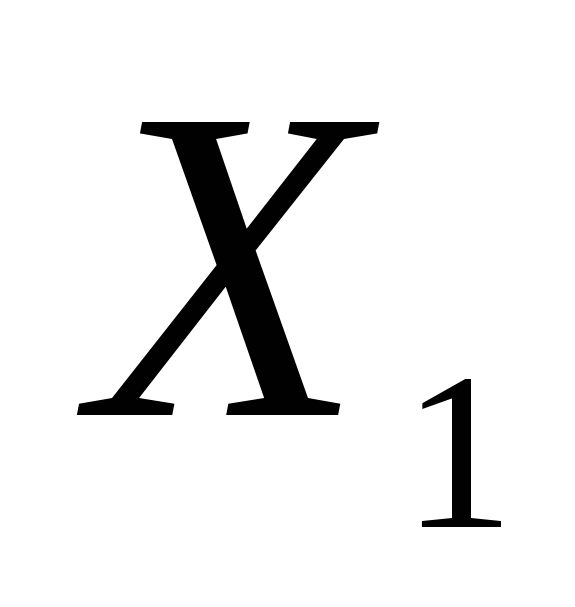 за вибіркою
за вибіркою
 ;
; -
1.2 означатиме, що виконується саме це завдання.
