5.2 Критерій Найквіста

Замкнена система стійка, якщо розімкнена система стійка і її АФХ не охоплює критичну точку, тобто координати (–1;j0). Оскільки в нашому випадку система має запізнювальну ланку, то наявність запізнення не впливає на стійкість розімкненої системи. В такому випадку ми будемо розглядати ПФ розімкненої системи без запізнення, тобто ПФ вигляду:

Для побудови АФХ необхідно виділити дійсну та уявну частину даної функції, тобто звести її до вигляду

Ураховуючи, що , а відповідно. Підставляючи всі зроблені перетворення у нашу ПФ, будемо мати:

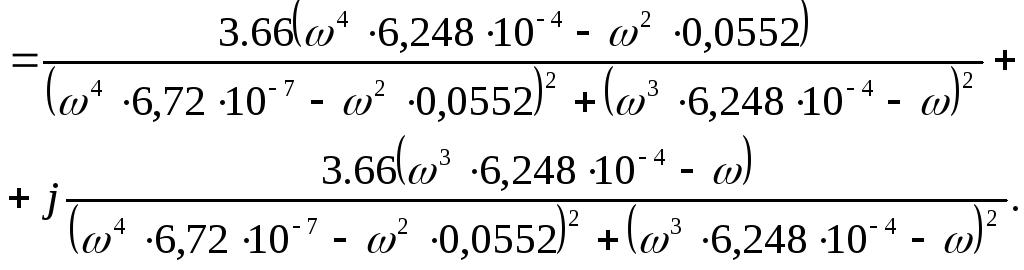
Побудуємо годограф за допомогою MathCAD2001:

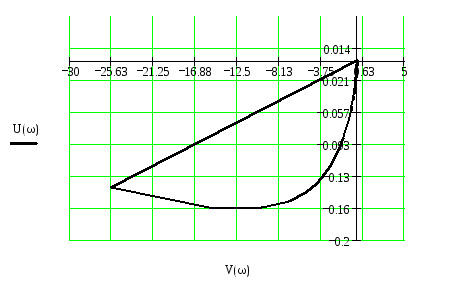
Рис. 2. Годограф неперервної частини розімкненої системи

Як бачимо, годограф побудованої ПФ не охоплює точку (-1;j0).

Висновок: система стійка за критерієм Найквіста.

Побудуємо ЛАЧХ та ЛФЧХ і графічно визначимо запас стійкості за фазою та по амплітудою.

Як бачимо з графіків, які подані на рис. 3 і 4, запас за амплітудою: і за фазою

Висновок: система коригування не потребує.

Будуємо ЛАЧХ і ЛФЧХ за допомогою Matlab 2000:

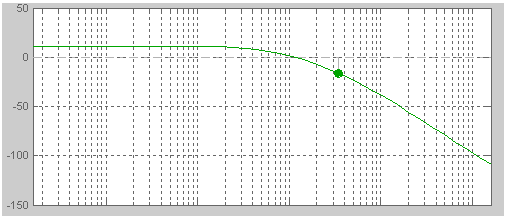
Рис. 3. ЛАЧХ розімкненої системи

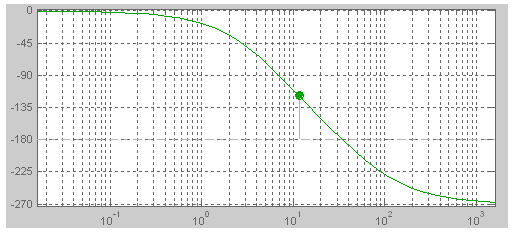
Рис. 4. ЛФЧХ розімкненої системи

6 Перехідний процес системи

Визначимо закон зміни вихідної величини замкненої системи при ступінчастій задаючій функціїі нульових початкових умовах.

ПФ замкненої системи буде:

Визначимо корені знаменника. Для цього використаємо програму MathCAD2000.

Отже,

Оскільки р – оператор, то для переходу до оригіналу скористуємося теоремою розгортки:

де - чисельник ПФ розімкненої системи;

- знаменник ПФ розімкненої системи.

Тоді оригінал може бути знайдений як

Далі, виконуючи відповідні розрахунки, отримаємо функцію перехідного процесу в нашій системі.

За допомогою програми MathCAD2001 побудуємо графік перехідного процесу:

Рис. 5. Перехідний процес системи

7 Визначення якісних показників перехідного процесу

Оцінимо різницю між максимальним значенням перехідної характеристики та її встановленим значенням, тобто визначимо пере регулювання.

Допущене значення відхилення вибираємо , тоді час регулювання.

8 Швидкісна похибка слідкуючої системи

У слідкуючи системах з астатизмом першого порядку швидкісна похибка з’являється з постійною швидкістю. Максимальна швидкість обертання об’єкта керування .

Тоді швидкісна похибка буде дорівнювати:

9 Інструментальна похибка слідкуючої системи

Інструментальна похибка слідкуючої системи зумовлена нелінійностями статичних характеристик її функціональних елементів. Основними джерелами її появи в цифроаналоговій системі є: потенціометр зворотного зв’язку, АЦП і знижувальний редуктор.

Максимальна інструментальна похибка:

Середньоквадратична інструментальна похибка:

Література:

1. Попович М.Г.,Ковальчук О.В. Теорія автоматичного керування:Підручник.-К.:Либідь,2007.-656с.

2. Галай М.В. Теорія автоматичного керування.:неперервні та дискретні системи.:навчальний посібник.-Полтава;ПНТУ,2005-454с.

3. Галай М.В.Импульсні,цифрові та релейні системи.

4. Галай В.М. Теорія цифрових систем автоматичного керування.:Навчальний посібник.-Полтава:ПНТУ,2009.-131с.