4 Передавальна функція системи

Визначимо передавальну функцію системи.

Для розімкненого каналу (системи):

де – передавальна ланка обчислювального пристрою =

–передавальна функція (ПФ) ЦАП;

–ПФ підсилювача потужності;

–ПФ ДПС;

–ПФ знижувального редуктора;

–ПФ дротяного потенціометра;

- ПФ АЦП.

Підставивши всі визначені передавальні функції в одну, будемо мати:

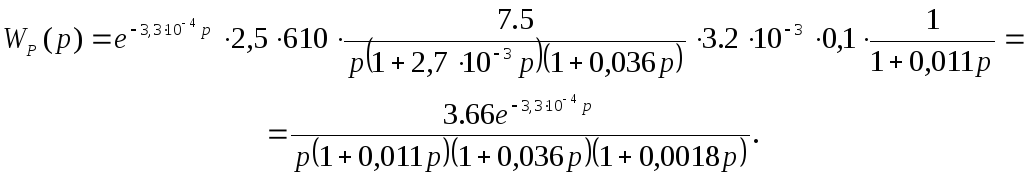
Для замкнутої системи:

,

Для замкнутої системи відносно похибки:

.

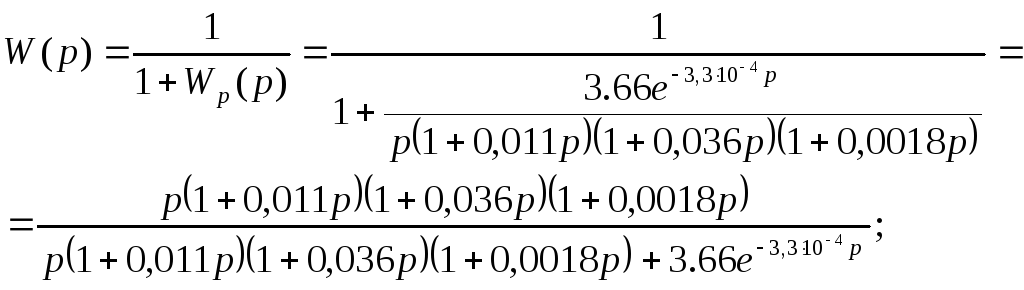Для того, щоб виконати z-перетворення кожної з передавальних функцій системи, необхідно розкласти кожну функцію на прості дроби. Оскільки система має у своєму складі запізнювальну ланку, а саме її ПФ , то при розкладанні такої функції у степеневий ряд можна отримати нескінченне число коренів, які в свою чергу будуть прямувати до нуля. Тому достатньо обмежитися максимальним показником ступеня нашої передавальної – 4. Отже, для здійснення z – перетворення для ПФ замкненої системи беремо функцію виду:

Приведемо дану ПФ до суми простих дробів у вигляді:

Переходячи від доі приводячи наше рівняння до спільного знаменника, будемо мати:

Далі розкриваємо дужки і зводимо все до полінома четвертого ступеня виду

Звідки складаємо систему рівнянь:

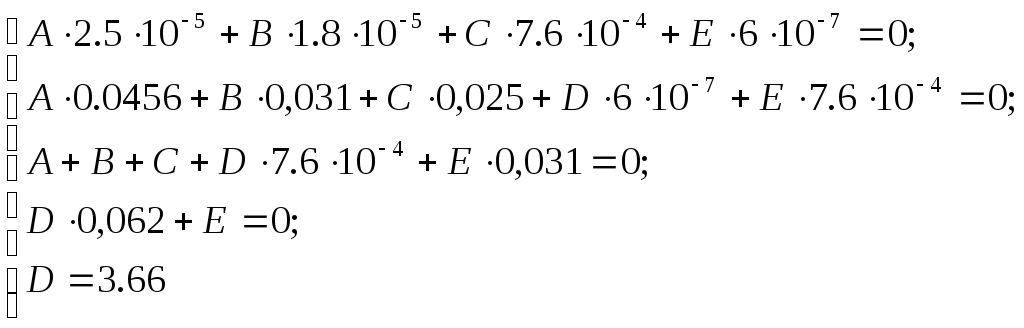
Розв’язуючи цю систему рівнянь за допомогою програми MathCAD2001, отримуємо відповідь:

Тоді

Дискретна ПФ розімкненої системи із запізненням визначається наступною формулою:

.

Використавши таблицю z - перетворень отримаємо:

(Для прикладу розглянемо перетворення функції . Із таблиці z – перетворення знаходимо, що при загальному виглядіУ нашому випадку, Т – період дискретизації = 0,00244 (визначеновище). Тоді отримаємо наступну z – перетворену функцію:і т.д.)

Спростивши вираз (приводячи все до спільного знаменника), отримаємо:

Визначимо дискретну передавальну функцію замкненої системи:

.

Для цього нам спочатку потрібно знайти ПФ неперервної частини, тобто привести її до можливості z – перетворення.

Використовуючи метод невизначених коефіцієнтів, перетворимо дану ПФ до суми простих дробів:

Приведемо до спільного знаменника:

Далі розкриваємо дужки і зводимо все до полінома третього ступеня виду

Звідки складаємо систему рівнянь:

Розв’язуючи цю систему рівнянь за допомогою програми MathCAD2001, отримуємо відповідь:

Тоді, підставляючи всі отримані дані, будемо мати:

Дискретна передавальна функція замкненої системи із запізненням визначається також за допомогою таблиці z – перетворень:

Визначимо дискретну ПФ ЗЗ:

ПФ неперервної функції:

Виконаємо z – перетворення:

Тоді дискретна ПФ замкненої системи визначиться так:

5 Визначення стійкості системи

5.1 Критерій Гурвіца

ПФ замкненої системи має вигляд:

Система стійка, якщо діагональний визначник Гурвіца та його мінори більші 0. Визначник Гурвіца складають із коефіцієнтів характеристичного рівняння замкненої системи.

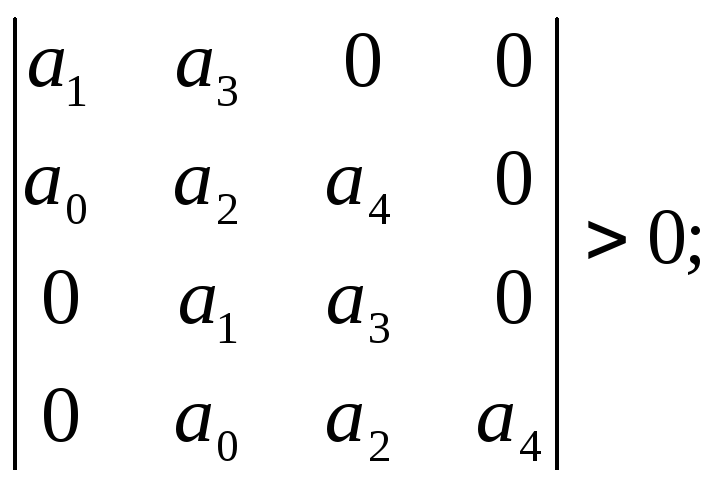У нашому випадку знаменник ПФ замкненої системи містить член запізнювальної ланки . Тому з достатньою точністю можна розкласти числоустепеневий ряд. Візьмемо три перших члени ряду:

Тоді, враховуючи таку підстановку, отримаємо поліном знаменника вигляду:

Тут

і т.д.

Висновок: система стійка за критерієм Гурвіца.