4.2. Построение функции полезности

Однако уверены ли мы в том, что вообще существует какой-либо способ приписывания товарным наборам порядковых полезностей? Допустим, имеется некое ранжирование предпочтений. Всегда ли можно найти функцию полезности, располагающую товарные наборы в том же порядке, в каком располагаются эти предпочтения? Существует ли функция полезности, описывающая любое рациональное ранжирование предпочтений?

Не все виды предпочтений можно представить с помощью функции полезности. Предположим, например, что предпочтения некоего индивида нетранзитивны, так что A  B  C  A. Тогда функция полезности, соответствующая этим предпочтениям, должна была бы состоять из чисел u(A), u(B) и u(C) таких, что u(A) > u(B) > u(C) > u(A). Но это невозможно.

Если, однако, исключить из рассмотрения аномальные случаи вроде нетранзитивных предпочтений, то окажется, что практически всегда можно найти некую функцию полезности, которая бы представляла данные предпочтения. Поясним построение функции полезности наглядными примерами, рассмотрев один из них здесь, а другой — в гл. 14.

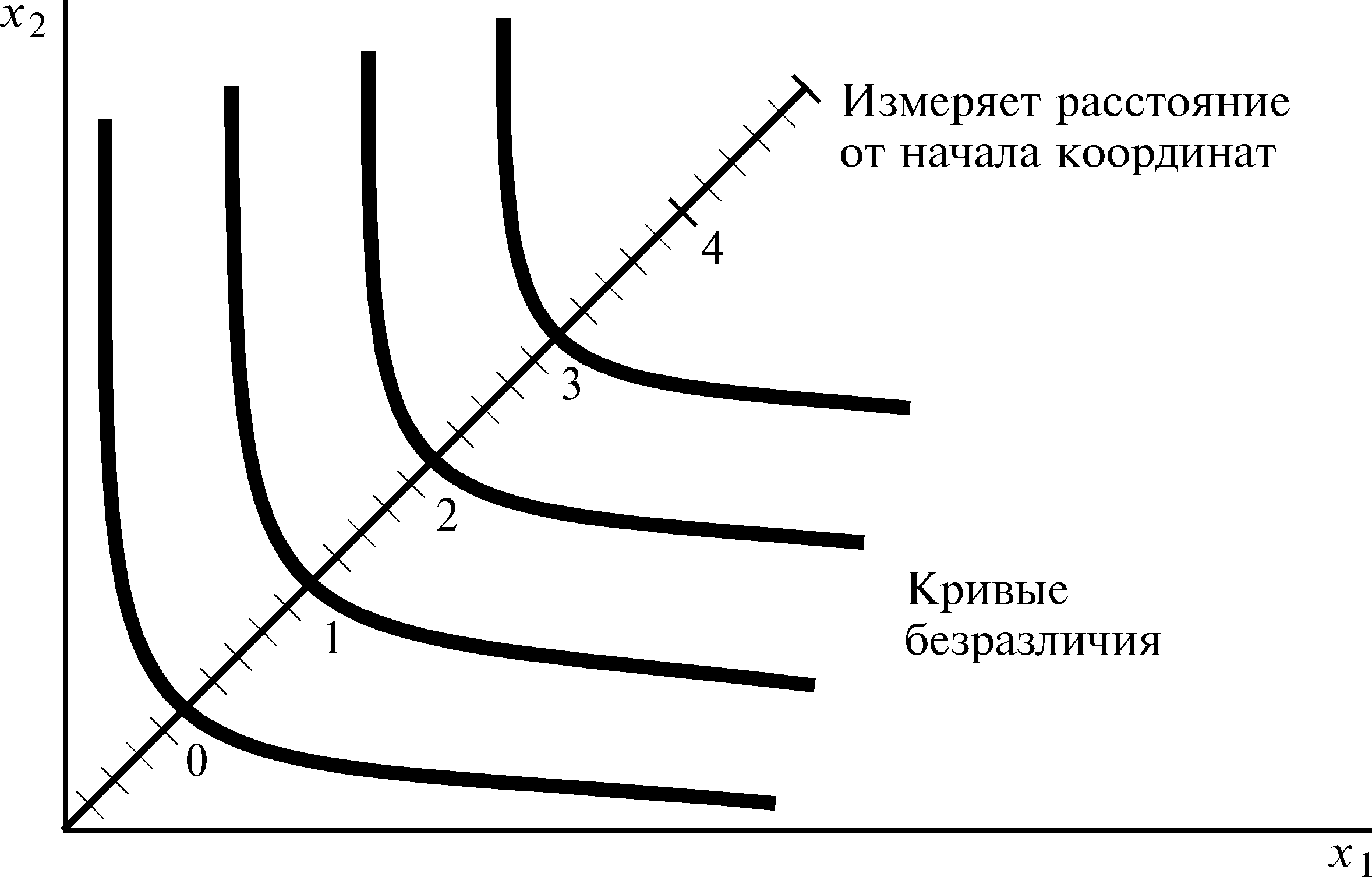
Допустим, что нам дана карта кривых безразличия, такая, как на рис. 4.2. Мы знаем, что функция полезности есть способ обозначения кривых безразличия, при котором более высоким кривым безразличия ставятся в соответствие бóльшие числа. Как это можно сделать?

Рис. 4.2

Построение функции полезности на основе кривых безразличия. Нарисуйте диагональную линию и обозначьте каждую кривую безразличия числом, соответствующим расстоянию от нее до начала координат, измеренному вдоль этой линии.

Один из простых способов — провести диагональ, как показано на рисунке, и обозначить каждую кривую безразличия числом, соответствующим ее расстоянию от начала координат, измеренному вдоль этой диагонали.

Откуда мы знаем, что в результате этого получим функцию полезности? Нетрудно заметить, что если предпочтения монотонны, то луч, проходящий через начало координат, должен пересечь каждую кривую безразличия в точности один раз. Таким образом, каждый набор благ получает свое обозначение, и наборы, находящиеся на более высоких кривых безразличия, обозначаются бóльшими числами, а только это и требуется, чтобы построить функцию полезности.

Это дает нам один из способов обозначения кривых безразличия по крайней мере для случая монотонных предпочтений. Данный способ не всегда будет самым подходящим для любого заданного случая, но он показывает достаточно общий характер идеи, заложенной в функции порядковой полезности: "разумные" предпочтения почти любого вида можно представить с помощью функции полезности.

4.3. Некоторые примеры функций полезности

В гл. 3 мы рассмотрели несколько примеров предпочтений и представляющих их кривых безразличия. Эти предпочтения можно представить также с помощью функций полезности. Если дана функция полезности u(x₁, x₂), нарисовать соответствующие кривые безразличия сравнительно несложно: надо нанести на график все точки (x₁, x₂), для которых u(x₁, x₂) постоянна. В математике множество всех (x₁, x₂), для которых u(x₁, x₂) постоянна, называется упорядоченным множеством. Для каждого другого значения константы мы получаем другую кривую безразличия.

ПРИМЕР: Кривые безразличия, получаемые на основе функции полезности

Предположим, что функция полезности имеет вид: u(x₁, x₂) = x₁x₂. Как выглядят тогда кривые безразличия? Нам известно, что типичная кривая безразличия есть просто множество всех x₁ и x₂, таких, что k = x₁x₂ для некой константы k. Выразив x₂ как функцию от x₁, мы видим, что типичной кривой безразличия в данном случае будет соответствовать формула:

Эта кривая изображена на рис. 4.3 для k = 1, 2, 3...

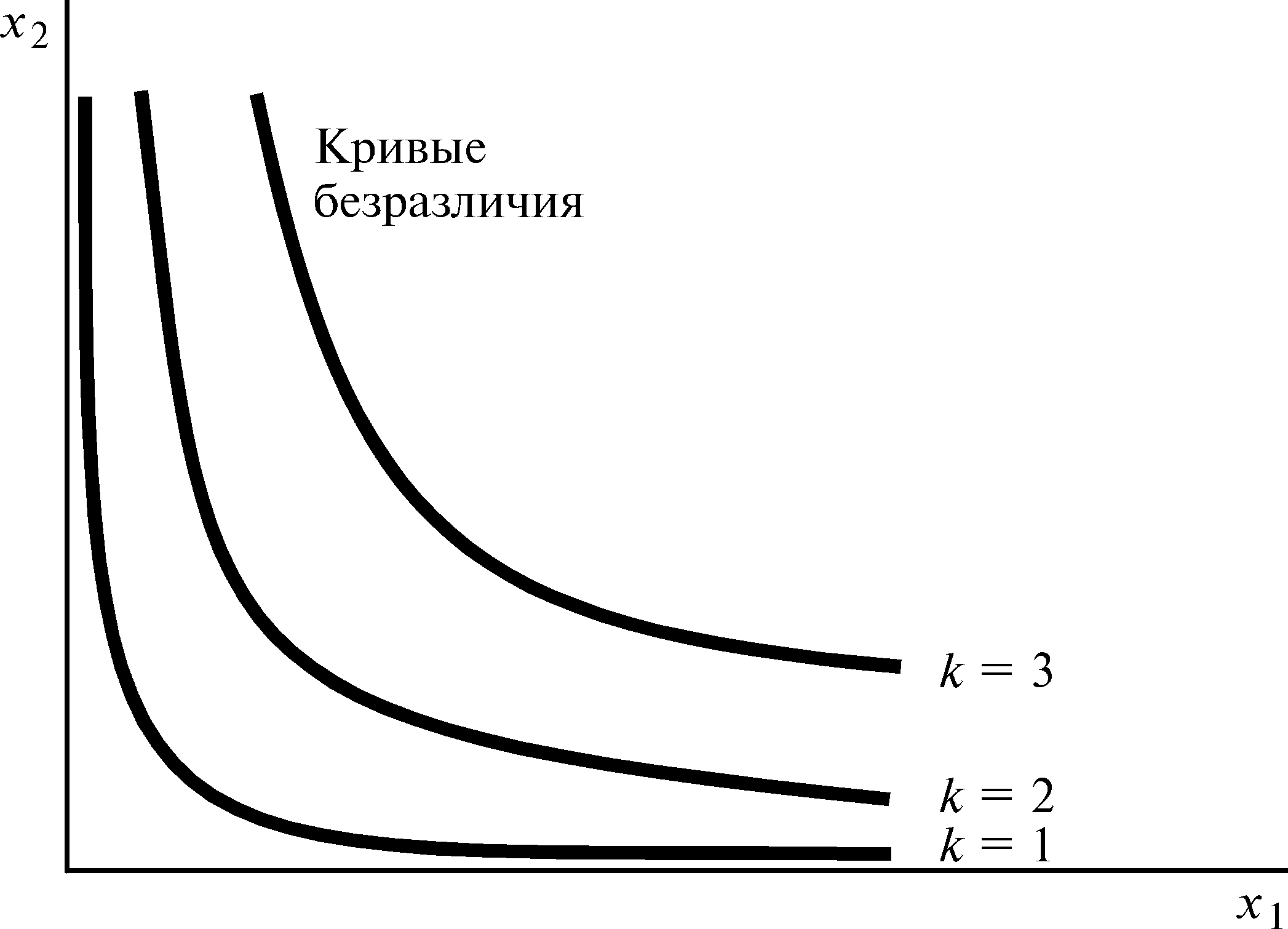
Кривые безразличия. Кривые безразличия k = x1x2 для любых значений k.

Рис. 4.3

Рассмотрим еще один пример. Допустим, нам задана функция полезности вида Как выглядят ее кривые безразличия? Согласно стандартным правилам алгебры:

Иными словами, функция полезности v(x₁, x₂) есть просто квадрат функции полезности u(x₁, x₂). Поскольку u(x₁, x₂)  не может быть отрицательной величиной, отсюда следует, что v(x₁, x₂)  является монотонным преобразованием исходной функции полезности u(x₁, x₂). Это означает, что функции полезности должны соответствовать кривые безразличия в точности такой же формы, как у представленных на рис.4.3. Обозначения кривых безразличия будут другими — обозначения 1, 2, 3 теперь станут обозначениями 1, 4, 9, ..., но множество наборов, имеющее полезностьv(x₁, x₂) = 9, в точности такое же, что и множество наборов, имеющее полезность v(x₁, x₂) = 3. Следовательно, v(x₁, x₂) описывает в точности те же предпочтения, что и u(x₁, x₂), поскольку она ранжирует все наборы таким же образом.

Идти в обратном направлении — находить функцию полезности, представляющую определенные кривые безразличия, — несколько сложнее. Для этого можно прибегнуть к двум способам. Первый способ — математический. Исходя из заданных кривых безразличия мы хотим найти функцию, которая принимала бы постоянные значения вдоль каждой кривой безразличия и приписывала бы бóльшие численные значения более высоким кривым безразличия.

Второй способ — несколько более интуитивный. Исходя из описания предпочтений, мы пытаемся представить себе, что именно стремится максимизировать потребитель — какая комбинация товаров описывает его потребительский выбор. Хотя на данной стадии рассмотрения этот способ может показаться несколько неясным, после обсуждения нескольких примеров его смысл станет понятнее.

Совершенные субституты

Помните пример с красными и синими карандашами? Для потребителя имело значение только общее число карандашей. Таким образом, вполне естественно измерять полезность общим числом карандашей. Поэтому предварительно выберем функцию полезности вида u(x₁, x₂) = x₁ + x₂. Подойдет ли она? Достаточно задать себе два вопроса: принимает ли эта функция полезности постоянные значения при перемещении вдоль кривых безразличия? Приписывает ли она более высокие численные значения более предпочитаемым наборам? Поскольку на оба эти вопроса следует дать утвердительный ответ, перед нами — функция полезности.

Разумеется, это не единственная функция полезности, которую мы могли бы использовать в данном случае. Можно было бы также использовать квадрат числа карандашей. Таким образом, функция полезности тоже представляет предпочтения для случая совершенных субститутов, как, впрочем, и любая другая функция, являющаяся монотонным преобразованием функцииu(x₁, x₂).

Что, если потребитель хочет заместить товар 1 товаром 2 в соотношении, отличном от соотношения "один к одному"? Предположим, например, что потребителю потребуются две единицы товара 2, чтобы компенсировать отказ от одной единицы товара 1. Это означает, что товар 1 вдвое ценнее для потребителя, чем товар 2. Функция полезности, следовательно, принимает вид u(x₁, x₂)  = 2x₁ + x₂. Заметьте, что эта функция полезности дает кривые безразличия с наклоном –2.

Вообще предпочтения в отношении совершенных субститутов можно представить функцией вида

u(x₁, x₂)  = ax₁ + bx₂.

Здесь a и b — некие положительные числа, измеряющие "ценность" товаров 1 и 2 для потребителя. Обратите внимание на то, что наклон типичной кривой безразличия задан — a/b.

Совершенные комплементы

Это случай левого и правого башмаков. При предпочтениях такого рода потребителя заботит только число имеющихся у него пар обуви, поэтому естественно выбрать число пар обуви в качестве функции полезности. Число имеющихся у вас полных пар обуви есть минимум числа имеющихся у вас правых x₁ и левых x₂ башмаков. В соответствии с этим функция полезности для совершенных комплементов принимает вид u(x₁, x₂)  = min{x₁, x₂}.

Чтобы проверить, действительно ли эта функция полезности подходит в данном случае, выберем, скажем, товарный набор (10, 10). Добавив еще одну единицу товара 1, получаем набор (11, 10), потребляя который, мы должны были бы остаться на той же самой кривой безразличия. Так ли это? Да, поскольку min{10, 10} = min{11, 10} = 10.

Итак, u(x₁, x₂)  = min{x₁, x₂} — функция полезности, с помощью которой можно описать совершенные комплементы. Как обычно, для этого подойдет и любая функция, являющаяся монотонным преобразованием данной .

Что можно сказать о случае, когда потребитель хочет потреблять товары не в пропорции "один к одному"? Например, как насчет потребителя, всегда потребляющего 2 ложки сахара с чашкой чая? Если x₁ — число имеющихся чашек чая, а x₂ — число имеющихся ложек сахара, то число должным образом чашек подслащенного чая составит

Это несколько сложно для понимания, так что немного поразмыслим об этом. Ясно, что если число чашек чая будет больше половины числа ложек сахара, то мы не сможем положить в каждую чашку чая по 2 ложки сахара. В этом случае у нас в итоге окажется только чашек должным образом подслащенного чая. (Чтобы убедиться в этом, подставьте вместоx₁ и x₂ какие-нибудь числа.)

Разумеется, те же самые предпочтения могут быть описаны любой функцией, которая является монотонным преобразованием указанной функции полезности. Например, можно произвести умножение на 2, чтобы избавиться от дроби. В результате этого получим функцию полезности u(x₁, x₂) = min{2x₁, x₂}.

Вообще, функция полезности, описывающая предпочтения для случая совершенных комплементов, имеет вид

u(x₁, x₂)  = min{ax₁, bx₂},

где a и b — положительные числа, показывающие пропорции, в которых потребляются товары.

Квазилинейные предпочтения

Перед нами форма кривых безразличия, с которой мы раньше не сталкивались. Предположим, что кривые безразличия потребителя представляют собой, как на рис. 4.4, вертикальные смещения одной кривой по отношению к другой. Это означает, что все кривые безразличия являются просто вертикально "смещенными" копиями одной и той же кривой безразличия. Отсюда следует, что уравнение кривой безразличия принимает вид x₂ = k – v(x₁), где k — константа, имеющая для каждой кривой безразличия свои значения. Чем больше значения k, тем выше располагаются кривые безразличия. (Знак "минус" здесь — не более, чем условность; почему он удобен, мы увидим ниже.)

В этой ситуации вполне естественным является ранжирование кривых безразличия по k, или по "высоте" вдоль вертикальной оси. Выразив k и приравняв его к полезности, получаем

u(x₁, x₂) = k = v(x₁) + x₂.

В данном случае функция полезности линейна по товару 2, но нелинейна (возможно) по товару 1; отсюда и название квазилинейная, означающее частично линейную полезность. Конкретные примеры квазилинейной функции полезности: илиu(x₁, x₂) = lnx₁ + x₂. Квазилинейные функции полезности не особенно реалистичны, но с ними легко работать, в чем мы убедимся на нескольких примерах, рассматриваемых далее в этой книге.

Предпочтения Кобба — Дугласа

Другая широко используемая функция полезности — функция полезности Кобба — Дугласа:

где c и d — положительные числа, описывающие предпочтения потребителя¹.

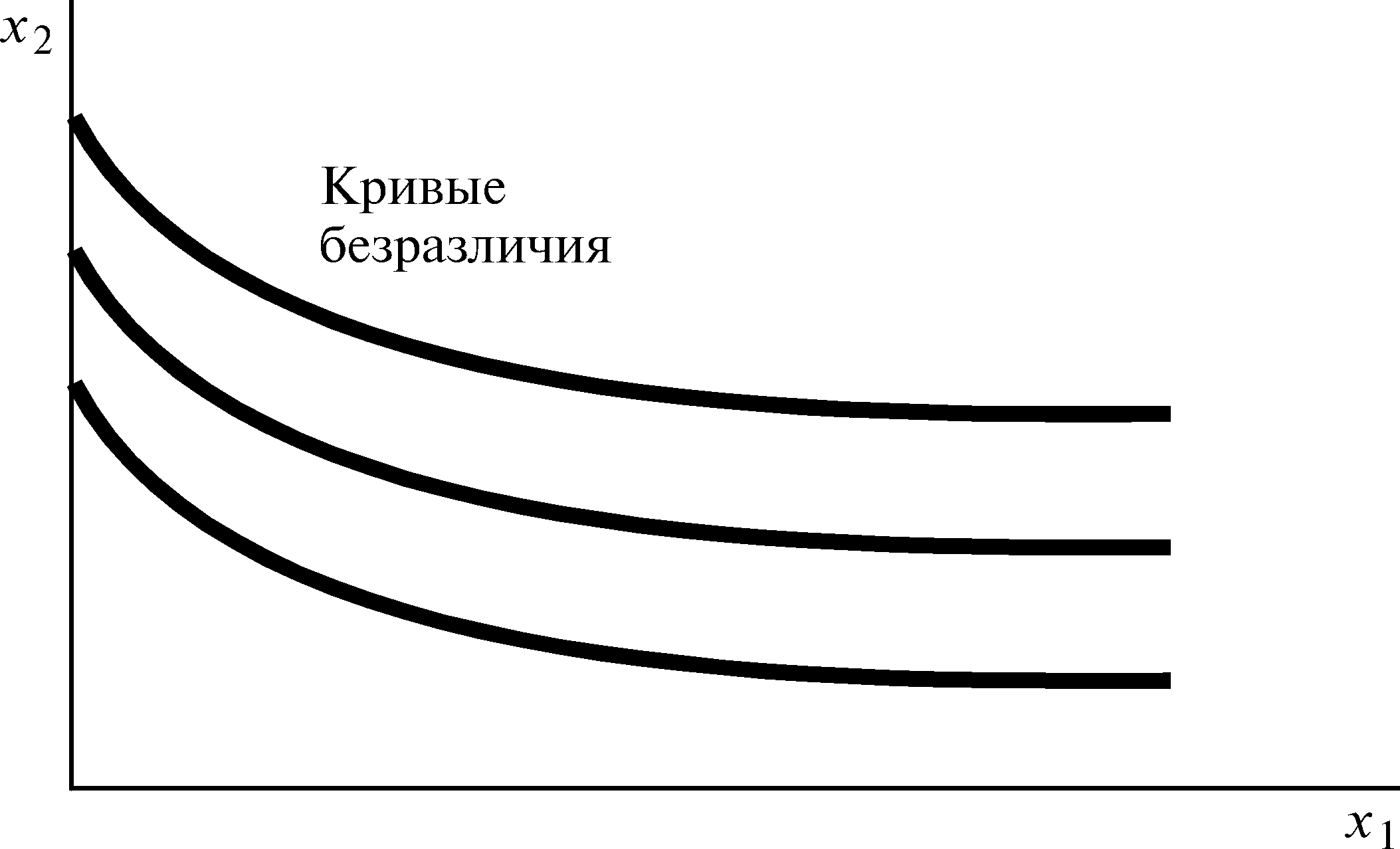
Квазилинейные предпочтения. Каждая кривая безразличия есть вертикально смещенная копия одной-единственной кривой безразличия.

Рис. 4.4

Функция полезности Кобба — Дугласа будет полезна нам при рассмотрении нескольких примеров. Предпочтения, представленные функцией полезности Кобба — Дугласа, в общем виде характеризуются формой кривых безразличия, изображенной на рис. 4.5. На рис.4.5A изображены кривые безразличия для с = 1/2, d = 1/2, на рис.4.5B соответственно для c = 1/5, d = 4/5. Обратите внимание на то, что разные значения параметров c и d обусловливают различие форм кривых безразличия.

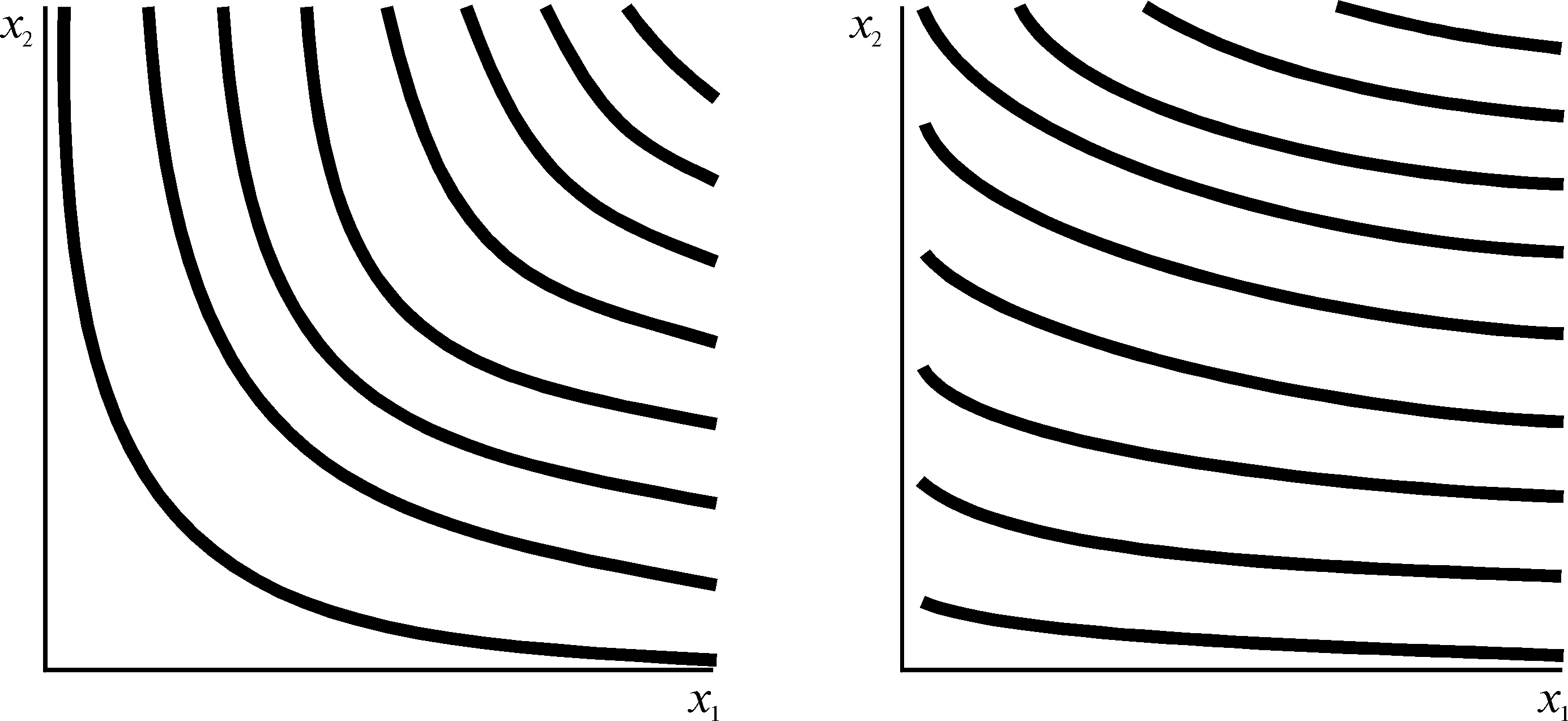
A c = 1/2 d = 1/2 B c = 1/5 d = 4/5

Кривые безразличия Кобба — Дугласа. На рис.A показан случай c = 1/2, d = 1/2, а на рис.B — случай c = 1/5, d = 4/5.

Рис. 4.5

Кривые безразличия Кобба — Дугласа выглядят в точности так же, как симпатичные выпуклые к началу координат монотонные кривые безразличия, которые в гл.3 мы называли стандартными кривыми безразличия. Предпочтения Кобба — Дугласа дают нам типовой пример таких стандартных с виду кривых безразличия, и, действительно, описывающая их формула — это, пожалуй, простейшее алгебраическое выражение, соответствующее стандартным предпочтениям. Предпочтения Кобба — Дугласа окажутся весьма полезными для представления на алгебраических примерах некоторых экономических идей, которые мы рассмотрим позднее.

Разумеется, те же самые предпочтения могут быть представлены и с помощью функции, являющейся монотонным преобразованием функции полезности Кобба — Дугласа, и пару примеров таких преобразований стоит рассмотреть.

Во-первых, если взять натуральный логарифм полезности, то произведение членов превратится в сумму, так что:

Кривые безразличия для этой функции полезности будут выглядеть совершенно так же, как и для первой функции Кобба — Дугласа, поскольку логарифмирование — это монотонное преобразование. (Краткий обзор натуральных логарифмов вы найдете в математическом приложении в конце книги.)

В качестве второго примера предположим, что вначале у нас была функция Кобба — Дугласа вида

Возведя полезность в степень 1/(c + d), получим:

Определим новый член:

Теперь можно записать нашу функцию полезности как

Это означает, что всегда можно произвести такое монотонное преобразование функции полезности Кобба — Дугласа, при котором сумма показателей степени станет равной 1. Позднее станет ясно, что этот факт может иметь полезную интерпретацию.

Функция полезности Кобба — Дугласа может быть представлена различными способами; следует научиться их распознавать, так как данное семейство предпочтений очень полезно для использования в качестве примеров.