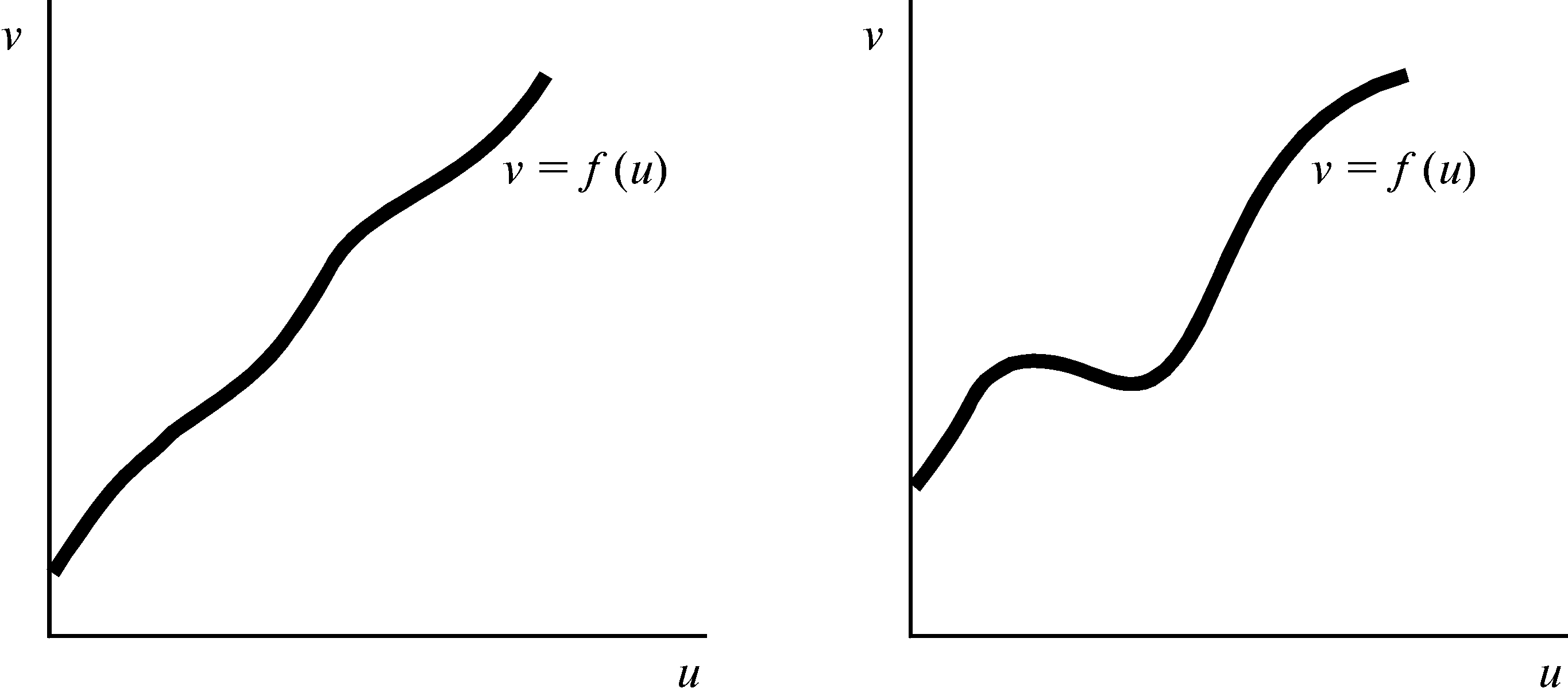Глава 4 полезность
В Викторианскую эпоху философы и экономисты беспечно говорили о "полезности" как о показателе общего благосостояния человека. Полезность представлялась им численной мерой благоденствия индивида. Исходя из этой идеи естественным было полагать, что потребители осуществляют выбор таким образом, чтобы максимизировать свою полезность, т.е. достичь как можно большего удовлетворения.
Беда в том, что эти экономисты классического толка в действительности никогда не приводили описания способа измерения полезности. Как мы должны определять "количество" полезности, связываемое с различными вариантами выбора? Можно ли утверждать, что полезность для одного человека — та же, что и для другого? Что может означать утверждение:" Еще одна плитка шоколада принесет мне вдвое большую полезность, чем еще одна морковь?" Имеет ли понятие "полезность" какое-либо самостоятельное значение, отличное от "того, что люди максимизируют"?
Из-за этих проблем с толкованием понятий экономисты отказались от устаревшей точки зрения на полезность как на меру благоденствия. Вместо этого теория поведения потребителей была полностью переформулирована с позиций потребительских предпочтений, и теперь полезность рассматривают лишь как способ описания предпочтений.
Постепенно экономисты пришли к признанию того, что применительно к потребительскому выбору полезность важна только в том смысле, обладает ли один набор благ более высокой полезностью, чем другой, а насколько более высокой — значения на самом деле не имеет. Первоначально предпочтения определялись в терминах полезности: утверждение, что набор (x1, x2) предпочитается набору (y1, y2) означало, что набор x обладает большей полезностью, чем набор y. Теперь же мы склонны рассуждать наоборот. Описание предпочтений потребителя существенно полезно для анализа потребительского выбора, полезность же — это просто способ описания предпочтений.
Функция полезности — это такой способ приписывания каждому возможному потребительскому набору некоего численного значения, при котором более предпочитаемым наборам приписываются бóльшие численные значения, чем менее предпочитаемым. Иными словами, набор (x1, x2) предпочитается набору (y1, y2) в том и только в том случае, если полезность набора (x1, x2) больше полезности набора (y1, y2): на языке условных обозначений (x1, x2) (y1, y2), если и только если, u(x1, x2) > u(y1, y2).
Единственный смысл приписывания полезности состоит в том, что с его помощью ранжируются товарные наборы. Значение, принимаемое функцией полезности, важно только с точки зрения ранжирования различных потребительских наборов; величина разности полезности двух любых потребительских наборов не существенна. Вследствие указанного акцентирования расположения товарных наборов в определенном порядке полезность этого рода именуется порядковой полезностью.
Рассмотрим, например, табл. 4.1, в которой показано несколько разных способов приписывания полезностей трем товарным наборам, одинаково ранжирующих эти наборы. В данном примере потребитель предпочитает набор A набору B, а набор B — набору С. Все указанные способы приписывания полезностей представляют собой функции полезности, годные для описания одних и тех же предпочтений, потому что все эти функции обладают тем свойством, что набору A поставлено в соответствие бóльшее число, чем набору B, которому в свою очередь поставлено в соответствие бóльшее число, чем набору C.
|
Табл. 4.1 |
Разные способы приписывания полезностей |
|
Набор |
U1 |
U2 |
U3 |
|
A |
3 |
17 |
–1 |
|
D |
2 |
10 |
–2 |
|
C |
1 |
0,002 |
–3 |
Поскольку важен лишь порядок расположения наборов, не может существовать единственного способа приписывания полезностей товарным наборам. Если может быть найден один способ приписывания товарным наборам значений полезности, то можно найти и бесчисленное множество способов сделать это. Если u (x1, x2) — один из способов приписывания значений полезности наборам (x1, x2), то умножение u (x1, x2) на 2 (или на любое другое положительное число) — в свою очередь столь же подходящий способ приписывания им полезностей.
Умножение на 2 — это пример монотонного преобразования. Это такой способ превращения одного множества чисел в другое, при котором порядок чисел сохраняется.
Обычно мы представляем монотонное преобразование функцией f (u), превращающей каждое число u в некоторое другое число f (u) таким способом, при котором порядок чисел сохраняется в том смысле, что u1 u2 подразумевает f (u1) f (u2). Монотонное преобразование и монотонная функция по существу одно и то же.
Примерами монотонных преобразований являются умножение на положительное число (например, f (u) = 3u), прибавление любого числа (напри-мер, f (u) = u + 17), возведение u в нечетную степень (например, f (u) = u3) и т.д.1
Скорость изменения f (u) по мере изменения u может быть измерена изменением f при переходе от одного значения u к другому, отнесенным к изменению u:
![]()
При монотонном преобразовании у f (u2) – f (u1) всегда тот же знак, что и u2 – u1. Следовательно, скорость изменения монотонной функции всегда положительна. Это означает, что график монотонной функции, как показано на рис.4.1A, всегда имеет положительный наклон.