2.3.5.2. Силы в зацеплении гипоидной пары

2.3.5.2.1. Шестерня (рис. 2.6. и 2.7.)

Силы определяются по формулам (3.7), (3.8), (3.9) (с учетом β).

2.3.5.2.2. Колесо

Окружная сила , (3.10)

Осевая сила , (3.11)

Радиальная сила . (3.12)

Рисунок 2.7. - Схема сил, действующих на зубья гипоидной пары

После определения реакций опор, шестерни зубчатого колеса проверяют на прочность, валы главной передачи - на прочность и жесткость по формулам (2.41), (2.43) и (2.44). Долговечность подшипников можно определить по методике, изложенной в пункте 2.2.7.

2.3.5.3. Определение реакции опор

1. При консольном расположении ведущей шестерни (рисунок 2.6.а)

; (3.13)

. (3.14)

2. При расположении ведущей шестерни с дополнительной опорой

; (3.15)

. (3.16)

Напряжения на зубьях шестерен:

1. Напряжение изгиба , (3.17)

- коэффициент формы зуба, l - длина образующей

конуса (рисунок 6, в), t_m – нормальный торцевой модуль.

Допустимые напряжения зависят от ряда факторов (материала, термической обработки и др.) и находятся в пределах 700…900 МПа, большие значения относятся к гипоидным шестерням.

2. Контактные напряжения:

, (3.18)

где ; (3.19)

. (3.20)

Допустимы напряжения до 1000 МПа.

Применяемые материалы шестерен: 20ХН3А, (МАЗ); 20ХНМ (ГАЗ); 30ХГС (ЗИЛ).

2.3.5.4. Расчет ведущего вала главной передачи на жесткость

Ведущий вал главной передачи автомобиля рассчитать на жесткость по величине прогиба в вертикальной плоскости у_в, горизонтальной плоскости у_ги по углу поворотасеченияI–I(рис. 2.6.в) при передаче максимального крутящего момента М_д.мах. В приложении 5 приведены параметры главных передач некоторых моделей отечественных автомобилей.

Расчетная схема (рис. 2.6.а):

; (3.21)

; (3.22)

. (3.23)

Расчетная схема (рис. 2.6.б):

; (3.24)

; (3.25)

. (3.26)

- экваториальный момент инерции сечения сплошного вала.

Задание 2.4 Дифференциалы

2.4.1. Конический дифференциал

Для конического дифференциала (рис. 2.8.) внутреннее передаточное число, т.е. кинематический параметр

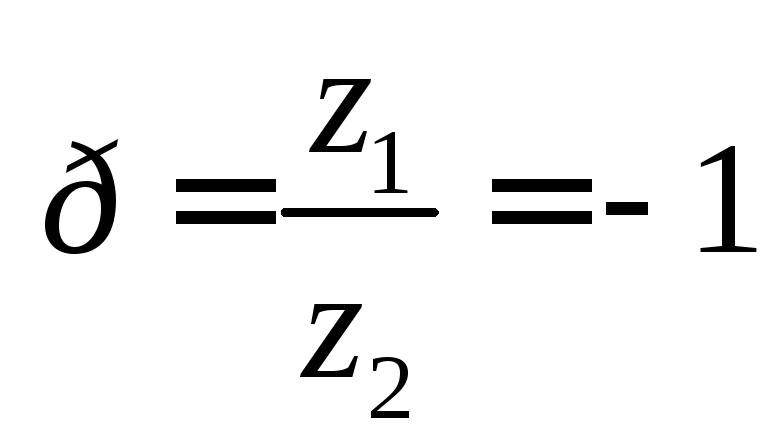, (4.1)

где z₁ иz₂ – число зубьев полуосевых шестерен; знак «-» указывает на вращение выходящих валов в разные стороны при остановленном водиле (в корпусе дифференциала).

Кинематические соотношения в дифференциале:

для симметричного (4.2)

для несимметричного (4.3)

Здесь - кинематический параметр.

Число зубьев сателлитов и полуосевых шестерен может быть четным и нечетным, но для обеспечения сборки должно выполняться условие , (4.4)

где z_ш– число зубьев полуосевой шестерни;n– число сателлитов;

k– целое число.

Рисунок 2.8. - Схемы конических дифференциалов: а– симметричного,б - несимметричного

Силовые соотношения в дифференциале без учета потерь

М₁ = М₂ = 0,5 М_д (для симметричных дифференциалов).

Моменты на полуосях: . (4.5)

Моменты на забегающей полуоси: . (4.6)

Моменты на отстающей полуоси: М_{от .}= 0,5(М_д + М_тр). (4.7)

Здесь М_тр – момент трения в зацеплениях дифференциала.

С достаточным приближением можно считать, что коэффициент блокировки для конического симметричного дифференциала равен единице:

, (4.8)

к = 1 при прямолинейном движении; к = , еслиМ_заб = 0.

Недостаток симметрического дифференциала – снижение проходимости автомобиля, если одно колесо находится в условиях малого сцепления.

Необходимый коэффициент блокировки для заданных условий:

. (4.9)

где ,- коэффициенты сцепления колес автомобиля, находящихся в худших и в лучших условиях сцепления с дорогой соответственно;

f – коэффициент сопротивления качению, если f = 0, то к_блок = 4…5.

В коническом дифференциале определяют нагрузкина зубья сателлитов, полуосевых шестерен, крестовину и нагрузки со стороны сателлитов на корпус дифференциала.

Окружная сила, действующая на один сателлит (рис. 2.9.):

, (4.10)

где r₁– радиус приложения;n_c– число сателлитов.

Напряжения изгиба зубьев могут быть определены по ГОСТ 21354-87. Для сателлита и полуосевых шестерен = (500…800) МПа. Для изготовления зубчатых колес дифференциала используются обычно такие же материалы, что и для главной передачи (цементирование стали марок 18ХГТ, 25ХГТ). Число зубьев сателлитов равно 10…14, а полуосевых шестерен 14…22 с передаточным числом 1,4…2,0.

Шип крестовины под сателлитом испытывает:

Рисунок 2.9. - Схема сателлита

напряжение смятия (4.11) где d –диаметр шипа крестовины, l1- длина посадочного места сателлита, МПа напряжение среза (4.12) =(100…120) МПа,

3) напряжение смятия в месте крепления в корпусе дифференциала под действием окружной силы

, (4.13)

где r₂- радиус приложения.

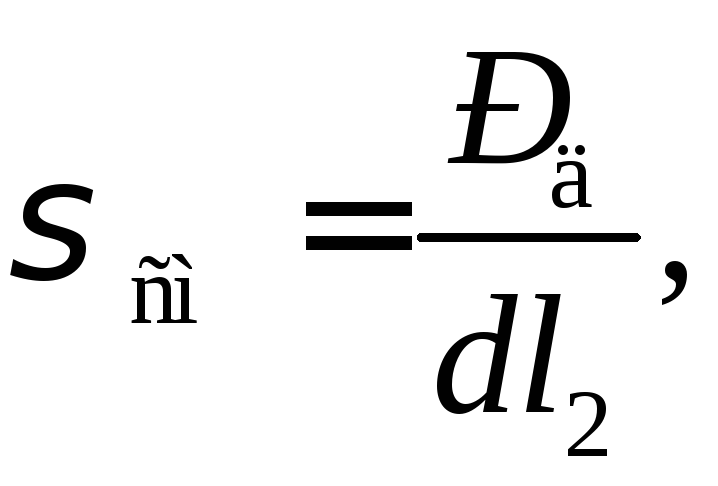МПа (4.14)

где l₂ - длина крестовины в корпусе дифференциала. [] = (50…60).

Давление торца сателлита на корпус дифференциала (рисунок 9) определяется напряжением смятия

, (4.15)

где - опорная поверхность сателлита;- угол зацепления,= 30…40° - половина угла конуса сателлита,МПа.