
- •Содержание
- •Введение
- •1 Структурный анализ рычажного механизма
- •2 Кинематический анализ механизма
- •2.1 Построение планов положений механизма
- •2.2 Построение планов аналогов скоростей
- •2.3 Построение планов аналогов ускорений
- •2.4 Построение кинематических диаграмм перемещений, скоростей, ускорений выходного звена
- •3. Динамический анализ механизма
- •3.1 Определение приведённого момента сил сопротивленияи приведённого момента движущих сил
- •3.2 Определения работы движущих сил
- •3.3 Определение переменной составляющей приведённого момента инерции
- •3.4 Определение постоянной составляющей приведённого момента инерции и момента инерции маховика.
- •3.5 Определение закона движения звена приведения
- •4. Силовой анализ
- •4.1 Кинематический анализ механизма
- •4.2 Построение плана скоростей
- •4.3 Построение плана ускорения
- •4.4 Определение сил инерции и моментов сил инерции звеньев
- •4.5 Кинетостатический силовой анализ механизма
- •4.5 Определение уравновешивающей силы методом Жуковского.
- •5 Синтез кулачкового механизма
- •5.1 Определение кинематических характеристик толкателя
- •5.2 Определение основных размеров кулачкового механизма
- •5.3 Построение профиля кулачка
- •5.4 Определение углов давления
- •6 Синтез передаточного зубчатого механизма
- •6.1 Подбор чисел зубьев и числа сателлитов планетарного механизма
- •6.2 Расчет параметров эвольвентного зацепления
- •6.3 Определение коэффициента полезного действия зубчатого механизма
- •Список использованных источников
4. Силовой анализ
4.1 Кинематический анализ механизма
Изображаем схему механизма в положении
4. Для положения 4 ранее были получены:

4.2 Построение плана скоростей
Скорость точки A равна:

Принимаем
отрезок
 равный 70 мм;
равный 70 мм;
Тогда
масштабный коэффициент скорости
 ,
равен:
,
равен:
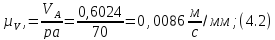
Так
как
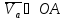 и направлена в сторону вращения кривошипа,
то откладываем отрезок
и направлена в сторону вращения кривошипа,
то откладываем отрезок (для соответствующего положения
кривошипа).
(для соответствующего положения
кривошипа).
Для построения планов скоростей группы Асcура 2,3 необходимо определить положение точки B. Для этого составим два векторных уравнения:

Где
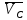 =0,
точкаC
являющаяся стойкой совпадает с полюсом.
=0,
точкаC
являющаяся стойкой совпадает с полюсом.
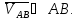
 где
где
 соответственно.
соответственно.
В соответствии с уравнениями (2.4) из точки а проводим перпендикуляр к звену AB, а из точки p перпендикуляр к звену CB. На пересечении обозначаем точку b.
Точку D принадлежащую 3-ему звену строим на продолжении отрезка ab по теореме подобия.
Длину
отрезка
 находим из подобия:
находим из подобия:
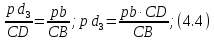
Длина отрезка pbберётся из плана скоростей, аCDиCBиз плана положений механизма.
Для нахождения точки Dпринадлежащей 5 звену составим два векторных уравнения:

Где

 скорости точкиD5относительно точкиD3иCсоответственно.
скорости точкиD5относительно точкиD3иCсоответственно.
Согласно данным векторным уравнениям (4.5) из точки d3проводим отрезок перпендикулярный звенуCD, а из точкиpпроводим отрезок параллельный направляющей ползуна до пересечения с перпендикуляром из точкиd3. На пересечении обозначаем точкуd5.
Точки S2иS3находим по теореме подобия:
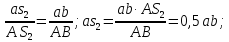 (4.6)
(4.6)
 (4.7)
(4.7)
Из плана скоростей находим линейные:



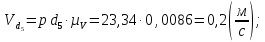


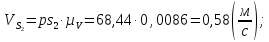
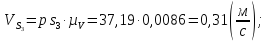
Угловые скорости звеньев 2 и 3, которые движутся плоскопараллельно, находим по следующим формулам:


4.3 Построение плана ускорения
Ускорение точки A:
 (4.10)
(4.10)
где:
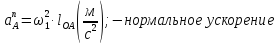
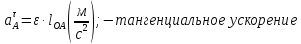
Тангенциальное
ускорение направлено перпендикулярно
ОAв сторону углового
ускорения


Определив модуль ускорения точки A,
на плане ускорений, из полюса π проведём
отрезок ,
равный 100 мм. Далее рассчитаем масштабный
коэффициент ускорений:
,
равный 100 мм. Далее рассчитаем масштабный
коэффициент ускорений:
 (4.12)
(4.12)
Вектор
 является планом ускорения кривошипаOAи направлен параллельно
звену от точкиAк точкеO.
является планом ускорения кривошипаOAи направлен параллельно
звену от точкиAк точкеO.
Для построения точки Bна плане ускорений необходимо составить два векторных уравнения, рассматривающих положение точки относительно точкиAи стойкиC.

где:
 - нормальное ускорение точкиBотносительноA.
- нормальное ускорение точкиBотносительноA.
 - нормальное ускорение точкиBотносительно С.
- нормальное ускорение точкиBотносительно С.

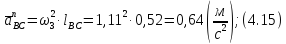
Вектор ускорения
 на плане изображается отрезком
на плане изображается отрезком ,
а вектор ускорения
,
а вектор ускорения отрезком
отрезком :
:
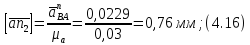

Так как отрезок
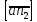 меньше
одного миллиметра то, принимаем, что
точка
меньше
одного миллиметра то, принимаем, что
точка совпадает с точкойaна
плане ускорений.
совпадает с точкойaна
плане ускорений.
Далее решим векторные уравнения
графически. Для этого по первому
векторному уравнению через точку
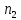 проведем перпендикуляр к звенуAB,
являющийся вектором
проведем перпендикуляр к звенуAB,
являющийся вектором .
.
По второму векторному уравнению из
полюса π (т.к.
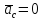 )
проведём вектор
)
проведём вектор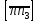 ,
паралелный звенуBCиз
точкиBк С. Далее через
точку
,
паралелный звенуBCиз
точкиBк С. Далее через
точку проведём перпендикуляр к звенуBC,
который является вектором
проведём перпендикуляр к звенуBC,
который является вектором .
.
Точка пересечения векторов
 и
и будет определять направление и величину
полного ускорения точкиB.
будет определять направление и величину
полного ускорения точкиB.

Модуль тангенциального ускорения относительно точки A:
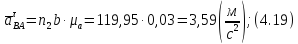
Модуль тангенциального ускорения относительно точки C:

Точка
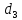 на плане ускорений находим по теореме
подобия. Вектор этого ускорения
откладываем на продолжении вектора
на плане ускорений находим по теореме
подобия. Вектор этого ускорения
откладываем на продолжении вектора .
Длина отрезка рассчитывается по формуле:
.
Длина отрезка рассчитывается по формуле:

Рассмотрим
построение точки
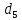 ,
являющейся выходным звеном механизма
(ползуном). Для этого из точки
,
являющейся выходным звеном механизма
(ползуном). Для этого из точки проводим линию перпендикулярную
направляющей ползуна, а из точки
проводим линию перпендикулярную
направляющей ползуна, а из точки линию параллельную направляющей ползуна.
Точка пересечения этих линий будет
определять величину и направление
полного ускорения точки
линию параллельную направляющей ползуна.
Точка пересечения этих линий будет
определять величину и направление
полного ускорения точки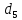 :
:

Для построения точек
 используем теорему подобия. Длины
отрезков определяем по формулам
используем теорему подобия. Длины
отрезков определяем по формулам
 (4.23)
(4.23)

Для определения ускорений центров масс, необходимо из полюса π провести прямые к этим точкам, которые будут являться векторами полных ускорений этих точек. Численные значения этих ускорений рассчитаем по формулам


Точка
 на плане ускорений совпадает с точкой
на плане ускорений совпадает с точкой ,
т.к. она совершает плоское движение.
,
т.к. она совершает плоское движение.
Далее определяем величины угловых ускорений звеньев 2 и 3 по формулам:


Направления угловых скоростей определяем,
перенеся векторы
 и
и в точкуBи рассмотрев
вращения соответствующих звеньев вокруг
этой точки.
в точкуBи рассмотрев
вращения соответствующих звеньев вокруг
этой точки.
