Тема 6. Методи аналізу рядів розподілу

План вивчення теми

6.1.Поняття та основні складові рядів розподілу. Види рядів розподілу, основні методи їх побудови

6.2.Характеристики центру розподілу і порядкові статистики (середня, мода, медіана, їх взаємозв’язок; квантилі розподілу - квартилі, квінтилі, децилі, перцентилі) та їх роль в аналізі закономірностей розподілу

6.3.Характеристики вимірювання варіації ознак - абсолютні та відносні міри варіації (розмах варіації, середнє лінійне та середнє квадратичне відхилення, коефіцієнти варіації). Варіація альтернативної ознаки

6.4.Характеристики форми розподілу: коефіцієнти асиметрії та ексцесу

6.5.Показники диференціації та концентрації

Після вивчення теми студенти повинні:

знати: в чому полягають аналітичні функції рядів розподілу, основні їх види та методи побудови; методологічні аспекти вимірювання закономірностей розподілу: центру розподілу, варіації ознак, форми розподілу й диференціації та концентрації;

уміти: аналізувати закономірності розподілу, оцінювати, відповідно до мети дослідження, ступінь варіації ознак і однорідність сукупності, симетричність і рівномірність розподілу, оцінювати інтенсивність структурних зрушень; виявляти закони розподілу тощо.

Бібліографічний список: [7 – 10; 17 - 22 ]

6.1. Поняття та основні складові рядів розподілу. Види рядів розподілу, основні методи їх побудови

Статистичний ряд розподілу – упорядкований розподіл одиниць сукупності, що вивчається, на групи за певною варіативною ознакою. Наприклад, розподіл працівників підприємства за рівнем кваліфікації. В даному разі варіативною ознакою буде кваліфікація працівника (якісна ознака). Якщо вивчати обсяги виготовленої продукції або проданих товарів, то варіативною ознакою буде кількість продукції чи товарів або їх вартість (кількісна ознака). Статистичний ряд розподілу характеризує склад явища, що вивчається, дозволяє судити про однорідність чи неоднорідність сукупності, закономірності розподілу, межі варіації одиниць сукупності тощо.

Ряди розподілу, які побудовані за атрибутивними ознаками, називаються атрибутивними. В таких рядах порядок розташування елементів сукупності,

що вивчається, не має значення. Наприклад, розподіл працівників підприємства за професією. Ряди розподілу, які побудовані за кількісними ознаками в порядку зростання чи зниження їх значень, називаються варіаційними.

64

Ряд розподілу складається з двох елементів: варіанти та частоти. Числові значення кількісної ознаки (варіанти) можуть бути додатними і від’ємними, абсолютними і відносними. Наприклад, якщо досліджується ефективність діяльності фірми чи підприємства, то додатна величина характеризує поліпшення, а від’ємна – погіршення роботи; якщо досліджуються результати економічної діяльності фірми чи підприємства, то додатна величина характеризує прибутки, а від’ємна – збитки.

Частоти – це числа, що показують, скільки разів зустрічається та чи інша варіанта в ряді розподілу (якщо мова йде про дискретну величину), або скільки варіант потрапляють в певний інтервал (якщо мова йде про неперервну величину). Підсумок всіх частот складає обсяг сукупності і визначає кількість елементів всієї сукупності, що вивчається.

Іноді у варіаційних рядах замість частот використовують частки – це частоти, подані у вигляді відносних величин (як частина одиниці або у відсотках). Підсумок часток відповідно дорівнює одиниці або 100 %. Заміна частот частками дозволяє порівнювати варіаційні ряди з різним обсягом сукупностей.

Варіаційні ряди залежно від характеру варіації поділяються на дискретні та інтервальні. Дискретні варіаційні ряди ґрунтуються на ознаках, виражених дискретними величинами. Наприклад, розподіл сімей за числом дітей у сім’ї.

Інтервальні варіаційні ряди ґрунтуються на ознаках, виражених неперервними величинами або дискретними величинами, значення яких варіюють у досить широких межах і можуть бути наведені у вигляді інтервалів. Наприклад, такі ознаки, як вартість товару або його вагу, зручніше наводити інтервальними варіаційними рядами.

Для графічного зображення рядів розподілу застосовуються такі діаграми, як полігон, гістограма та кумулятивний полігон.

Якщо первинний ряд містить велику кількість варіант, то його безпосередній розгляд не дає уявлення про розподіл одиниць за значеннями ознаки в сукупності. Тому першим кроком в упорядкуванні первинного ряду є його ранжирування, тобто розподіл всіх варіант в порядку зростання або зниження числового значення ознаки.

Варіаційний ряд розподілу прийнято оформляти у вигляді таблиці, що складається з двох граф чи двох рядків; в одній наведені варіанти (ліва графа, якщо таблиця має вертикальне розташування, і верхній рядок, якщо таблиця розташовується горизонтально), в іншій наводяться частоти або частки.

Побудова дискретного варіаційного ряду з невеликим числом варіант не викликає ніяких ускладнень. Наприклад, розподіл студентів академічної групи за оцінкою, яку вони одержали на іспитах з певної дисципліни (табл. 6.1).

Для побудови ряду розподілу неперервних величин, або дискретних, наведених у вигляді інтервалів, необхідно виявити оптимальну кількість груп (інтервалів), на які слід розтинати сукупність, що вивчається.

Питання щодо кількості груп і розміру інтервалів слід вирішувати з урахуванням багатьох обставин, перш за все залежно від мети дослідження, значення ознаки, що вивчається та таке інше. Чим більше створено груп, тим менший розмір інтервалу, і навпаки.

65

Таблиця 6.1

Розподіл студентів групи ЕП-06-3 за результатами здачі іспиту з дисципліни “Статистика” (дані умовні)

Кількість груп залежить від обсягу сукупності, що вивчається, і ступеню коливання групувальної ознаки. Якщо обсяг сукупності невеликий, то не можна створювати велику кількість груп, бо групи будуть містити малу кількість елементів. Але нове, прогресивне, поки воно ще не стало масовим, завжди проявляється в малому числі фактів, і статистика повинна враховувати ці випадки. Таким чином, у процесі вирішення питання щодо чисельності груп треба керуватися знанням суті явища, що вивчається. На кількість груп суттєво впливає ступінь коливання групувальної ознаки: чим він більше, тим більше груп треба створювати. Приклад інтервального ряду розподілу наведено в табл. 6.2.

Таблиця 6.2

Розподіл книжок за їх ціною у книжковому відділі магазину на 01.01.2008 (дані умовні)

Для дискретних рядів розподілу застосовується графік у вигляді полігону.

Наприклад, розподіл робітників складального цеху за кваліфікацією, наведений нижче в таблиці, можна подати у вигляді полігону розподілу – лінійна діаграма.

Розподіл робітників складального цеху за кваліфікацією

66

Для графічного зображення інтервальних рядів розподілу застосовується гістограма, вигляд якої наведено на рис. 6.1. Наприклад, розподіл товару за ціною, , наведений нижче в таблиці, можна подати у вигляді гістограми.

Кількість товару, f

Рис. 6.1. Розподіл дитячого одягу у крамниці за його ціною

Для побудови кумулятивного полігону використовуються суми накопичених частот (або суми накопичених часток, якщо в ряді розподілу замість частот використовуються частки). У цьому разі за віссю абсцис відкладаються значення ознаки, а за віссю ординат – кумулятивні частоти. Кумулятивні частоти (частки) одержуються накопиченим підсумком, тобто до попереднього значення додається наступне і значення одержаної суми відкладається на осі ординат. Максимальне значення характеризує обсяг сукупності або дорівнює одиниці у разі застосування накопичених часток.

Кумулятивний полігон можна побудувати у вигляді ламаної лінії (для дискретної ознаки) або у вигляді ступінчатої гістограми (для неперервної ознаки).

Для побудови кумулятивного полігону, наприклад, для дискретного ряду розподілу, наведеного в табл. 6.1, спочатку слід обчислити суму накопичених частот. Цей показник обчислюється за формулою:

де Si – сума накопичених частот до і-ї ознаки включно; fi – значення частоти і-ї ознаки.

Визначивши суми накопичених частот для кожної ознаки, табл. 6.1 матиме такий вигляд:

67

Таблиця 6.3

Розподіл студентів групи ЕП-06-3 за результатами здачі іспиту з дисципліни “Статистика” (дані умовні)

Графічне зображення ряду розподілу побудованого за накопиченими частотами матиме вигляд кумулятивного полігону. Аналогічно будується кумулятивний полігон для інтервального ряду розподілу. У даному разі табл. 6.2 матиме вигляд, наведений у табл. 6.4. і графічно - на рис. 6.2.

Таблиця 6.4

Розподіл книжок за їх ціною у книжковому відділі магазину на 01.01.2008 (дані умовні)

Рис. 6.2. Кумулятивний полігон, побудований за розподілом книжок за їх ціною у книжковому відділі магазину на 01.01.2008

68

На рис. 6.2 кумулятивний полігон виділено жирною лінією. Як видно, у даному разі кумулятивний полігон починається не з центру системи координат, а з точки на осі абсцис, яка відповідає нижній межі першого інтервалу ряду розподілу.

Основні принципи та методика побудови рядів розподілу наведено у підрозділі 3.3. «Методологічні засади побудови статистичних групувань» теми 3.

6.2. Характеристики центру розподілу і порядкові статистики (середня, мода, медіана, їх взаємозв’язок; квантилі розподілу - квартилі, квінтилі, децилі, перцентилі) та їх роль в аналізі закономірностей розподілу

Виявлення закономірностей зміни частот залежно від зміни варіативної ознаки, що покладена в основу групування і є основою аналізу варіаційних рядів розподілу. При такому аналізі найчастіше використовують такі групи показників:

характеристики центру розподілу;

характеристики розміру варіації;

характеристики форми розподілу.

Центром розподілу називається значення варіативної ознаки, навколо якого групуються інші варіанти. До характеристик центру розподілу належать

середня, мода, медіана, чверть (квартиль) і десята частина (дециль).

Види та методика визначення середньої величини детально розглянуто у попередній темі. Для повнішого розкриття властивостей ряду розподілу визначають моду Мо, медіану Ме, квартилі Qu1, Qu2, Qu3 та децилі – від D1 до D9.

Мода (Мо) – значення варіанти, яке найчастіше повторюється в ряду розподілу. У дискретних рядах моду легко відшукати візуально, безпосередньо за найбільшим значенням частоти або частки.

В інтервальному ряді за тим самим принципом визначається модальний інтервал, тобто інтервал, частота якого має найбільше значення. Якщо треба більш точно встановити модальний рівень, його обчислюють за формулою:

х Мо – нижня межа модального інтервалу h Mo – ширина модального інтервалу

f Mo – частота модального інтервалу

f Mo – 1 – частота попереднього (перед модального) інтервалу f Mo + 1 – частота наступного (після модального) інтервалу.

Слід зауважити, що ця формула використовується для інтервальних варіаційних рядів з рівними інтервалами. Визначення моди в ряді розподілу із нерівними інтервалами має свої особливості.

Для визначення моди за інтервальним варіаційним рядом з нерівними інтервалами в аналітичному вираженні перегруповують вихідний варіаційний ряд на ряд з рівними інтервалами або замість частот використовують відносні

69

частоти. Для визначення моди графічним способом будують гістограму відносних частот. Основу прямокутників становлять розміри інтервалів, а висоту – відношення відповідної частоти до ширини інтервалу. Для кожного інтервалу визначається відносна частота за формулою:

w i fi , h i

де wi – відносна частота i–го інтервалу; fi – частота i–го інтервалу;

hi – ширина i–го інтервалу.

Принцип визначення моди лишається тим самим, що й для інтервального варіаційного ряду з рівними інтервалами.

Графічним методом мода визначається за допомогою гістограми. Графічним методом мода визначається так: на гістограмі (рис. 6.3) беремо

прямокутник з найбільшою висотою, лівий верхній кут цього прямокутника (точка B) з’єднуємо з лівим верхнім кутом прямокутника, розташованого праворуч (точка D), а верхній правий кут найбільшого прямокутника (точка С) з’єднуємо з правим верхнім кутом прямокутника, розташованого ліворуч (точка А); з перетину прямих АС і BD (точка М) на вісь абсцис опускаємо перпендикуляр, який і визначить значення моди.

f

50

Рис. 6.3. Визначення моди графічним методом

Медіана (Ме) – варіанта, що ділить упорядкований варіаційний ряд на дві, рівні за обсягом частини. Наприклад, якщо в ряді розподілу робітників за віком Ме = 30, це означає, що половина робітників мають вік менше 30 років, половина – старші за цей вік.

Визначаючи медіану, використовують кумулятивні частоти Sfi або частки Sdi. У дискретному ряді медіанним буде значення ознаки, кумулятивна частота якого перевищує половину сукупності, тобто Sfi ≥ 0,5 fi (для кумулятивної частки Sdi ≥ 0,5). Кумулятивні частоти визначаються доданням наступного значення частоти до суми значень попередніх частот. При цьому не має значення які інтервали у варіаційному ряді розподілу: рівні чи нерівні.

70

В інтервальному ряді за цим принципом визначають медіанний інтервал. Значення медіани, як і значення моди, обчислюють за інтерполяційною

формулою:

хМе – нижня межа медіанного інтервалу hMe – ширина медіанного інтервалу 0,5 f i – половина сукупності

S fMe - 1 – сума накопичених частот до медіанного інтервалу f Ме – частота медіанного інтервалу.

Медіану можна визначити графічним способом, використовуючи для цього кумулятивний полігон. Медіана графічним способом визначається так: для визначення медіани графічним методом використовують графік, побудований на основі накопичених частот або часток. Цей графік має вигляд кумулятивної гістограми із вбудованою кумулятою. На осі ординат відкладають точку, що дорівнює половині суми частот. З цієї точки проводять лінію, паралельну осі абсцис до її перетину з лінією кумулятивного полігону (точка А). З точки А на вісь абсцис опускають перпендикуляр, координата якого і буде медіаною. Приклад графічного визначення медіани наведено на рис. 6.4.

Результати розрахунків свідчать про те, що типовим рівнем ціни товару є

x = 44 грн.; половина одиниць товару мають значення ціни, що дорівнює або менше ніж 46 грн., а інша половина - дорівнює або більше ніж 46 грн.

Рис. 6.4. Визначення медіани графічним методом

В аналізі закономірностей розподілу крім медіани використовуються також й інші структурні (або порядкові) характеристики, які ділять всі одиниці розподілу на рівні за чисельністю групи. Вони отримали загальну назву

71

квантилі. Частинним випадком квантилів є, насамперед, квартилі, квінтилі, децилі та перцентилі (діле сукупність на сто рівних частин).

Квартилі – це варіанти, які ділять обсяг сукупності на чотири рівних частини. Існують три квартилі. У загальному вигляді значення і-го квартиля визначається за формулою:

де Quі – і-й квартиль;

xQu і – нижня межа і-го квартильного інтервалу;

h Qu і – ширина інтервалу, де розташований і-й квартиль;fi / 4 – чверть сукупності;

SQu і – 1 – сума накопичених частот до інтервалу, де розташований і-й квартиль; fQu і – частота інтервалу, де розташований і-й квартиль.

і – порядковий номер квартиля.

Слід зауважити, що в тому разі, якщо перший квартиль (або інший структурний показник: медіана, квінтиль чи дециль) потрапляють до першого інтервалу, то попередня сума накопичених частот дорівнює нулю. Квартилі так само як медіану можна визначити графічним способом за допомогою кумулятивного полігону. Для цього за віссю ординат відкладають відповідні точки, з яких проводять лінії паралельно осі абсцис до перетину з кумулятивним полігоном (відповідно точки А, В, С). Далі з точок (А, В, С) опускають перпендикуляри на вісь абсцис та отримують відповідні значення квартилів (див. рис. 6.5).

Sf

Рис. 6.5. Визначення квартилів графічним способом

72

Квінтилі – це варіанти, які ділять обсяги сукупності на п’ять рівних частин. Існує чотири квінтиля. Значення і-го квінтиля визначається за формулою:

де Qwі – перший квінтиль;

xQw і – нижня межа першого квінтиля;

h Qw і – ширина інтервалу, де розташований перший квінтиль; 0,2 fi – одна п’ята сукупності;

і – порядковий номер квінтиля;

SQw і – 1 – сума накопичених частот до інтервалу, де розташований перший квінтиль;

fQw і – частота інтервалу, де розташований перший квінтиль.

Графічним способом визначення квінтилів виконують аналогічно представленню квартилів.

Децилі – це варіанти, які ділять обсяги сукупності на десять рівних частин. Існує дев’ять децилів, що визначаються за формулою, яка в загальному вигляді має таке вираження:

де і – порядковий номер дециля; xDe i – нижня межа і-го дециля;

h De i – ширина інтервалу, де розташований і-й дециль; 0,1 fi – одна десята сукупності;

SDe i – 1 – сума накопичених частот до інтервалу, де розташований і-й дециль; fDe i – частота інтервалу, де розташований і-й дециль.

Децилі також можна визначити графічним способом за допомогою кумулятивного полігону.

6.3. Характеристики вимірювання варіації ознак - абсолютні та відносні міри варіації (розмах варіації, середнє лінійне та середнє квадратичне відхилення, коефіцієнти варіації). Варіація альтернативної ознаки

Варіація, тобто коливання, мінливість будь-якої ознаки є властивістю статистичної сукупності. Здатність ознаки змінювати індивідуальні значення називається варіабельністю. Вона зумовлена дією безлічі взаємопов’язаних причин, серед яких є основні та другорядні. Основні причини формують центр розподілу. Другорядні причини впливають на форму розподілу.

73

Для виміру та оцінки варіації використовують систему абсолютних та відносних характеристик. До абсолютних характеристик належать: розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення та дисперсія. До відносних характеристик варіації належать різноманітні коефіцієнти, найбільш поширене використання серед яких мають коефіцієнти варіації, що побудовані на відношенні абсолютних характеристик з середньою арифметичною. Кожна з названих характеристик має певні аналітичні переваги під час вирішення тих чи інших завдань статистичного аналізу.

Методика обчислення характеристик варіації залежить від виду ознаки Х та наявних даних (первинні чи похідні, згруповані чи ні).

Розмах варіації – різниця між найбільшим і найменшим значеннями ознаки, розраховується за формулою:

R = X max – X min,

де X max – максимальне значення ознаки X min – мінімальне значення ознаки.

Розмах варіації характеризує межі, в яких змінюється кількісне значення ознаки. Цей показник встановлює крайні числові значення варіант, що складають досліджувану сукупність.

В інтервальному ряді розподілу розмах варіації визначають як різницю між верхньою межею останнього інтервалу та нижньою межею першого. Проте, якщо інтервал відкритий, для обчислення розмаху варіації використовується середина інтервалу. Звичайно, спочатку інтервал має бути закритим згідно з відповідними правилами.

Крім розмаху варіації, у практиці статистичного аналізу широко застосовують інші абсолютні характеристики варіації, що ґрунтуються на відхиленнях індивідуальних значень ознаки від середньої арифметичної.

Оскільки відповідно до першої властивості середньої арифметичної( Х і – Х ) = 0, то при розрахунку такого роду характеристик використовують або модулі, або квадрати відхилень. У результаті маємо такі характеристики варіації: середнє лінійне відхилення, середнє квадратичне відхилення та дисперсію. Розрахункові формули цих показників наведені в табл. 6.5.

Якщо статистична сукупність надана у вигляді інтервального варіаційного ряду, то для розрахунку показників варіації використовуються розрахункові формули за зваженою формою. При цьому замість індивідуального значення ознаки обирається середина відповідного інтервалу.

Середнє лінійне відхилення являє собою середню відстань між середньою арифметичною величиною та відповідними індивідуальними значеннями окремих ознак, а це завжди додатна величина. Саме тому у формулах відхилення кожної варіанти від середньої арифметичної береться за модулем.

Дисперсія являє собою середній квадрат відхилень, є відповідні властивості дисперсії і вона пов’язана з середнім квадратичним відхиленням таким співвідношенням:

74

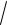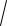D 2 ,

де – середнє квадратичне відхилення D = 2 – дисперсія.

Таблиця 6.5

Показники варіації та формули для їх розрахунку

хі – індивідуальні значення окремої ознаки, варіанти

х – середня арифметична (середнє значення ознаки) n – обсяг сукупності, кількість ознак у сукупності fi – частота відповідної ознаки.

При порівнянні варіації різних ознак або однієї ознаки у різних сукупностях використовуються відносні характеристики: коефіцієнти варіації. До них належать:

лінійний коефіцієнт варіації, який обчислюється за формулою:

де l – середнє лінійне відхилення

х– середня арифметична;

квадратичний коефіцієнт варіації, який обчислюється за формулою:

де – середнє квадратичне відхиленнякоефіцієнт осциляції, який обчислюється за формулою:

R

V R x ,

де R – розмах варіації.

75

Чим менше середнє відхилення, тим більш типова середня, тим більш однорідна сукупність. Найчастіше квадратичний коефіцієнт варіації використовують як критерій однорідності сукупності, він є ознакою надійності середньої.. У симетричному, близькому до нормального, розподілі Vσ = 0,33.

Для малих сукупностей розрізняють такі значення відносних коливань: Vσ < 10% - незначне коливання, сукупність однорідна, значення

середньої є типовим рівнем ознаки в даній сукупності;

10 % ≤ Vσ ≤ 33% - середнє коливання, сукупність в межах однорідності, значення середньої можна вважати типовим рівнем ознаки в даній сукупності;

Vσ > 33% - високий рівень варіації, сукупність неоднорідна, значення середньої неможна вважати типовим рівнем ознаки в даній сукупності.

Середнє квадратичне відхилення також пов’язане з середнім лінійним відхиленням. За правилом мажорантності середніх > l . Якщо обсяг сукупності досить великий і розподіл ознаки наближається до нормального, то між середнім квадратичним та середнім лінійним відхиленнями існує такий взаємозв’язок:

Дисперсія, або середній квадрат відхилення ( 2 ), посідає особливе місце в статистичному аналізі соціально-економічних явищ. Завдяки своїм математичним властивостям, вона має важливе значення не лише під час вивчення варіації, але є невід’ємним і важливим елементом інших статистичних методів аналізу, зокрема, вибіркового, дисперсійного та кореляційнорегресійного.

Дисперсію використовують не лише для оцінки варіації, а й для вимірювання взаємозв’язків, для перевірки статистичних гіпотез тощо.

Для ознак метричної шкали дисперсія є базою для обчислення середнього квадратичного відхилення, оскільки D 2 , і залежно від наявних даних може бути простою (для не згрупованих даних):

2 ( xi x) 2 n

або зваженою (для згрупованих даних):

2 ( xi x) 2 fi ,

fi

де хі – індивідуальні значення окремої ознаки, варіанти

х – середня арифметична (середнє значення ознаки)

76

n – обсяг сукупності, кількість ознак у сукупності fi – частота відповідної ознаки.

Дисперсія має певні математичні властивості:

1. Якщо кожну варіанту зменшити або збільшити на одну й ту саму величину А, дисперсія не зміниться. Математично це записується у такому вигляді:

x i A x A 2 D . n

2. Якщо кожну варіанту збільшити або зменшити в k разів, то дисперсія зміниться в k 2 разів:

k x i k x 2 k 2 D . n

3. Якщо частоти замінити частками, дисперсія не зміниться. Математично це виражається так:

Нескладними алгебраїчними перетвореннями можна довести, що дисперсія – це різниця квадратів, а саме різниця між середнім квадратом і квадратом середньої величини:

n

де х і – значення окремої ознаки

n – обсяг сукупності (кількість ознак).

Дисперсія альтернативної ознаки обчислюється як добуток часток за формулою:

2 d1 d0 ,

де d 1 – частка елементів сукупності, яким властива ознака

d 0 – частка решти елементів, у яких відсутня ознака (d 0 = 1 – d 1).

Дисперсія альтернативної ознаки широко використовується під час проектування вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо.

77

Рис. 6.9. Види розподілу:

–- лівостороння (від’ємна) асиметрія (Мо > Ме > х ).

Стандартизовані відхилення, які мають назву коефіцієнта асиметрії, характеризують напрям та міру скошеності розподілу і розраховуються за формулами:

Якщо має місце відхилення коефіцієнта асиметрії від нуля в той чи інший бік, то можна вести мову про більшу чи меншу асиметрію. Вважають, що при

Характеристики центру розподілу ґрунтуються на моментах розподілу. Момент розподілу – це середня k-го ступеня відхилень x a . Залежно від величини а моменти поділяють на первинні (а = 0), центральні a x і умовні (a = const). Ступінь k визначає порядок моменту. В загальному вигляді центральний момент k-го порядку розраховується за формулою:

M k xi x k fі ,

fі

де хі – значення окремої варіанти;

x – середня арифметична; k – ступінь моменту;

fi – частота окремої варіанти.

Для того, щоб характеристика скошеності не залежала від масштабу вимірювання ознаки для порівняння ступеня асиметрії різних розподілів, використовують стандартизований момент третього ступеня. В такому разі коефіцієнт асиметрії визначається за формулою:

79

де М3 – центральний момент третього порядку;– середнє квадратичне відхилення.

Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини та називається ексцесом. Для вимірювання ексцесу використовують коефіцієнт, побудований за допомогою стандартизованого моменту четвертого порядку, який розраховується за формулою:

де М4 – центральний момент четвертого порядку.

Якщо Е = 3, то розподіл уважається нормальним, при E < 3 – плосковершинний, при E > 3 - розподіл має гостровершинну форму. Термін «ексцес» грецького походження (kurtosis), тому назви форми ексцесу походять від цього кореня слова (див. рис.6.10):

Рис.6.10. Види розподілу:

– нормальний (мезокуртичний) (Е = 3);

– гостровершинний (стрічкокуртичний) (Е > 3);

– плосковершинний (платокуртичний) (Е < 3).

Наведений графік свідчить, що для стрічкокуртичної кривої характерне розміщення більшості одиниць сукупності поблизу центра. У випадку платокуртичної кривої (форма силуету – плато) варіанти значно віддалені від центру розподілу. Помірне розміщення навколо центра розподілу варіант визначає форма ексцесу у вигляді мезокуртичної кривої. На практиці часто в одному розподілі поєднуються всі названі особливості, а саме: одновершинний розподіл може бути симетричним та гостровершинним, або плосковершинним з лівосторонньою асиметрією, або гостровершинним з правосторонньою асиметрією тощо.

80

6.5. Показники диференціації та концентрації

Процеси і явища в промисловому і сільськогосподарському виробництві, фінансовій та комерційній діяльності, демографічній, соціальній або політичній галузях, що вивчаються статистикою, як правило, характеризуються внутрішньою структурою, яка із часом може змінюватися. Динаміка структури викликає зміну внутрішнього змісту досліджуваних об’єктів і їх економічну інтерпретацію, приводить до змін встановлених причинно-наслідкових зв’язків. Тому вивчення структури і структурних зрушень займає дуже важливе місце

вкурсі статистики.

Устатистиці під структурою розуміють сукупність одиниць, яким притаманна певна стійкість внутрішньо групових зв’язків при збереженні основних ознак, що характеризують цю сукупність як ціле.

Одним із найважливіших завдань держави є забезпечення сталого соціально-економічного розвитку на основі пропорційного співвідношення між окремими підсистемами. Тому останнім часом все більше уваги приділяється питанням теорії та практики аналізу пропорційності (або нерівномірності) розподілу як одного із напрямів обґрунтування взаємозв’язків розподілів,

зокрема: ресурсів та їх використання; чисельності населення і споживання матеріальних благ і послуг; доходів і витрат; попитом і пропозицією та ін.

Практичний аналіз потребує дослідження і врахування у процесі управління пропорційності як двох взаємопов’язаних показників (результативної та факторної) ознак, так і однієї результативної оцінки з кількома факторними. За групову ознаку можуть при цьому слугувати окремі регіони, галузі, види діяльності, групи фізичних та юридичних осіб і т. ін.

Основні напрямки вивчення нерівномірності розподілу в різних соціально-економічних явищах:

оцінка структури аналізованих сукупностей з використанням квантилів розподілу для виявлення різного рівня диференціації;

визначення узагальнюючих характеристик концентрації та локалізації. Мірою оцінки розшарування сукупності слугує коефіцієнт децильної

диференціації. Коефіцієнт децильної диференціації, що є відношенням розмірів дев’ятого і першого дециля (наприклад, відношення мінімального середньодушового доходу 10% найбагатшого населення до максимального середньодушового доходу 10% найменш забезпеченого населення), дорівнює:

де D9 – дев’ятий дециль D1 – перший дециль.

Але цей показник не зовсім точно вимірює рівень диференціації, так як співставляються, наприклад, мінімальна величина активів 10% самих великих банків із максимальною величиною активів 10% самих маленьких банків. Точніше рівень диференціації можна оцінити, співставляючи середні рівні

81

активів 10% самих великих і 10% самих маленьких банків. Цей показник називають фондовим коефіцієнтом Кф.

Ступінь нерівномірності розподілу досліджуваної ознаки, не пов’язаний ні з обсягом сукупності, ні з чисельністю окремих груп, називають концентрацією. При дослідженні нерівномірності розподілу досліджуваної ознаки за територією поняття “концентрація” замінюють поняттям “локалізація”. Централізація означає зосередженість (скупченість) обсягу ознаки у окремих одиниць (наприклад, капіталу в окремих комерційних банках, продукції якогось виду на окремих підприємствах і т. ін.).

Узагальнюючий показник централізації ІZ розраховується за формулою:

де mi – значення ознаки і-ої одиниці сукупності ;

n

mi - обсяг ознаки всієї сукупності;

i 1

n - обсяг сукупності (кількість одиниць, що входять у сукупність).

Максимального значення ІZ досягає тільки за умови, що сукупність складається тільки із однієї одиниці, якій належить весь обсяг ознаки. Мінімальне значення цього показника наближається до нуля, але ніколи його не досягає.

Оцінка нерівномірності розподілу між окремими складовими сукупності ґрунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності di і обсягом значень ознаки Di.. Якщо розподіл значень ознаки рівномірний, то di = Di, а відхилення часток свідчать про певну нерівномірність, яка вимірюється коефіцієнтами локалізації та концентрації.

Особливу групу показників диференціації доходів становлять коефіцієнти концентрації доходів. Вони належать до системи оцінок, відомої як методологія Парето – Лоренца – Джині, що знайшла широке застосування в міжнародній соціальній статистиці. Італійський економіст і соціолог В. Парето (1848 – 1923) установив, що між рівнем доходів і числом їх одержувачів існує зворотна залежність, названа в літературі «законом Парето». Американський статистик і економіст О. Лоренц (1876 – 1959) розвив цей закон, запропонувавши його графічне зображення у вигляді кривої лінії, яка дістала назву «кривої Лоренца». Італійський статистик і економіст К. Джині (1884 – 1965) розробив методику розрахунку коефіцієнта концентрації доходів, названого його ім’ям.

Крива Лоренца дає графічне уявлення про ступінь нерівномірності розподілу сукупного доходу за групами населення. Рівномірний розподіл доходу це такий розподіл, коли певній частці населення відповідає точно така сама частка сукупного доходу. На графіку Лоренца, побудованого в координатах: вісь абсцис - частки населення, вісь ординат - частки доходу, лінією рівномірного доходу є діагональ квадрата. Крива лінія, побудована за фактичними показниками рівня доходу різних

82

груп населення, відбиває реальний розподіл сукупного доходу серед груп населення. Чим більше ця лінія відхиляється від діагоналі, тим більш нерівномірно розподілений дохід у суспільстві, а отже, тим вища його концентрація [13, с. 414 - 417].

Коефіцієнт локалізації визначається для кожної складової сукупності за формулою:

де di (dфак ) - частка i-ої групи розподілу за кількістю елементів сукупності (частка факторної ознаки);

Di (dрез ) - частка i-ої групи розподілу за обсягом значень ознаки (частка результативної ознаки)..

Таким чином, коефіцієнт локалізації показує відношення частки результативної ознаки до частки факторної. Якщо Li < 1, то це означає, що на і-ий регіон припадає менше результативної ознаки порівняно із пропорційною часткою факторної ознаки, і навпаки. У складі коефіцієнтів локалізації вирізняються дві групи зі значеннями Li < 1 та Li > 1, тобто із від’ємними та додатними значеннями пропорційності розподілу по конкретній групі.

Для визначення їхнього впливу на загальну концентрацію по кожній групі розраховуються суми модулів:

D –= Σ |dрез – dфак | та D + = Σ |dрез – dфак |.

Далі визначається частка цих сум у загальній сумі відхилень:

М – = D – / Σ |dрез – dфак | та М + =D + / Σ |dрез – dфак |.

Визначені показники дають характеристику ролі цих груп у формуванні як від’ємних, так і додатних характеристик розподілу та використовуються під час розроблення відповідних управлінських рішень. На основі цих характеристик розподілу досліджують і багатофакторну пропорційність, використовуючи комбіновану модель, у яку входять одна результативна ознака і сукупність факторних ознак. Це дає змогу зокрема ранжирувати факторні ознаки за мірою взаємозв’язку та впливу на розподіл результативної ознаки.

Коефіцієнт концентрації (коефіцієнт Лоренца), як відносна характеристика нерівності в розподілі доходів, є узагальнюючою для сукупності характеристикою відхилення розподілу від рівномірного і визначається за формулою:

Чим ближче значення цього показника до 1 (100%), тим вищий рівень концентрації,тобто існує повна нерівність розподілу за досліджуваною ознакою, при значенні КЛ = 0 розподіл ознаки за всіма одиницями сукупності є рівномірним. При визначенні цього коефіцієнта можна оперувати як частками

83

одиниці, так і відсотками. Порівняння структур на основі відхилень часток дозволяє вимірювати диференціацію сукупності за даними інтервальних рядів із нерівними інтервалами та атрибутивних рядів розподілу.

Найбільш відомим показником концентрації є коефіцієнт Джині, який зазвичай використовують для вимірювання диференціації або соціального розшарування. У загальному вигляді його розраховують за формулою:

де di - частка i-ої групи розподілу за кількістю елементів сукупності; Di - частка i-ої групи розподілу за обсягом значень ознаки;

Dні – накопичена частка i-ої групи розподілу за обсягом значень ознаки..

Якщо частки представлені у %, то попередню формулу можна перетворити:

для 10% розподілу –

k

G 110 0,2 Dн ;

i 1 i

для 20% розподілу –

k

G 120 0,4 Dн .

i 1 i

Коефіцієнт Джині змінюється в тих же межах, що і коефіцієнт Лоренца.

Наприклад, цей коефіцієнт може використовуватися для аналізу рівня концентрації доходів у окремих груп населення. Чим ближче значення до 1, тим вища концентрація доходів у окремих груп населення; чим ближчий він до 0, тим вищий рівень рівності в розподілі сукупного доходу суспільства.

Оцінювання інтенсивності структурних зрушень

Визначення структурних зрушень окремих частин сукупності та узагальнюючих характеристик структурних зрушень в цілому по сукупності базується на відносних показниках структури (див. лекцію до теми №4 "Узагальнюючі статистичні показники"), що являють собою співвідношення окремих частин і цілого. При цьому вони можуть бути представлені як частка (коефіцієнт) або питома вага (%). Як часткові, так і узагальнюючі показники структурних зрушень можуть відображати або “абсолютну” зміну структури у процентних пунктах чи долях одиниці, або її відносну зміну у процентах чи коефіцієнтах. “Абсолютна” зміна показана в лапках, тому що цей показник є абсолютним за методологією розрахунку, а не за суттю та одиницями виміру. До таких показників відносять:

“абсолютний” приріст питомої ваги і - ої частини сукупності;

темп зростання питомої ваги ( відносна зміна) і - ої частини сукупності;

84

середній “абсолютний” приріст питомої ваги і - ої частини сукупності;

середній темп зростання питомої ваги ( відносна зміна) і - ої частини сукупності за кілька періодів часу;

лінійний і квадратичний коефіцієнти “абсолютних” структурних зрушень;

квадратичний коефіцієнт відносних структурних зрушень;

лінійний коефіцієнт “абсолютних” структурних зрушень за n періодів

“Абсолютний” приріст питомої ваги і - ої частини сукупності показує на скільки процентних пунктів збільшилася (+) або зменшилася (-) ця структурна частина в j – ий період часу порівняно із (j – 1) періодом:

Темп зростання питомої ваги представляють у %, це завжди додатна величина. Але, якщо в сукупності мали місце якісь структурні зрушення, то частина темпів зростання буде більшою за 100%, а частина - меншою.

Якщо сукупність, що досліджується, представлена даними не за два, а за три і більше періодів, то з’являється необхідність у визначенні середніх показників структурних зрушень. Так, середній “абсолютний” приріст питомої ваги і - ої частини сукупності визначають як середню арифметичну просту із послідовно визначених абсолютних приростів за кожен період часу. При цьому слід пам'ятати, що сума середніх абсолютних приростів питомої ваги для всіх k структурних частин сукупності, так як і сума їх приростів за один часовий інтервал, завжди повинна дорівнювати нулю.

Середній темп зростання питомої ваги ( відносна зміна) і - ої частини сукупності за кілька періодів часу визначається за формулою середньої геометричної простої.

Узагальнюючими показниками структурних зрушень у випадках, коли виникає необхідність оцінити структурні зрушення у соціально-економічному явищі в цілому за якісь окремі часові періоди або у кількох структур, що належать до окремих об’єктів за один і той же часовий період, є лінійний та квадратичний коефіцієнти “абсолютних” структурних зрушень, які визначають за формулами:

85

лінійний коефіцієнт “абсолютних” структурних зрушень

де k – кількість структурних частин сукупності;

dij - питома вага (частка) і - ої частини сукупності в j – ий період часу; dij-1 - питома вага (частка) і - ої частини сукупності в (j – 1) період часу.

квадратичний коефіцієнт “абсолютних” структурних зрушень

Лінійний та квадратичний коефіцієнти “абсолютних” структурних зрушень (у процентних пунктах) дозволяють отримати зведену оцінку швидкості зміни питомої ваги окремих частин сукупності. Для зведеної характеристики інтенсивності зміни питомої ваги окремих частин сукупності використовують квадратичний коефіцієнт відносних структурних зрушень:

Цей показник відображає той середній відносний приріст питомої ваги (у відсотках), який спостерігався за період, що досліджується.

Для зведеної оцінки структурних зрушень у досліджуваній сукупності в цілому за весь часовий інтервал, що охоплює кілька тижнів, місяців, кварталів чи років, найбільш доцільно використовувати лінійний коефіцієнт

“абсолютних” структурних зрушень за n періодів (у процентних пунктах):

Цей показник може використовуватися як для порівняння динаміки двох і більше структур, так і для аналізу динаміки однієї і тієї ж структури за різні за тривалістю періоди часу.

Для забезпечення порівнянності структур одного об’єкта в динаміці іноді доводиться перегруповувати дані, тобто перегруповувати статистичні

86

матеріали, раніше зведені в групи. Це дає змогу забезпечити порівнянність структур двох сукупностей за однією й тією ж самою ознакою у часі або просторі.

Перегрупування здійснюється зменшенням або збільшенням кількості раніше утворених груп. Розрізняють два способи вторинного групування:

просте укрупнення інтервалів;

перегрупування за часткою окремих груп в загальному їх підсумку (пропорційний дольовий перерозподіл).

Якщо межі інтервалів первинного і вторинного групування збігаються, то частоти інтервалів, що об’єднуються, просто підсумовуються.

Вважається, що в межах інтервалу розподіл частот (або часток) підпорядковується рівномірному закону розподілу. Це припущення дає можливість розбивати інтервал первинного групування пропорційно співвідношенню частин ширини розбитого інтервалу і обчислювати відповідні значення частот.

За аналогією з коефіцієнтом концентрації при порівнянні структури одного об’єкта за двома ознаками або структур двох об’єктів розраховують коефіцієнт подібності (схожості) структур:

P 1 0,5 d j dk .

де dj та dk - питома вага (частка) відповідно j - ої та k - ої сукупності. Якщо структури однакові, Р = 1. Чим більші відхилення структур, тим

менше значення коефіцієнта Р.

87

Змістовий модуль 3. АНАЛІЗ ЗАКОНОМІРНОСТЕЙ ДИНАМІКИ

Тема 7. Аналіз інтенсивності динаміки

План вивчення теми

7.1.Поняття та складові елементи рядів динаміки (часових рядів). Передумови й об’єктивні умови для побудови рядів динаміки

7.2.Види рядів динаміки та їх особливості

7.3.Статистичні характеристики часових рядів: абсолютний приріст, темп зростання, темп приросту, абсолютне значення 1% приросту; їх взаємозв’язок

7.4.Середні характеристики часового ряду

7.5.Оцінка прискорення (уповільнення) розвитку. Порівняльний аналіз динамічних рядів; коефіцієнти випередження та еластичності, умови їх використання

Після вивчення теми студенти повинні:

знати: в чому полягають передумови й об’єктивні умови для побудови рядів динаміки (часових рядів); зміст статистичних характеристик (абсолютних і відносних) рядів динаміки, їх взаємозв’язок;

уміти: обґрунтовано використовувати на практиці основні статистичні характеристики (абсолютні та відносні) для аналізу інтенсивності динаміки, проводити порівняльний аналіз динамічних рядів.

Бібліографічний список: [7 – 10; 17 - 22 ]

7.1.Поняття та складові елементи рядів динаміки (часових рядів). Передумови й об’єктивні умови для побудови рядів динаміки

Суспільно-економічні явища безперервно змінюються. Протягом певного часу – місяць за місяцем, рік за роком змінюється кількість населення, обсяг та структура суспільного виробництва, рівень продуктивності праці тощо. Вивчення поступального розвитку й змін суспільних та економічних явищ – одне з основних завдань статистики.

Для кращого розуміння і аналізу зміни досліджуваних явищ у часі статистичні дані, що їх характеризують, необхідно систематизувати у хронологічному порядку і вже потім аналізувати. У статистиці це виконується за допомогою рядів динаміки або ще їх називають часовими рядами.

Отже, ряди динаміки – це ряди чисел, що характеризують закономірності зміни суспільних явищ і процесів у часі, тобто це сукупність значень статистичних показників , розташованих у хронологічному порядку.

Кожний ряд динаміки складається з двох елементів:

числових значень статистичних показників (рівнів ряду) – y;

періодів або моментів часу, яким відповідають рівні ряду – t.

88

Таким чином, під час вивчення динаміки важливі не лише числові значення рівнів, а й їх послідовність. Як правило, часові інтервали між рівнями однакові (доба, тиждень, місяць, квартал, півріччя, рік тощо). Якщо прийняти за одиницю довжину певного інтервалу, послідовність рівнів можна записати у вигляді:

у1, у2 , у3 , у4 , . . . , уn ,

де у – рівень динамічного ряду

n – кількість рівнів (довжина динамічного ряду).

Ряди динаміки дозволяють охарактеризувати розвиток явища в часі, виявити тенденції зміни, а також за цими даними побудувати прогноз на наступний період лише в тому разі, коли вони правильно побудовані.

Основними правилами побудови й аналізу рядів динаміки є:

1.Періодизація розвитку.

2.Порівнянність рівнів ряду.

3.Відповідність розміру інтервалу інтенсивності розвитку явища.

4.Підпорядкованість динамічного ряду у часі.

Періодизація розвитку означає розтин явища, яке вивчається, у часі на однорідні етапи, в межах яких показник підкоряється одному закону розвитку. По своїй суті періодизація розвитку – це типологічне групування у часі.

Порівнянність рівнів ряду повинна витримуватися за колом об’єктів, які підлягають дослідженню за територією (просторова порівнянність) за одиницями виміру за часом реєстрації за методологією розрахунків тощо.

Рівні рядів динаміки формуються в результаті зведення та групування статистичних даних, а також їх обробки за різні проміжки часу. Головне, щоб рівні характеризували дійсну зміну величини показника, а не були пов’язані із змінами їх обчислення. Важливо, щоб зміни в явищі, яке аналізується за допомогою рівнів динамічного ряду, були обумовлені природою самого явища,

ане змінами, наприклад, у методиці обчислення показників чи іншими причинами, які можуть істотно вплинути на рівень показника ряду динаміки.

Ряд динаміки об’єктивно відображає тенденцію розвитку лише за умови порівнянності між собою його рівнів. Порівнянність всіх рівнів ряду між собою є основною вимогою при побудові рядів динаміки. Порівнянність рівнів ряду повинна забезпечуватися:

за періодами часу;

за критичним моментом (для явищ із сезонними коливаннями);

за територією;

за колом охоплюваних одиниць (наприклад, зміна підпорядкованості об’єктів, відомчої приналежності);

за методологією обчислення показника (наприклад, чисельність робітників на підприємстві в одні роки визначалася на початок кожного року,

ав інші - як середньорічна чисельність);

за одиницями виміру (наприклад, за роки незалежності в Україні як грошова одиниця виміру використовувалися рублі, карбованці. купони, гривні).

Непорівнянність показників ряду динаміки може бути викликана різними причинами і умовами. Такими причинами можуть бути територіальні зміни,

89

зміни кількості підприємств, які входять до одного виробничого об’єднання, зміни одиниці виміру (наприклад, грошова реформа) тощо. Для приведення у порівнянний вигляд використовують прийом "зімкнення рядів динаміки". Його сутність полягає в об'єднанні в один ряд (більш тривалий) двох або кількох рядів динаміки, рівні яких розраховані за різними методологіями або за різними територіальними межами. Виконується це через коефіцієнти перерахунку (1 метод) або шляхом заміни абсолютних величин відносними (2 метод).

Коли рівні ряду за різні періоди часу відрізняютья методикою їх визначення, то зімкнення РД виконують, приводячи обидві їх частини до одніє методики. (Наприклад, якщо одна частина РД представлена моментним показником на початок або на кінець відповідних періодів часу, а друга – інтервальним показником у вигляді середньої величини за відповідний період часу, то для зімкненя такого РД першу частину необхідно теж визначити у вигляді середніх величин – середньорічних, середньоквартальних або середньомісячних).

Для здійснення зімкнення рядів необхідно, щоб для одного з періодів (перехідного) існували дані, які було розраховано за різними методологіями або в різних межах (умови прикладу наведені в таблиці 7.1).

1 метод – з використанням коефіцієнтів перерахунку.

Коефіцієнт - сумірник зміни обсягу реалізації продукції за рахунок збільшення кількості підприємств у складі об’єднання ”Онікс” дорівнює:

Ксум = 45 : 30 = 1,5.

Далі коригуємо дані за 1999 та 2000 роки:

Q1999 = 20 · 1,5 = 30 млн. грн.; Q2000 = 26 · 1,5 = 39 млн. грн..

Зімкнений ряд динаміки, за яким можна виконувати аналіз, наведено у таблиці 7.2.

Таблиця 7.2

Динаміка реалізації продукції об’єднанням ”Онікс”, млн. грн. (зімкнений РД із врахованим коефіцієнтом - сумірником)

90

2 метод - заміна абсолютних рівнів відносними.

За 1999р. значення буде дорівнювати 20 = 0,667;

30

Зімкнений за цим методом ряд динаміки, за яким можна виконувати аналіз, наведено у таблиці 7.3.

Таблиця 7.3

Динаміка реалізації продукції об’єднанням ”Онікс”, млн..грн. (зімкнений РД у відносних одиницях)

7.2.Види рядів динаміки та їх особливості

Економічні та соціальні явища дуже різні і тому вони можуть бути представлені у хронологічному порядку у вигляді різних рядів динаміки. Класифікація рядів динаміки за чотирма напрямками представлена на рис. 7.1.

Залежно від статистичної природи показника, який відображає рівень ряду, розрізняють динамічні ряди первинних та похідних показників, абсолютних, середніх та відносних величин.

Ряди динаміки первинних показників – це такі ряди, рівні яких характеризуються даними спостереження.

Ряди динаміки похідних показників – це такі ряди, рівні яких відображені показниками, розрахованими на основі первинних даних.

Ряди динаміки абсолютних величин – це такі ряди динаміки, в яких рівні ряду наведені у вигляді реально існуючих іменованих показників. Вони дають підсумкову характеристику розвитку явища, наприклад, кількість зареєстрованих злочинів обсяг виробленої продукції обсяг проданого товару кількість працюючих на підприємстві тощо.

Ряди динаміки відносних величин – це такі ряди динаміки, в яких всі рівні ряду наводяться у відносних величинах. Вони дають характеристику розвитку явища в їх взаємозв’язку та взаємовідносинах один з одним та виражаються у відсотках, проміле або продециміле. Ці ряди можна використовувати для аналізу структурних зрушень у розвитку явища, які інакше встановити складно. Наприклад,

вивчити зміни питомої ваги певного виду продукції на підприємстві без побудови ряду динаміки відносних величин дуже важко.

Ряди динаміки середніх величин – це такі ряди динаміки, в яких рівні ряду наведені у вигляді середніх показників. Ці ряди дають змогу дослідити зміну середніх показників у часі. Наприклад, за декілька років можна проаналізувати зміну кількості вогнепальної зброї, яка припадає на одну групу

91

злочинців, щоб охарактеризувати зміну озброєності злочинців проаналізувати середню продуктивність праці на підприємстві тощо.

Залежно від характеру явища, яке вивчається, рівні ряду динаміки можуть відноситися або до окремих проміжків часу, або до конкретної дати (моменту) часу. Відповідно до цього динамічні ряди діляться на інтервальні та моментні.

РЯДИ ДИНАМІКИ

За кількістю показників

Одномірні Багатомірні

За повнотою часу

Абсолютних величин

Рис. 7.1. Класифікація рядів динаміки

92

Рівень моментного ряду фіксує стан явища на певний момент часу t.

Наприклад, кількість робітників та службовців підприємства на 1 січня число поданих заяв від абітурієнтів до вищого навчального закладу на 5 липня курс валюти на певну дату тощо.

Відмінною особливістю моментного динамічного ряду є те, що його рівні не можна безпосередньо підсумовувати. Підсумовування рівнів моментного ряду не має сенсу, тому що окремі значення показника можуть бути присутні в декількох рівнях.

В інтервальному ряді рівень виступає як агрегований результат процесу, тобто визначає його обсяг за певний проміжок часу. Кількісне вираження рівня в цьому випадку залежить від тривалості часового інтервалу. Так, виробництво електроенергії за рік значно більше ніж за місяць обсяг продукції, виготовленої на підприємстві за тиждень, менше ніж за місяць урожай, зібраний за день, менше урожаю, зібраного протягом тижня тощо. Слід мати на увазі, що й похідні показники, які обчислюються на основі інтервальних рядів, на відміну від моментних також залежать від тривалості інтервалу часу. Так, середньодобове виробництво електроенергії на душу населення значно менше середньорічного.

Таким чином, характерною особливістю інтервальних рядів динаміки є те, що їх рівні завжди одержуються підсумовуванням рівнів за якісь проміжки часу, тобто величина рівнів інтервального ряду залежить від тривалості проміжку часу, за який обчислюються показники. Чим більший інтервал часу взято, тим більшим буде рівень динамічного ряду. За кількістю показників динамічні ряди діляться на одномірні та багатомірні.

Одномірні динамічні ряди характеризують зміну одного показника. Багатомірні динамічні ряди характеризують зміну двох і більше показників. В свою чергу, багатомірні ряди діляться на два види: паралельні ряди та ряди взаємопов’язаних показників.

За повнотою часу, який відображений у рядах динаміки, їх можна поділити на повні, неповні та накопиченим підсумком (кумулятивні).

Вповних рядах динаміки моменти або періоди часу йдуть один за одним

зрівними інтервалами часу, наприклад, кількість працюючих на перше число

кожного місяця результати фінансово-економічної діяльності підприємства на початок року тощо.

В неповних рядах динаміки така послідовність між проміжками часу не додержується. Прикладом цього може бути вивчення руху кількості працюючих (не кожен день хтось зараховується на роботу і не через якийсь певний час відраховується з роботи) або зміни кількості осіб, які відбувають покарання у вигляді позбавлення волі (вони обов’язково прибувають в місця позбавлення волі по етапу, про цей день хоча й повідомляють заздалегідь адміністрацію виправно-трудового закладу, але не через певні інтервали часу, а за потребою).

У кумулятивних рядах динаміки рівні ряду відображаються результатами розвитку явища за певний час (в органах внутрішніх справ звітність подається лише таким чином: спочатку за січень, потім за два місяці,

93

потім за три, чотири і так далі). Застосування таких рядів дає змогу одразу отримати дані за звітний період з початку року.

7.3.Статистичні характеристики часових рядів: абсолютний приріст, темп зростання, темп приросту, абсолютне значення

1% приросту; їх взаємозв’язок

Рядом динаміки є ряд послідовних рівнів, при співставленні яких між собою можна отримати характеристику швидкості та інтенсивності розвитку явища. У результаті такого порівнювання рівнів отримують систему абсолютних та відносних показників динаміки. Виконання розрахунків при цьому можливо у двох варіантах, які схематично представлені на рис. 7.2.:

o 1-й варіант - кожний рівень ряду динаміки порівнюється безпосередньо з попереднім, і таке порівняння називається порівнянням із змінною базою,

а розраховані показники –ланцюговими характеристиками динаміки.

o 2-й варіант - кожний рівень ряду динаміки порівнюється з одним і тим же попереднім рівнем, який прийнято за базу порівняння. В якості базового рівня вибирають початковий рівень ряду динаміки, або рівень, з якого починається якийсь новий етап розвитку явища. Таке порівняння називається порівнянням з постійною базою, а розраховані показники – базисними характеристиками динаміки.

Розрахунок характеристик ряду динаміки

У0

Рис. 7.2. Ланцюговий та базисний методи розрахунку характеристик ряду динаміки

де У0 – базисний рівень показника; Уt – рівень, що аналізується; Уt-1 – попередній рівень; Уn – кінцевий рівень показника.

Базисні показники характеризують кінцевий результат всіх змін у рівні ряду від періоду, до якого належить базисний рівень, до даного (і-го ) періоду.

94

Ланцюгові показники характеризують інтенсивність зміни рівня від періоду до періоду (або від дати до дати) в межах проміжку часу, що вивчається.

Абсолютний приріст (зменшення) t - це показник ряду динаміки, який характеризує на скільки одиниць змінився поточний рівень показника порівняно з рівнем попереднього або базового періоду. Абсолютний приріст із змінною базою виражає абсолютну швидкість зміни рівнів ряду динаміки. Розраховується абсолютний приріст як різниця двох рівнів динамічного ряду:

Коефіцієнт зростання - це показник ряду динаміки, який показує:

у скільки разів зріс поточний (порівнюваний) рівень показника, що аналізується, порівняно з рівнем попереднього (базового) періоду – якщо значення коефіцієнту зростання Кt > 1;

яку частку становить поточний (порівнюваний) рівень показника до рівня попереднього (базового) періоду періоду – якщо значення коефіцієнту зростання Кt < 1;

що ніяких змін не відбулося - якщо значення коефіцієнту зростання Кt =1.

Коефіцієнт зростання Кt розраховується як відношення рівнів ряду і

Зв’язок між ланцюговими і базисними коефіцієнтами зростання полягає в тому, що добуток ланцюгових коефіцієнтів зростання дорівнює кінцевому базисному:

Темп зростання – це коефіцієнт зростання, але представлений у відсотках, тобто

Тр = Кt ∙ 100,

або для ланцюгових Тр = (yt / y t—1)·100,

для базисних Тр = (yt / y0)·100.

Темп приросту - це показник ряду динаміки, який показує на скільки відсотків змінився поточний (порівнюваний) рівень аналізованого показника

95

порівняно з рівнем попереднього або базового періоду. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання.

Для ланцюгових характеристик:

Тпр = 100 · t / y t—1 = 100 (yt – yt—1 ) / y t—1 = 100 (Кt – 1) = Тр - 100.

Аналогічно взаємопов’язані і базисні темпи приросту.

Абсолютне значення одного відсотка приросту — це відношення абсолютного приросту до відповідного темпу приросту або одна сота попереднього рівня. Абсолютне значення 1 % приросту показує, чого вартий 1% і розраховується як співвідношення абсолютного приросту й темпу приросту. Алгебраїчно це співвідношення дорівнює 0,01 рівня, взятого за базу порівняння:

А% = t / Тпр =( yt - y t—1)/ 100 (yt - yt—1)/ yt--1 = yt--1 / 100 = 0,01 yt—1.

Для базисних темпів приросту значення А% однакові, тому їх не розраховують.

7.4.Середні характеристики часового ряду

Середній рівень динамічного ряду - середня, обчислена на основі рівнів динамічного ряду. Особливості розрахунку залежать від виду ряду динаміки, він визначається як середня арифметична проста (якщо рівні ряду представлені інтервальними абсолютними величинами), середня арифметична зважена (якщо рівні ряду представлені моментними величинами із нерівними періодами часу між моментами) або середня хронологічна (якщо рівні ряду представлені моментними величинами із рівними періодами часу між моментами).

Середній або середньорічний абсолютний приріст - це показник ряду динаміки, який показує на скільки одиниць у середньому за одиницю часу (щорічно) за певний період змінювався рівень показника, що аналізується. Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів:

де m = n - 1 - число ланцюгових абсолютних приростів, n – число періодів (моментів) у ряду динаміки.

Середній або середньорічний темп зростання - це показник ряду динаміки, який показує скільки відсотків у середньому за одиницю часу (щорічно) за певний період становить зміна рівня показника, що аналізується.

Середній або середньорічний темп приросту - це показник ряду динаміки,

який показує на скільки відсотків у середньому за одиницю часу (щорічно) за певний період змінювався рівень показника, що аналізується. Ці показники краще розраховувати після визначення середнього або середньорічного коефіцієнта зростання (росту).

96

Середній коефіцієнт зростання розраховують за формулою середньої геометричної:

7.5.Оцінка прискорення (уповільнення) розвитку. Порівняльний аналіз динамічних рядів; коефіцієнти випередження та

еластичності, умови їх використання

Якщо абсолютна та відносна швидкість динаміки у межах періоду, що вивчається, неоднакова, порівнянням однойменних характеристик за різні інтервали часу вимірюється прискорення (уповільнення) динаміки.

Різниця абсолютних ланцюгових приростів ' = t - t--1 характеризує

абсолютне прискорення (+) чи уповільнення (-) динаміки.

Відносне прискорення — це відношення абсолютного прискорення до абсолютного приросту, прийнятого за базу ( Δ' / іб ) або це темп приросту абсолютного приросту. Розраховується тільки у випадку, якщо абсолютний приріст, прийнятий за базу порівняння, додатне число. Якщо інтервали часу неоднакові, використовують середні абсолютні прирости відповідних інтервалів.

При порівнюванні розвитку двох явищ використовують показники, що являють співвідношення базисних темпів зростання або темпів приросту за однакові відрізки часу за двома рядами динаміки. Ці показники називають

коефіцієнтами випередження:

За допомогою цих показників порівнюють ряди динаміки, що мають однаковий зміст, але належать до різних територій або об’єктів, а також ряди динаміки різного змісту, що характеризують один і той же об’єкт.

Якщо ряди динаміки взаємопов’язані, тобто рівні їх являють собою фактор х та результат у, із співвідношення темпів приросту цих ознак визначають, на скільки відсотків змінюється результативна ознака у зі зміною факторної ознаки х на 1 %. За економічним змістом співвідношення темпів приросту є коефіцієнтом еластичності :

Кел = Тпр у / Тпр х.

Під час аналізу статистичних характеристик неповних рядів динаміки слід пам’ятати про зв’язок, що існує між базисними та ланцюговими абсолютними приростами та коефіцієнтами росту. Цей взаємозв’язок допомагає визначити характеристики за відсутні у ряді динаміки проміжки часу.

97

 Тема 8. Виявлення і вимірювання тенденцій розвитку

План вивчення теми

8.1.Основні компоненти часових рядів. Основні методи виявлення та аналізу тенденцій розвитку

8.2.Рівняння тренду, етапи визначення та обґрунтування найпридатнішого функціонального виду, суть параметрів

8.3.Екстраполяція трендів як один із методів прогнозування рівнів соціально-економічних явищ

Після вивчення теми студенти повинні:

знати: принципи виявлення та аналізу тенденції розвитку, екстраполяції трендів як методу прогнозування рівнів соціально-економічних явищ;

уміти: обґрунтовано використовувати на практиці основні методи виявлення та аналізу тенденцій розвитку, прогнозувати розвиток шляхом екстраполяції тренду.

Бібліографічний список: [7 – 10; 17 - 22 ]

8.1. Основні компоненти часових рядів. Основні методи виявлення та аналізу тенденцій розвитку

Рівні ряду динаміки формуються під загальним впливом великої кількості факторів, дія яких може бути тривалою або короткочасною, вони можуть бути постійно діючими і випадковими, які з’являються під впливом різних обставин. Визначення основної закономірності зміни рівнів ряду у часі потребує її кількісного вираження, більш менш вільного від дії випадкових чинників.

Основна тенденція розвитку явища – це певний напрям його зміни, який характеризується детермінованою складовою ряду динаміки. Але крім впливу основних факторів, які і визначають конкретний вид невипадкової компоненти (тренд), на рівні ряду впливають випадкові фактори, що викликають відхилення фактичних значень рівнів ряду від тренда.

Рівень динамічного ряду можна представити функцією:

yt f (t) (t) ,

де f(t) – тенденція, зумовлена впливом постійно діючих факторів (тренд); ε(t) – величина, що визначає вплив випадкових коливань.

Однак, існує багато явищ, яким, крім вище названих, притаманні ще й так звані сезонні коливання. Рівень таких явищ рік у рік у певні місяці підвищується, а в інші – знижується. Наприклад, витрати палива у веснянолітні місяці значно більші, ніж у осінньо-зимові; виробництво та споживання напоїв або морозива має періодичний характер; перевезення пасажирів автомобільним чи залізничним транспортом; споживання електроенергії

98

у різні години доби, дні тижня, місяці року і т. ін.. Таким чином, компонентами динамічного ряду є тенденції (тренди), випадкові та, можливо, сезонні коливання.

Маючи справу із показниками ряду динаміки дослідник завжди намагається виявити головну закономірність розвитку явища в окремі проміжки часу. Це зводиться до виявлення головної тенденції, звільненої від дії різних випадкових факторів. З цією метою ряди динаміки піддають певній статистичній обробці, яка може бути елементарно простою, або більш складною, із застосуванням математичних методів. Завдання щодо їх використання зводиться до елімінування дії випадкових, другорядних причин, а також встановлення характеру дії основних причин, що визначають динаміку досліджуваного явища.

В деяких випадках тенденцію можна встановити за значеннями рівнів ряду динаміки. Наприклад, якщо рівні постійно збільшуються, чи зменшуються. Основні тенденції – зростання чи зниження – можна поділити за їх характером. Характер основної тенденції має певне графічне зображення

(див. рис. 8.1 – 8.3).

у

t

Рис. 8.1. Рівномірний характер основної тенденції: рівномірне зростання рівномірне зниження.

Характер основної тенденції можна також встановити за допомогою абсолютних ланцюгових приростів. Якщо абсолютні ланцюгові прирости мають додатні значення, динамічний ряд має тенденцію до зростання. Якщо абсолютні ланцюгові прирости мають від’ємні значення, динамічний ряд має тенденцію до зниження. Якщо абсолютні ланцюгові прирости мають однакові значення, то характер тенденції рівномірний (рівномірне зростання чи рівномірне зниження). Якщо кожен наступний ланцюговий приріст більше за попередній, то тенденція має прискорений характер. Якщо кожен наступний ланцюговий приріст менше за попередній, то тенденція має уповільнений характер.

99

Рис. 8.2. Прискорений характер основної тенденції: прискорене зростання прискорене зниження.

Рис. 8.3. Уповільнений характер основної тенденції: уповільнене зростання уповільнене зниження.

У разі, коли рівні динамічного ряду коливаються, то наочно виявити тенденцію розвитку явища не можна. Тоді для виявлення основної тенденції розвитку застосовують методи згладжування динамічного ряду або аналітичне вирівнювання ряду динаміки.

До найбільш простих методів згладжування динамічних рядів належать методи ступінчастої середньої та плинної середньої. Метод ступінчастої середньої (укрупнення інтервалів) полягає в тому, що рівні первинного динамічного ряду поєднуються в збільшені інтервали і розраховуються середні в кожному зі створених інтервалів.

Наприклад, утворюється новий динамічний ряд, в якому окремі інтервали

– це об’єднання трьох інтервалів первинного динамічного ряду. В такому разі середня кожного укрупненого інтервалу розраховується так:

100

у1 = (у1 + у2 + у3) : 3

у2 = (у4 + у5 + у6) : 3

у 3 = (у7 + у8 + у9) : 3 і т. д.

Суть методу середньої плинної полягає в тому, що середні обчислюються також за збільшеними інтервалами, але на відміну від попереднього методу здійснюється послідовне пересування меж збільшених інтервалів на один первинний інтервал до кінця динамічного ряду. У такому разі середні інтервалів розраховуються за формулами:

у1 = (у1 + у2 + у3) : 3

у2 = (у2 + у3 + у4) : 3

у 3 = (у3 + у4 + у5) : 3 і т. д.

Якщо значення рівнів похідного (згладженого) динамічного ряду не дають можливості встановити чітку тенденцію, проводять нове згладжування, при цьому беруть ще більші інтервали. Слід зауважити, що для об’єднання беруться інтервали первинного динамічного ряду. Згладжування повторюють доти, доки не виявиться чітка тенденція, або коли не залишиться три укрупнених інтервали, оскільки подальше згладжування вже не має сенсу. Через дві точки завжди можна провести лінію, але при цьому можна отримати результат, протилежний реальному стану.

8.2. Рівняння тренду, етапи визначення та обґрунтування найпридатнішого функціонального виду, суть параметрів

Якщо згладжування ряду динаміки не дає можливості виявити тенденцію розвитку або її характер, то відповідь на це питання можна напевне одержати за допомогою аналітичного вирівнювання заданого (вихідного) динамічного ряду методом найменших квадратів.

Метод аналітичного вирівнювання дає змогу не лише виявити тенденцію розвитку, а й кількісно виміряти її.

Під аналітичним вирівнюванням ряду динаміки у статистиці розуміють побудову функції Y = f(t), яка аналітично виражає залежність значень ознаки Y від часу t. Такі функції, а також їх графіки називають трендовими кривими. За допомогою трендової кривої завжди можна виявити основну тенденцію розвитку явища, що вивчається, а також її характер.

Процес побудови трендової кривої складається з двох етапів:

вибір виду функції f(t)

обчислення параметрів функції f(t).

Вид функції f(t) можна встановити візуально за кореляційним полем з урахуванням економічної (фізичної тощо) суті явища, що вивчається.

Кореляційне поле (див. рис. 8.4) являє собою координатну площину tOy із зображеними на ній точками з координатами (ti, yi).

101

де у – середній рівень динамічного ряду.

Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t = 0) обрати центральний інтервал. Із використанням спрощеного методу із введенням нумерації періодів часу від умовного нуля значення умовних періодів t залежать від того, парну чи непарну кількість рівнів має динамічний ряд.

Якщо число рівнів парне (наприклад, 6), умовні періоди мають значення, наведені в табл. 8.1.

Таблиця 8.1

Значення параметра t у разі введення умовного нуля для парної кількості рівнів динамічного ряду

Якщо число рівнів непарне (наприклад 7), умовні періоди мають значення, наведені в табл. 8.2.

Оскільки мета введення умовного нуля – максимальне спрощення розрахунків, то відстані між сусідніми рівнями динамічного ряду з умовними періодами мають бути мінімальними, проте однаковими впродовж усього ряду. Таким чином, у разі парної кількості рівнів динамічного ряду відстані між будьякими двома рівнями з умовними періодами дорівнюють двом; у разі непарної кількості рівнів динамічного ряду відстані між будь-якими двома рівнями з умовними періодами дорівнюють одиниці. Умовні періоди, розташовані ліворуч умовного нуля, набувають від’ємних значень, а ті, що розташовані праворуч – додатних.

Таблиця8.2

Значення параметра t у разі введення умовного нуля для непарної кількості рівнів динамічного ряду

Незалежно від кількості рівнів у динамічному ряді з умовними періодамиt = 0, а тому система нормальних рівнянь для лінійної моделі тренду матиме такий вигляд:

103

Тоді параметри а0 та а1 для лінійної моделі тренду розраховуються за формулами:

Якщо у трендовій моделі використовуються нелінійні функції, то вони приводяться до лінійного вигляду за допомогою певних математичних перетворень. Так, степенева функція призводиться до лінійного вигляду за допомогою логарифмування, гіпербола – заміною змінної.

8.3.Екстраполяція трендів як один із методів прогнозування рівнів

соціально-економічних явищ

Зробити прогноз явища у означає обчислити значення ознаки Y на той майбутній період часу t, який нас цікавить. Очевидно, що будь-який прогноз може бути тільки наближеним і може вважатись реальним тільки за умови збереження у майбутньому тенденції розвитку явища та її характеру. Метод прогнозування на періоди за межами ряду динаміки (на майбутнє або за минулі періоди часу) називають екстраполяцією. Метод прогнозування на періоди пропущених періодів часу в середині ряду динаміки називають інтерполяцією.

Точковий прогноз здійснюється за допомогою екстраполяції трендової моделі, тобто прогнозоване значення явища обчислюється за встановленою формулою. При цьому слід мати на увазі той факт, що рівняння трендової кривої побудоване з використанням умовних періодів, а тому для визначення точкового прогнозу вводиться наступний період. Наприклад, якщо динамічний ряд містить шість періодів, то точкова оцінка розраховується для наступного, сьомого періоду (див. табл. 9.1) якщо динамічний ряд містить сім періодів, то точкова оцінка розраховується для наступного (умовного) четвертого періоду

(див. табл. 9.2).

Інтервальний прогноз являє собою інтервал значень ознаки у, який із заданою ймовірністю покриває (або має покривати) справжнє значення:

y y t t S Yt ,

де уt – точковий прогноз

t – довірче число, яке обирається з таблиць розподілу Стьюдента (якщо кількість рівнів динамічного ряду менше 30) або з таблиць нормального розподілу (якщо кількість рівнів динамічного ряду більша за 30)

SYt – залишкове середнє квадратичне відхилення.

Залишкове середнє квадратичне відхилення розраховується за формулою:

104

 Тема 9. Індексний метод

План вивчення теми

9.1.Суть індексів і їх роль в аналізі соціально-економічних явищ. Класифікація індексів

9.2.Індивідуальні індекси

9.3.Методологічні принципи побудови зведених індексів; агрегатні та середньозважені індекси

9.4.Індексний метод економічного аналізу кількісного впливу чинників на наслідок

9.5.Дослідження динаміки середніх величин індексним методом: індекси середніх величин змінного складу, фіксованого складу і структурних зрушень; їх взаємозв’язок

Після вивчення теми студенти повинні:

знати: сутність і функції індексів; методологічні принципи побудови зведених індексів, умови використання індексів агрегатної форми та середньозважених індексів; системи взаємопов’язаних зведених індексів та індексів середніх величин;

уміти: обґрунтовано використовувати на практиці різні види та системи взаємопов’язаних індексів для аналізу динаміки складних соціальноекономічних явищ; оцінювати абсолютні та відносні ефекти впливу чинників на динаміку індексованих показників.

Бібліографічний список: [7 – 10; 17 - 22 ]

9.1.Суть індексів і їх роль в аналізі соціально-економічних явищ.

Класифікація індексів Індекс - це узагальнюючий відносний показник, що характеризує зміну рівня

будь-якого явища чи процесу в часі, просторі чи порівняно з планом, нормою, стандартом. Індекси найчастіше використовують під час аналізу динаміки складних економічних явищ, які можуть бути представлені певними групами неоднорідних елементів, кількісні характеристики яких безпосередньо не піддаються додаванню.

Як відносна величина індекс подається у формі коефіцієнта або процента (якщо одержану величину коефіцієнта помножити на 100 %). Назва індексу відбиває його соціально-економічний зміст, а числове значення – інтенсивність зміни або ступінь відхилення (від норми, плану, стандарту).

Індекси застосовують для порівняльної характеристики сукупності в часі, для порівняння фактичного рівня з планом, для порівняння рівнів виробництва продукції, цін, продуктивності праці в різних регіонах, на різних підприємствах, для різних товарів. Їх застосовують для оцінки ролі окремих факторів у зміні складних подій та явищ, динаміки середніх показників, зміна яких залежить від структурних зрушень. За допомогою індексу, вираженого у процентах, можна визначити на скільки відсотків змінилося досліджуване явище. Крім того, за допомогою індексу можна визначити не лише відносні зміни, а й абсолютні зміни як явища в цілому (наприклад, зміни товарообігу), так і зміни явища під впливом факторів. Так, зведений індекс цін

106