Тема 4. Подання статистичних даних: таблиці та графіки

План вивчення теми

4.1.Статистичні таблиці як метод наочного подання статистичних даних. Елементи статистичної таблиці. Види статистичних таблиць і правила їх побудови

4.2.Статистичні графіки, їх роль в аналізі соціально-економічних явищ.

Класифікація статистичних графіків. Основні елементи статистичних графіків і правила їх побудови

4.3. Побудова графіків з використанням «Мастера диаграмм» в середовищі EXCEL

Після вивчення теми студенти повинні:

знати: основні види та правила побудови статистичних таблиць; види та аналітичні функції статистичних графіків; правила побудови графіків і діаграм у середовищі Excel;

вміти: правильно складати статистичні таблиці; правильно обирати види та засоби побудови статистичних графіків та діаграм для максимальної відповідності між змістом і логічною природою статистичних даних і їх наочним представленням, у тому числі з використанням «Мастера диаграмм» в середовищі Excel.

Бібліографічний список: [7 – 10; 12; 17; 18 - 22 ]

4.1.Статистичні таблиці як метод наочного подання статистичних даних. Елементи статистичної таблиці. Види статистичних таблиць і правила їх побудови

Невід’ємним елементом зведення та групування є статистична таблиця. За логічним змістом статистична таблиця розглядається як “статистичне речення”, тому вона має підмет та присудок.

Підмет – це об’єкт дослідження: перелік елементів сукупності, їх групи, окремі територіальні одиниці або часові інтервали. Як правило, підмет розміщують у лівій частині таблиці у назві рядків, але не обов’язково, все залежить від наявної інформації та зручності розташування.

Присудок таблиці – це система показників, що характеризують підмет як об’єкт дослідження. Як правило, присудок формує в логічній послідовності верхні заголовки таблиці. Залежно від характеру інформації розробка присудка може бути простою чи складною. Проста розробка присудка передбачає паралельне розміщення показників, складна – комбіноване.

Як присудок таблиці, так і її підмет можуть мати різну розробку: просту, групову чи комбінаційну. Залежно від розробки підмета таблиця також може бути простою (простий перелік одиниць сукупності, підмет не ділиться на групи), груповою (групування одиниць за однією ознакою, підмет ділиться на групи за однією ознакою) та комбінаційною (підмет ділиться на групи за декількома ознаками). Розробка присудка на вид таблиці не впливає.

39

Нижче наведено загальну схему статистичної таблиці, її макет.

Таблиця 4.1

Назва таблиці (загальний заголовок)

Залежно від мети дослідження таблиці бувають типологічними, структурними та аналітичними. Існують і інші критерії класифікації статистичних таблиць. Приклади побудови різних видів таблиць наведені в табл. 4.2 – 4.5.

Таблиця 4.3

Розподіл промислових підприємств України за формами власності, 1995 р.

40

Таблиця 4.4

Розподіл працівників ВАТ „Захід” за рівнем заробітної плати

Таблиця 4.5

Розподіл робітників ЗАТ „Схід” за рівнем кваліфікації

Статистична таблиця, як засіб наочного і компактного подання статистичних даних, має бути правильно оформлена для легкого та однозначного сприйняття наведеної в ній інформації. Тому існують певні правила складання та оформлення статистичних таблиць, дотримання яких робить таблиці основним засобом подання узагальненої інформації щодо стану і розвитку масових соціально-економічних явищ і процесів.

Використовуючи статистичні таблиці, необхідно дотримуватись певних правил їх оформлення:

статистична таблиця повинна мати назву, в якій зазначається об’єкт, його часова і географічна ознаки

назва таблиці, заголовки рядків і граф мають бути чіткими, лаконічними і без скорочень

таблиця має містити лише ту інформацію, яка безпосередньо характеризує об’єкт дослідження. Слід уникати зайвої, другорядної інформації

у верхніх і бічних заголовках указують одиниці вимірювання з використанням загальноприйнятих скорочень (т, кВт, грн. тощо). Якщо

41

одиниця вимірювання спільна для всіх даних таблиці, її зазначають над таблицею після назви

рядки та графи доцільно нумерувати. У заголовках граф можна наводити розрахункові формули або надавати методику розрахунку, наприклад:

гр. 4 = гр. 2 + гр. 3

інформація, що міститься у рядках та графах таблиці, узагальнюється підсумковим рядком “Разом”, який завершує статистичну таблицю

числові дані однієї графи мають бути наведені з однаковою точністю

якщо таблиця займає декілька сторінок, то на наступних аркушах перед таблицею праворуч пишеться “Продовження таблиці”, а на останньому – “Закінчення таблиці”. При цьому заголовки граф наводяться, якщо таблиця займає багато сторінок, якщо дві–три сторінки, можна просто нумерувати

графи

статистична таблиця не повинна містити порожніх клітинок, тому відсутність даних у таблиці позначається відповідно до причин:

а) якщо клітинка не може бути заповнена (частіше за все це підсумкова клітинка, коли показники відповідної графи не підсумовуються), проставляється знак “Х”; б) відсутність самого явища позначається через тире “–”;

в) відсутність відомостей про явище позначається трьома крапками “...”, або скорочені слова “н.від.”; г) числа, величина яких менша прийнятої для даної графи точності позначаються 0,0 або 0,00

якщо потрібна додаткова інформація, певні уточнення цифрових

даних, до таблиці додається примітка: якщо примітка одна, то посилання на неї позначається знаком “*)”, який проставляється в правому верхньому куті клітинки; якщо приміток багато, то посилання на них позначаються відповідною цифрою з дужкою розташованими у правому верхньому куті відповідної клітинки, при цьому посилання йдуть в порядку зростання цифри;

усі таблиці мають бути пронумеровані, номер зазначається перед заголовком таблиці, при цьому знак “№” не пишуть.

4.2.Статистичні графіки, їх роль в аналізі соціально-економічних явищ. Класифікація статистичних графіків. Основні елементи статистичних графіків і правила їх побудови

Крім таблиць важливим способом подання інформації про соціальноекономічні явища є їх графічне зображення. Графіки мають певну перевагу перед текстовим викладом і статистичними таблицями, оскільки не тільки за допомогою графічних засобів унаочнюють статистичні дані, а й істотно полегшують і прискорюють сприйняття та розуміння їх. Для вивчення і побудови статистичних графіків важливе значення має їх класифікація. Вона допомагає зрозуміти відмінності між різними видами графіків, з'ясувати їх можливості щодо розв'язування завдань статистичного дослідження.

42

Графіки, які використовують для зображення статистичних даних, дуже різноманітні. Вони класифікуються залежно від обраного критерію:

-за загальним призначенням виділяють аналітичні, ілюстративні та інформаційні графіки;

-за функціонально-цільовим призначенням виділяють графіки групувань, рядів розподілу, рядів динаміки, графіки взаємозв’язку і графіки порівнянь:

-за видом поля виділяють діаграми, картограми та картодіаграми. У статистиці найбільш поширені діаграми, тому термін діаграма часто ототожнюють з терміном статистичний графік;

-за графічним образом виділяють крапкові, лінійні, площинні, просторові, фігурні (стовпчикові, стрічкові, квадратні, кругові, секторні) діаграми. Діаграми – це вид графіків, в яких цифровим (кількісним) даним відповідають різні фігури і лінії.

Статистичний графік – це умовне відображення числових величин та їх співвідношень за допомогою геометричних фігур, ліній та інших графічних засобів з метою узагальнення й аналізу статистичної інформації.

Статистичні графіки стають інструментом дослідження масових суспільних явищ завдяки таким властивостям як наочність, синоптичність (можливість охопити одним поглядом усю сукупність наведених статистичних даних), сугестивність (можливість пояснити особливості статистичної сукупності, які перебувають у прихованому стані). Ці властивості складають основу пізнавальності та аналітичності статистичних графіків. Саме завдяки цим властивостям статистичні графіки є важливим засобом узагальнення та аналізу статистичних даних, а іноді єдиним і незамінним знаряддям дослідження, наприклад при виявленні форми зв’язку між явищами.

Кожен графік складається з графічного образу та допоміжних елементів.

Графічний образ – це сукупність точок, ліній, фігур та їх різних комбінацій, за допомогою яких зображуються статистичні дані.

До допоміжних елементів графіка належать: поле, просторові та масштабні орієнтири, експлікація.

Поле графіка – це той простір, в якому розташовуються геометричні та інші графічні знаки, що зображують графік. Поле графіка характеризується його форматом, тобто розміром та пропорціями.

Просторові орієнтири визначають розташування геометричних чи інших графічних знаків, порядок їх розміщення у полі графіка. Цей порядок обумовлюється характером та особливостями статистичних даних, завданням аналізу, метою дослідження і задається певною системою координат.

Система координат – це сукупність елементів, які визначають положення точки у просторі. При побудові статистичних графіків використовують прямокутну (декартову), полярну та трикутну (тригональну) системи координат.

Прямокутна система координат використовується найчастіше завдяки її простоті. Вона утворюється двома перпендикулярними прямими лініями:

43

горизонтальна лінія – вісь абсцис, вертикальна – вісь ординат. Точка перетину створює початок координат. Напрям праворуч і вгору вважається додатним ліворуч і вниз – від’ємним.

Полярна система координат будується навколо певної точки, яка називається полюсом або центром обертання і позначається через О вона розміщена на прямій лінії, що називається полярною віссю.

Масштабні орієнтири надають графічним знакам кількісну визначеність, тобто вказують на їх розміри.

Масштаб – це умовна міра переведення числового значення статистичної величини у графічну, і навпаки. Масштаб, як правило, виражають довжиною відрізка, прийнятого за одиницю статистичної величини, що відображається на графіку. Якщо масштаб побудований у вигляді площ або об’ємів, масштабами є відповідні одиниці площі чи об’єму. Масштаб має бути обраний таким чином, щоб статистичні дані вмістилися на полі графіка, і водночас не втрачалися відмінності та особливості статистичних даних, щоб їх порівнянність була наочною.

Масштаб відображається на графіку за допомогою масштабної шкали – лінії, поділеної відповідно до обраного масштабу, – яка складається з трьох елементів:

лінії, яка є носієм шкали, і співпадає з віссю координат

поділок, або позначок шкали – це риски або точки, розміщені в певному порядку на лінії шкали

числових позначень, які відповідають поділкам шкали і визначають розміри показників чи явищ, відображених на графіку.

Залежно від наявної інформації масштабна шкала може бути як рівномірною, так і нерівномірною.

Експлікація графіка є досить важливим та необхідним елементом будьякого графіка і складається зі словесних пояснень, без яких узагалі неможливо його зрозуміти. До експлікації належать такі елементи:

загальний заголовок, що має чітко й стисло розкривати основний зміст графіка і давати характеристику місця та часу, яких стосуються зображувані статистичні дані

підписи вздовж масштабних шкал, які відтворюють розміри показників чи явищ та одиниці їх виміру. Числові позначення на горизонтальну шкалу (вісь абсцис) наносяться під нею, зліва направо в порядку зростання, а на вертикальну шкалу – ліворуч від неї вгору, також у порядку зростання

пояснювальні написи повинні розкривати зміст окремих елементів графічного образу. Вони можуть міститися на самому графіку у вигляді ярликів (при цьому написи мають бути короткими і точними та розміщуватися так, щоб було цілком зрозуміло, до якого елемента вони належать) або у вигляді легенди – спеціально винесених за межі графічного образу умовних позначень. Легенду застосовувати особливо доцільно, коли її можна використати для кількох графіків.

Для побудови стовпчикової діаграми ознаку розташовують за віссю абсцис, а її кількісне вираження – за віссю ординат для побудови стрічкової

44

діаграми – навпаки: ознаку розташовують за віссю ординат, а її кількісне вираження – за віссю абсцис. При цьому графік зображується у вигляді смужки певної довжини, що розташовується вертикально – стовпчикова діаграма (див. рис. 5.2) або горизонтально – стрічкова діаграма (див. рис. 5.3). На цих видах діаграм окремі смужки можуть розташовуватися з певними проміжками, як правило, рівними або без проміжків. У цьому разі стовпчикова діаграма набуває вигляду гістограми.

Рис. 5.2. Кількість злочинів за їх видами у регіоні за рік:

1 – злочини проти життя та здоров’я особи 2 – злочини проти власності 3 – злочини у сфері господарської діяльності 4 – злочини проти громадської безпеки 5 – злочини у сфері службової діяльності.

0 10 20 30 40 50

Кількість злочинів

Рис. 5.3. Кількість злочинів за їх видами у регіоні за рік:

1 – злочини проти життя та здоров’я особи 2 – злочини проти власності 3 – злочини у сфері господарської діяльності 4 – злочини проти громадської безпеки 5 – злочини у сфері службової діяльності.

Якщо ознаку та її кількісне вираження зобразити у вигляді крапок, що послідовно поєднані лініями, отримуємо лінійну діаграму (див. рис. 5.4). При цьому розташування ознаки та її кількісного вираження обирається довільно за певним логічним міркуванням.

45

За допомогою стовпчикової, стрічкової чи лінійної діаграм можна зобразити співвідношення різних явищ, тобто ці види діаграм використовуються для порівняння абсолютних, відносних або середніх величин.

Рис. 5.4. Кількість злочинів за їх видами у регіоні за рік:

1 – злочини проти життя та здоров’я особи 2 – злочини проти власності 3 – злочини у сфері господарської діяльності 4 – злочини проти громадської безпеки 5 – злочини у сфері службової діяльності.

Графічне зображення структури явищ і структурних зрушень

Для статистичного дослідження складу сукупності використовують структурні діаграми. Структурні діаграми – це діаграми питомих ваг, що характеризують відношення окремих частин сукупності в їх загальному обсязі. Зрозуміло, що сума складових ваг дорівнюватиме одиниці у разі визначення відносних величин структури як коефіцієнти, або 100 % у разі визначення відносних величин структури у відсотках.

Кругові (секторні) діаграми (див. рис. 5.5), що відображають структуру того чи іншого явища, набули найбільш широкого застосування. При цьому дуги секторів пропорційні значенням відповідних часток. Секторні діаграми зображуються у вигляді кола, яке поділене на відповідні сектори. На полі сектора позначається частка у відсотках. Якщо число не вміщується на полі сектора, його проставляють поруч за межами кола. Поле сектора заштриховується або фарбується різними кольорами. Під час побудови секторних діаграм існують певні правила: найбільший за величиною сектор має найсвітліший колір або зовсім лишається чистим (не заштрихованим), а найменший сектор має найщільніше штрихування чи найтемніший колір. Поруч з колом мають бути наведені клітинки з відповідними позначеннями, які розташовуються в певній логічній послідовності (в порядку зростання або зменшення ознаки).

46

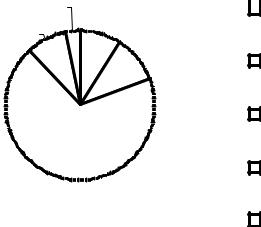
Секторні діаграми зберігають наочність і простоту сприймання в тих випадках, коли сукупність має не більше 5 – 6 складових частин, чисельність яких помітно відрізняється.

Обсяг і структуру явища можна зобразити також стовпчиковою або стрічковою діаграмою. При цьому, наприклад, стовпчик розбивають на частини відповідно до структури сукупності. Кожна частина відповідно заштриховується або замальовується окремим кольором. Іноді для характеристики структури сукупності використовують кругові і квадратні діаграми.

Рис. 5.5. Структура злочинів за їх видами у регіоні В за перше півріччя

Графіки порівняння статистичних величин

Для порівняння статистичних даних можна використовувати стовпчикові та стрічкові діаграми, коли порівнювальні величини відрізняються не дуже суттєво одна від одної.

Коли порівнювальні показники відрізняються один від одного в багато разів, застосування стовпчикових або стрічкових діаграм стає недоречним. У такому разі використовуються площинні діаграми, до яких належать квадратні (див. рис. 5.6) або кругові (див. рис. 5.7). У цьому випадку площа фігур, що застосовуються в діаграмах, має бути пропорційною відображуваним величинам.

Рис. 5.6. Чисельність населення Китаю й Канади за 1982 рік, млн. чол.

47

В наведеному прикладі основою прямокутника є середня заробітна плата працівників фірми, висотою – кількість працюючих, площа прямокутників – відповідний фонд заробітної плати.

4.3.Побудова графіків з використанням «Мастера диаграмм» в середовищі EXCEL

Значно полегшує і прискорює процес побудови різних статистичних графіків технологія автоматизованого опрацювання статистичної інформації засобами одного із найпопулярніших пакетів прикладних програм – Microsoft Excel 2000 (надалі – Excel). Засоби Ехсеl дають змогу просто і швидко будувати різні типи графіків. Технологія побудови окремих типів графіків засобами Ехсеl докладно розглянута у [ 9 ]. Особливості методологій і технології автоматизованої побудови статистичних графіків засобами Ехсеl полягають у тому, що терміни і поняття, які використовуються для позначення основних елементів статистичних графіків в Ехсеl, не завжди збігаються з традиційно вживаними в економікостатистичній літературі.

В Ехсеl замість поняття «поле діаграми» застосовуються такі нові поняття, як область побудови діаграми і область діаграми. Область побудови діаграми - це область, до якої входять лише координатні осі і сама діаграма, а область діаграми - це область, яка включає крім координатних осей і самої діаграми ще й заголовок діаграми, позначення одиниць вимірювання координатних осей, легенду тощо.

Кожний елемент діаграми можна виділити, активізувати, а потім здійснювати з ним різні перетворення, як-от: змінювати розміри, редагувати, здійснювати форматування (оформлення). З переміщенням курсора миші по побудованій діаграмі біля кожного елемента діаграми з'являється підказування щодо його назви. Ці підказування допомагають знайти потрібний елемент діаграми, який можна виділити, активізувати за допомогою лівої кнопки миші.

Виділення будь-якого елемента діаграми можна зробити також за допомогою панелі інструментів Диаграммы. Щоб відобразити цю панель інструментів на екрані, потрібно обрати команду Вид, Панели инструментов, а

49

потім у списку, що з'явився, - елемент Диаграмма або із контекстного меню вибрати команду Диаграмма і далі будувати необхідний графік.

Ехсеl дає можливість змінювати зовнішній вигляд області побудови діаграми та області діаграми, тобто змінювати форму ліній рамки обрамлення, колір і візерунок заповнення їхніх внутрішніх частин. Для зміни ліній рамок, обрамлення кольорів і візерунків області побудови діаграми й області діаграми необхідно відкрити відповідне діалогове вікно Формат области построения і Формат области диаграммы.

ВЕхсеl замість терміна графічний образ використовується термін маркер даних

-один елемент даних, або, за статистичною термінологією, цей термін відповідає такому вигляду графічного образу, як точка, за допомогою якої на графіках відображають окремі значення певної ознаки кожного елемента статистичної сукупності або певних груп її елементів, а поняття ряд даних відповідає поняттю статистичних рядів - рядів розподілу і часових рядів. При побудові діаграм на основі даних, наведених у таблиці, окремими рядами даних можуть бути дані або одного стовпчика, або одного рядка таблиці.

Для позначення координатних осей - осі X і осі Y - нарівні з цими термінами в Ехсеl вводяться відповідно такі нові поняття, як Ось категорий (Вісь категорій) і Ось значений (Вісь значень). За замовчуванням Ехсеl задає шкалу таким чином, що максимальне числове значення вихідних даних є дещо меншим за максимальне числове позначення, наведене на шкалі. Про те шкалу можна задати і вручну.

Ехсеl пропонує автоматизовану побудову 14 різних типів діаграм (в Ехсеl замість терміна «графік» використовується термін «діаграма», за своїм змістом ці терміни є тотожними), причому для кожного типу діаграми є кілька видів (форматів), як площинних, так і об'ємних, які можуть бути застосовані до даного типу діаграми і які висвітлюються на екрані після вибору того чи іншого типу і виду діаграми.

Важливою особливістю програми Ехсеl є те, що вона дає змогу просто і швидко зробити перегляд кожного типу як стандартних, так і нестандартних діаграм безпосередньо на екрані дисплея після введення вихідних даних. Цей перегляд здійснюється за допомогою графічного зображення обраного типу і виду діаграми, яке виникає перед очима після вибору того чи іншого типу і виду діаграми та натискання і утримання командної кнопки Просмотр результата, що міститься в нижній частині діалогового вікна Тип диаграммы. Щоб відчинити це діалогове вікно, потрібно обрати команду Вставка, Диаграмма. Такий перегляд надає можливість не лише перевірити правильність вибору конкретного типу і виду діаграми, а й просто і швидко обрати такий її тип і вид, який найкраще відповідатиме характеру і цілям графічного зображення вихідних статистичних даних.

Представимо основні типи діаграм, що їх пропонує будувати Ехсеl, при цьому їх перелік наводитимемо в тому самому порядку і з тим самим їх описом, які містить діалогове вікно Тип диаграммы. Опис кожного типу діаграм, який містить діалогове вікно Тип диаграммы, братимемо в лапки, доповнюючи його певними коментарями.

1.ГИСТОГРАММА (Стовпчикова) - «відображає значення різних категорій», тобто значень, розміщених на осі X. Маркерами (графічними образами) в гістограмі

євертикальні прямокутники (стовпчики), які можуть бути розміщені залежно від виду діаграми або суміжно, тобто щільно прилеглими один до одного, або роздільно,

50

тобто з певним проміжком між сусідніми прямокутниками. Вживаний у російськомовній версії Ехсеl для позначення цього типу діаграм термін «гистограмма» не можна визнати вдалим, оскільки він не відображає специфічних особливостей графічного образу цього типу діаграм.

У англомовній версії Ехсеl для позначення цього типу діаграм використовується слово «Соlитп», що означає «стовпчик». Термін «гістограма» в економіко-статистичній літературі є загальноприйнятим для позначення специфічного виду діаграм, який застосовується для графічного зображення особливого виду статистичних рядів, а саме інтервальних рядів розподілу.

2. ЛИНЕЙЧАТАЯ (Стрічкова) - «відбиває значення різних категорій». Зауважимо, що в цьому типі діаграм на відміну від стовпчиків маркерами (графічним образом) є горизонтальні прямокутники (стовпчики), які в економікостатистичній літературі заведено позначати терміном стрічками або смугами, а саму діаграму називати стрічковою або смуговою. У англомовній версії Ехсеl для позначення цього типу діаграм використовується слово «Ваr», що означає стрічка.

3.ГРАФИК (Графік) - «графік з маркерами, які позначають точки даних», точніше кажучи, це лінійний графік з позначеннями окремих значень статистичного ряду, що відбивається на графіку. У лінійному графіку маркерами (графічними образами) є зазвичай суцільна лінія.

4.КРУГОВАЯ (Кругова) - «відбиває внесок кожного значення в загальну суму». Маркерами в круговій діаграмі є окремі сектори круга. Цю діаграму дуже часто використовують для представлення структури сукупності.

5. ТОЧЕЧНАЯ (Точкова) - «дає можливість порівнювати пари значень». У точковій діаграмі маркерами (графічним образом) є точки, які в окремих видах діаграм цього типу з'єднуються відрізками ліній одна з одною.

6.С ОБЛАСТЯМИ (Шарові) - «відбиває зміну як загальної суми, так і внеску окремих значень». В економіко-статистичній літературі діаграми такого типу називаються шаровими.

7.КОЛЬЦЕВАЯ (Кільцева) - «подібна до кругової, але може відбивати кілька рядів даних».

8.ЛЕПЕСТКОВАЯ (Радіальна) - «діаграма з маркерами, які позначають значення даних».

9.ПОВЕРХНОСТЬ (Поверхня) - «відбиває зміну значень за двома вимірами у вигляді поверхні».

10.ПУЗЬІРЬКОВАЯ (Бульбашкова) - «відбиває на поверхні набори даних із трьох значень. Подібна до точкової діаграми, але третя величина відбиває розмір бульбашки».

11.БИРЖЕВАЯ (Біржова) - «відбиває набори даних із трьох значень (найвищий курс, найнижчий та курс закриття)».

12.ЦИЛИНДРИЧЕСКАЯ (Циліндрична) - «гістограма зі стовпчиками у вигляді циліндрів».

13.КОНИЧЕСКАЯ (Конусова) - «гістограма зі стовпчиками у вигляді

конусів».

14.ПИРАМИДАЛЬНАЯ (Пірамідальна) - «гістограма зі стовпчиками у вигляді пірамід».

51

Як уже зазначалося, вказані в діалоговому вікні Тип диаграммы типи діаграм, не зовсім збігаються з аналогічними назвами і характеристиками, вживаними в економіко-статистичній літературі. Ці зауваження стосуються і наведеної для кожного типу діаграм характеристики щодо їх призначення. Крім того, вони не охоплюють усіх видів статистичних графіків, зокрема, одностовпчикову і однострічкову діаграми, серійні та компонентні діаграми, двобічну стрічкову діаграму, діаграми в трикутній системі координат тощо.

Вказані типи діаграм називаються стандартними. Крім цих типів діаграм Ехсеl пропонує ще 19 нестандартних типів. Нестандартні типи діаграм базуються на стандартних типах, проте вони містять додаткові графічні засоби, які розширюють не лише наочні, а й пізнавальні, аналітичні можливості діаграм. Зокрема, вони містять такі графічні елементи, як легенда, координатна сітка, логарифмічна шкала, пояснювальні написи, різні кольори для заливки тощо. Щоб мати доступ до нестандартних типів діаграм, потрібно обрати команду Вставка, Диаграмма і після появи діалогового вікна Тип диаграммы - вкладку Нестандартные.

Графічні засоби Excel дають можливість будувати діаграми двох видів залежно від місця їх розташування та особливостей побудови, зберігання та редагування. Як вбудовані діаграми, так і діаграми на діаграмних сторінках можуть бути побудовані такими способами: автоматично, тобто за замовчуванням; за допомогою майстра діаграм і перебудовою раніше побудованих діаграм. Однак у будь-якому випадку, перед тим, як розпочати побудову будь-якої діаграми, вихідна таблиця даних, на основі яких треба побудувати діаграму, повинна бути готова і виділена, активізована.

Автоматичний спосіб побудови діаграм або за замовчуванням є

найпростішим і найшвидшим способом їх створення. Він дає змогу створювати діаграми, так би мовити, миттєво. Але автоматично побудована діаграма не містить деяких основних елементів експлікації діаграми, зокрема заголовка діаграми, написів на вертикальній шкалі (осі ординат) і т. ін. Однак графічні засоби Ехсеl дозволяють усіх їх додати, включаючи і таблицю вихідних даних, а також здійснювати різні види форматування, наприклад форматування тексту і чисел, осей і маркерів даних тощо.

Майстер діаграм є одним із найпотужніших графічних засобів Ехсеl. Майстер діаграм складається з чотирьох послідовних діалогових вікон, що дозволяють управляти процесом побудови діаграми і контролювати його шляхом перегляду на кожному кроці її побудови. Це діалогове вікно містить кнопки, за допомогою яких можна переходити від одного діалогового вікна, виконуючи за допомогою його засобів певний набір процедур з побудови діаграми, до іншого, або пропускати те або інше діалогове вікно для автоматичного завершення побудови діаграми.

Перед тим, як розпочати побудову діаграми за допомогою майстра діаграм, вихідна таблиця даних, на основі котрої треба побудувати діаграму, повинна бути готова і виділена. Майстер діаграм дозволяє зробити це в процесі побудови діаграми, але попереднє виділення спрощує процес її побудови.

52

Змістовий модуль 2. АГРЕГУВАННЯ ІНФОРМАЦІЇ ТА АНАЛІЗ ЗАКОНОМІРНОСТЕЙ РОЗПОДІЛУ

Тема 5. Узагальнюючі статистичні показники

План вивчення теми

5.1.Сутність статистичних показників, їх функції та види

5.2.Абсолютні статистичні величини, особливості представлення їх видів

5.3.Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання

5.4.Середні величини у статистиці, їх види, умови наукового застосування та особливості обчислення

Після вивчення теми студенти повинні:

знати: суть і види узагальнюючих статистичних показників; принципи, які забезпечують відповідність використання відповідних показників

іметодів їх визначення реальним соціально-економічним явищам і процесам;

вміти: правильно розраховувати різні статистичні показники у відповідності з сутністю досліджуваних явищ і процесів та метою статистичного дослідження.

Бібліографічний список: [7 – 10; 17 - 22 ]

5.1. Сутність статистичних показників, їх функції та види

При вивченні різних соціальних і економічних явищ статистика у своїх висновках спирається на числові дані, отримані в конкретних умовах місця і часу. Статистичний показник – це кількісна характеристика соціально-економічних явищ та процесів в умовах їх якісного визначення, тобто це міра якісного і кількісного відображення певної властивості соціально-економічного явища чи процесу. Якісний зміст показника визначається суттю явища і виявляється у його назві (наприклад, чисельність населення, народжуваність, рентабельність тощо), кількісна характеристика представлена числом і одиницею виміру.

Конкретний статистичний показник характеризує розмір, обсяг явища чи процесу, що вивчається, у конкретному місці й у певний час. Показниккатегорія відображає суть, загальні відмінні властивості конкретних статистичних показників одного й того ж виду без зазначення часу, простору та кількісного значення. Система статистичних показників — це сукупність взаємопов'язаних показників, що має однорівневу чи багаторівневу структуру; має на меті розв'язання конкретного статистичного завдання. Це ієрархічна структура, на нижньому щаблі якої - узагальнюючий інтегральний показник, на верхньому - рівновагомі ознаки, які безпосередньо вимірюються. Класифікація видів статистичних показників за різними ознаками представлена на рис. 5.1.

53

Достовірність статистичних даних залежить від адекватності статистичного показника та точності й повноти вимірювання.

ВИДИ ПОКАЗНИКІВ

Рис. 5.1. Класифікація показників

54

Адекватність – це здатність показника відобразити саме ту властивість об’єкта, що передбачена програмою дослідження. Адже для однієї й тієї самої категорії можна побудувати кілька показників. Наприклад, рентабельність виробництва можна оцінити за такими показниками: балансовий прибуток, нетто-прибуток, відносно капіталу, відносно активів. Щоб показник відповідав своєму призначенню та виконував покладені на нього функції, на стадії проектування проводиться його логічне та статистичне обґрунтування. Логічне обґрунтування передбачає всебічний теоретичний аналіз абстрактних економічних категорій, наприклад, норма прибутку, продуктивність праці, рентабельність виробництва тощо. Статистичне обґрунтування передбачає розробку методології та методику кількісного вимірювання цих категорій.

Точність та повнота вимірювання залежить від статистичної структури показника, організації спостереження та обробки даних, можливостей технічних засобів. Наприклад, імпорт нафти вимірюється тоннами, а продаж пального автолюбителям – літрами зібраний урожай оцінюється центнерами, а продаж сільськогосподарської продукції населенню – кілограмами. Щоб показник відповідав своєму призначенню й виконував покладені на нього функції, необхідно логічно обґрунтувати його модель ще на етапі розробки програми статистичного спостереження.

За аналітичною функцією показників вирізняють абсолютні, відносні та середні величини. Одні характеризують масштаби явищ, другі – співвідношення між явищами, треті – поширеність явищ чи інтенсивність їх розвитку. Так як соціально-економічні явища надзвичайно складні й багатогранні, найчастіше немає можливості схарактеризувати їх якимось одним показником, тільки в їх комплексі виникає можливість дати різнобічну характеристику явища чи процесу.

5.2. Абсолютні статистичні величини, особливості представлення їх видів

Абсолютний показник - це показник у формі абсолютної величини, яка відображає фізичні властивості, часові та вартісні характеристики соціальноекономічних явищ та процесів. Абсолютні величини – це початковий вид узагальнюючих показників, які характеризують масштаб, розмір соціальноекономічного явища, його чинників на певний момент або за певний проміжок часу. Абсолютні величини являють собою іменовані числа та характеризують: 1) обсяги сукупностей, що вивчаються (наприклад, кількість студентів,

кількість навчальних закладів,кількість підприємств); 2) обсяг значень ознаки (наприклад, дохід або прибуток підприємств, обсяг виробленої продукції, заробітна плата робітників тощо).

Засоби отримання:

•реєстрація фактів;

•групування та зведення;

•розрахунок за визначеною методологією.

Одиниці вимірювання:

55

натуральні вимірники: т, кг, м, км, одиниці, особи та ін., у тому числі:

-комбіновані натуральні вимірники: т-км, кВт-год, та ін.;

-умовно-натуральні вимірники (перерахунок виконується за допомогою спеціальних коефіцієнтів - сумірників);

трудові вимірники: людино-година, людино-день;

вартісні вимірники: грн., дол. США, євро та ін.

Наприклад:

-Назва показника – обсяг продукції, що вироблена за місяць.

-Одиниця виміру – штуки, тони, метри, літри, квадратні або кубічні метри, гривні.

Індивідуальні абсолютні показники - показники, які отримують безпосередньо в процесі статистичного спостереження як результат вимірювання, зважування, підрахунку та оцінки досліджуваної кількісної ознаки щодо окремої одиниці сукупності.

Загальні об'ємні показники - це абсолютні показники, які характеризують обсяг ознаки або обсяг сукупності як у цілому щодо об'єкта, який вивчається, так

іщодо будь-якої його частини (групові); ці показники отримують шляхом зведення та групування індивідуальних абсолютних показників.

Перерахунок абсолютних величин в умовні одиниці виміру:

Якщо виникає потреба звести воєдино кілька різновидів однієї споживчої властивості, обсяги такого явища виражають в умовно-натуральних одиницях. Перерахунок в умовні одиниці здійснюють за допомогою спеціальних коефіцієнтів-сумірників, розрахованих як відношення споживчих властивостей окремих різновидів продукції до еталонних значень. Наприклад, різні види палива

переводяться в умовне паливо із теплотою згорання 29,3 мДж/кг; консерви різного об’єму – в умовні консервні банки об’ємом 353, 4 см3 і т.д.

Багато абсолютних величин подається у формі балансу. Це може бути: представлення матеріальних чи фінансових балансів за джерелами формування

інапрямами використання; баланс руху матеріальних чи фінансових ресурсів протягом якогось періоду (місяця, квартала, року).

5.3. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання

Відносний показник - показник у формі відносної величини - це результат порівняння одного абсолютного показника з іншим; характеризує співвідношення між кількісними характеристиками процесів і явищ, що вивчаються, чи міру кількісного співвідношення різнойменних чи однойменних показників.

При розрахунках відносних величин порівнювана величина - це величина, що знаходиться в чисельнику дробу; база порівняння - це величина, що знаходиться у знаменнику дробу, тобто це показник, з яким проводиться порівняння. Якщо при розрахунку структури в цілому ми не отримуємо 1 чи 100%, то необхідно здійснити коригування структури. При аналізі структури в динаміці використовується показник структурних зрушень у відсоткових пунктах.

56

Відсотковий пункт визначається як різниця між часткою і-ї складової сукупності поточного року й відповідною часткою тієї самої складової минулого року. Слід зауважити, що при цьому структури явища за поточний і попередній роки мають бути порівнянними, тобто відображати однакову кількість складових в однакових межах.

Форми вираження відносних величин:

•коефіцієнт: база порівняння = 1 (точність розрахунку - 0,000);

•відсоток: база порівняння = 100 % (точність розрахунку - 0,0);

• проміле: база порівняння = 1000 (точність розрахунку - 0);

відносні показники інтенсивності є іменованими величинами.

Використовують сім видів відносних величин, характеристика яких і методика обчислення наведені у таблиці 5.1.

57

5.4. Середні величини у статистиці, їх види, умови наукового застосування та особливості обчислення

Однією з узагальнюючих характеристик в аналізі суспільних явищ є середня величина. Статистичні середні відображують об'єктивну наявність певних умов, які проявляються в кожній одиниці досліджуваної сукупності. Середня узагальнює весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. У ній нівелюються випадкові відхилення, властиві індивідуальним значенням ознаки, яка вивчається, а також відображаються загальні умови, що формують досліджувану сукупність.

Порівняти ж між собою окремі сукупності за якоюсь конкретною ознакою можна за середнім її значенням, визначеним для кожної сукупності. Це можливо тому, що в середній величині відображається те типове, що характерне для всієї сукупності.

58

Розраховуючи конкретну середню, завжди доцільно опиратись на її логічну формулу (математичне вираження середньої), яка є відношенням обсягу ознаки до обсягу сукупності. Критерій правильного вибору форми середньої величини - це запис логічної формули розрахунку.

СЕРЕДНІ ВЕЛИЧИНИ

це узагальнююча міра варіативної ознаки у статистичній сукупності;

це узагальнюючий показник, який характеризує типовий рівень ознаки, що варіює, в розрахунку на одиницю сукупності.

Умови наукового використання середніх величин:

якісна однорідність сукупності;

сукупність має бути достатньо великою;

використання загальних середніх із груповими.

Призначення середніх в економічному аналізі:

характеристика рівня масових суспільних явищ; проведення порівняльного аналізу; вивчення тенденцій розвитку явищ; вибіркове спостереження;

вимірювання взаємозв'язків.

Для кожної середньої є лише одне правильне співвідношення, для реалізації якого залежно від даних, що існують, можна використовувати різні форми середніх: середню арифметичну, середню гармонічну, середню квадратичну, середню геометричну за не згрупованими (просту) і за згрупованими даними (зважену).

Однак в усіх випадках, коли характер величини, за якою розраховується середня, передбачає наявність ваги, неможливо замість зважених формул середніх використовувати прості, тобто незважені,

формули. Використання кожного виду середніх залежить від двох обставин, по-перше, від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні). По-друге, від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, степень, квадратичний корінь).

Середня арифметична – використовується для усереднення прямих значень ознак шляхом їх підсумовування. Якщо дані не згруповані:

x xi , n

де xi - варіанти, тобто значення ознаки, що осереднюється для i- ої одиниці сукупності;

59

n – число одиниць у сукупності.

За формулою середньої арифметичної простої обчислюються також середні у хронологічному ряді, якщо інтервали часу, за який подаються значення ознак, рівні. Якщо у хронологічному ряді наведені моментні показники, то для обчислення середньої вони замінюються півсумами значень на початок і кінець періоду. Якщо моментів більше двох і інтервали між ними рівні, то середня обчислюється за формулою середньої хронологічної:

x1 xn x2 x3 xn 1

x 2

n 1

де n– число моментів.

Якщо дані згруповані, то використовують середню арифметичну зважену, яку розраховують за формулою:

Середня гармонічна використовується для осереднення обернених індивідуальних значень ознак шляхом їх підсумовування. Для не згрупованих даних це середня гармонічна проста

Якщо дані згруповані, то використовують середню гармонічну зважену

60

Очевидно, що середню гармонічну зважену доцільно використовувати, коли відсутня інформація про значення знаменника логічної формули, тобто відсутні ваги у явному виді.

Середня геометрична визначається як добуток відносних величин динаміки xi , які є кратним співвідношенням i -го значення показника до попереднього (i -1). Формула середньої геометричної простої

де - символ добутку;

n - кількість величин, середня яких обчислюється.

Якщо часові інтервали неоднакові, використовують середню

геометричну зважену

де n ni - часовий інтервал.

У інтервальних рядах, припускаючи рівномірний розподіл у межах i -го інтервалу, як варіант xi використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою ж, як і сусіднього закритого інтервалу.

Середня арифметична – один із найбільш поширених видів середньої величини. Для більшості соціально-економічних явищ характерна адитивність, тобто можливість підсумовування обсягів сукупності, що вивчається. Наприклад, виробництво певного виду продукції, витрати палива, продаж товару тощо. Таким чином, середня арифметична застосовується у тих випадках, коли обсяг варіативної ознаки для всієї сукупності являє суму індивідуальних значень її окремих елементів. За первинними, незгрупованими даними обчислюється середня арифметична проста.

У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи за відповідними варіантами, а обсяг значень ознаки визначити як суму добутків варіант на відповідні їм частоти. Такий процес множення в статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами

– вагами. Сама назва “ваги” відображує факт різновагомості окремих варіант. У такому випадку значення ознаки осереднюється за формулою середньої арифметичної зваженої.

Для інтервального варіаційного ряду середню арифметичну обчислюють за формулою:

61

fi – частота відповідного інтервалу.

У статистиці використовується припущення, що в межах інтервалу варіанти підпорядковуються рівномірному закону розподілу. Це припущення дає можливість під час розрахунку середньої арифметичної використовувати середини інтервалів. Звичайно, при цьому розрахунок середньої набуває дещо умовного характеру, оскільки у разі відхилення від рівномірного розподілу середня інтервального ряду є менш точною, ніж середня, яка обчислена на основі первинних даних. Середнє значення інтервалу розраховується за формулою:

де х і min – нижня межа інтервалу х і max – верхня межа інтервалу.

Для визначення середини відкритого інтервалу приймають припущення, що ширина відкритого інтервалу дорівнює ширині сусіднього інтервалу. Таким чином, немає проблем з визначенням верхньої межі останнього інтервалу. Проте під час визначення нижньої межі першого інтервалу, крім загальної рекомендації, слід ураховувати якісну сутність ознаки, середня якої обчислюється. Наприклад, якщо за загальними рекомендаціями при визначенні нижньої межі отримується від’ємне значення ознаки, варто проаналізувати, чи може ця ознака мати від’ємне значення. Якщо так, нижню межу визначають за загальними рекомендаціями. Якщо ні, за нижню межу обирають нульове значення ознаки.

Середня арифметична має певні математичні властивості. Математичні властивості середньої арифметичної:

1. Алгебраїчна сума відхилень кожної варіанти від середньої арифметичної дорівнює нулю. Математично це записується таким чином:

(х і – x ) = 0.

2. Якщо кожну варіанту збільшити або зменшити на будь-яке постійне число А, то середня арифметична відповідно збільшиться або зменшиться на те

жсаме число А. У математичному записі це має вигляд:

( x A) f

x A . (5.15)

f i

3.Якщо кожну варіанту збільшити або зменшити в одну й ту саму

кількість разів А, то середня арифметична відповідно зміниться в стільки ж разів. i i

62

Уформалізованому вигляді це записується рівнянням:

( x i A) f i x A .

f i

4.Якщо частоту кожної варіанти збільшити або зменшити в одне й те саме число разів, то середня арифметична не зміниться. Математично це записується

увигляді формули:

x i ( f i A) x .

( f i A)

5.Сума квадратів відхилень кожної варіанти від середньої арифметичної прямує до мінімуму. Ця властивість записується у вигляді формули:

(х і – x ) 2 = min.

Остання властивість середньої арифметичної покладена в основу методу найменших квадратів, який широко використовується під час встановлення взаємозв’язку між явищами та розробки прогнозів.

63