
Математика для економістів Ден.. 2010 ч
.1.pdf
Неперервна функція в замкнутій і обмеженій області D досягає принаймні один раз найбільшого значення і один раз найменшого.
Похідні і диференціали функцій багатьох змінних
Означення. Нехай в деякій області задана функція z=f(x,y). Візьмемо довільну точку М(х,у) і задамо приріст х до змінної х. Тоді величина
xz=f(x+ x,y)–f(x,y) називається частинним приростом функції по х.
Можна записати
|
|
|
|
|
|
|
|
|
|
|
x z |
|
f (x x, y) f (x, y) |
. |
||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тоді |
lim |
x z |
|
називається частинною похідною функції z=f(x,y) по х. |
||||||||||||
x |
||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Позначення: |
|
z |
; z |
|
; |
f (x, y) |
; f |
|
(x, y). |
|
||||||
|
|
x |
|
x |
|
|||||||||||
|
|
|
|
|
x |
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогічно визначається частинна похідна функції по у.
z |
lim |
f (x, y |
y) f (x, y) |
. |
y |
|
|
||
y 0 |
y |
|||
|
|
|
||
Правило. Для обчислення частинних похідних користуються звичайними формулами диференціювання. Щоб знайти частинну похідну функції за однією зі змінних, потрібно решту змінних вважати сталими.
Геометричним змістом частинної похідної (припустимо xz ) є тангенс кута
нахилу дотичної, проведеної в точці N0(x0,y0,z0) до перерізу поверхні площиною
у=у0.
Повний приріст і повний диференціал
Означення. Для функції f(x,y) вираз z=f(x+ x,y+ y)–f(x,y) називається
повним приростом.
Якщо функція f(x,y) має неперервні частинні похідні, то
z f (x |
x, y |
y) f (x, y) f (x, y |
y) f (x, y |
y) |
f (x |
x, y |
y) f (x, y |
y) |
f (x, y  y)
y)  f (x, y)
f (x, y)
Застосуємо теорему Лагранжа до виразу в квадратних дужках:

|
|
|
f (x, y |
|
y) f (x, y) |
y |
|
f (x, y) |
, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
f (x |
x, y |
|
y) |
|
f (x, y |
|
|
|
y) |
|
x |
|
f (x, y |
y) |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
де y ( y, y |
y); |
x (x, x |
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тоді отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
z |
|
x |
|
f (x, y |
y) |
y |
|
f (x, y) |
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||
Так як частинні похідні неперервні, то можна записати рівності: |
|||||||||||||||||||||||||||||
|
|
|
|
|
lim |
|
f (x, y |
y) |
|
|
f (x, y) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f (x, y) |
|
|
|
f (x, y) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Означення. Вираз |
z |
|
f (x, y) |
x |
|
f (x, y) |
|
y |
|
|
|
|
x |
2 y називається повним |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||
|
|
x |
|
|
|
|
y |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
приростом функції f(x,y) в деякій точці (х,у), де |
1 і |
2 – нескінченно малі функції |
|||||||||||||||||||||||||||
при х 0 і |
у |
0 відповідно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Означення. Повним диференціалом функції z=f(x,y) називається головна |
|||||||||||||||||||||||||||||
лінійна відносно |
х і у приростів функції z в точці (х,у): |
|
|
||||||||||||||||||||||||||
dz  f x (x, y)dx
f x (x, y)dx  f y (x, y)dy
f y (x, y)dy
Для функції довільної кількості змінних:
df (x, y, z,..., t) |
f |
dx |
f |
dy ... |
f |
dt . |
|
x |
y |
t |
|||||
|
|
|
|
Наближене обчислення за допомогою повного диференціала
Нехай функція f(x,y) диференційована в точці (х,у). Знайдемо повний приріст цієї функції:
z  f (x
f (x  x, y
x, y  y)
y)  f (x, y) f (x
f (x, y) f (x 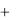 x, y
x, y  y)
y) 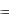 f (x, y)
f (x, y)  z
z
Якщо підставити в цю формулу вираз
z dz |
f |
x |
f |
y , |
|
|
|
||||
x |
y |
||||
|
|
|

то отримаємо наближену формулу:
f (x |
x, y |
y) f (x, y) |
f (x, y) |
x |
f (x, y) |
y . |
|
|
|
||||||
x |
y |
||||||
|
|
|
|
|
Розглянемо приклад функції багатьох змінних. Функція Кобба-Дугласа – виробнича функція, яка показує обсяг випуску продукції Y при витратах капіталу
K і трудових ресурсах L . Для випадку двох змінних вона має вигляд
|
Y AK L1 , |
|
де A - параметр |
продуктивності конкретно взятої технології, 0 |
1 - частка |
капіталу в доході. |
|
|
Приклади
1. Знайти частинні похідні функції по кожній змінній:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
ln tg |
|
x |
y . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
z |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
sin 2 |
x y |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
|
tg |
|
x |
y |
|
|
cos2 |
x |
y |
|
2 |
|
x |
|
|
y |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
sin 2 x |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Знайти повний диференціал функції u |
|
|
x y 2 z . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
u |
dx |
|
|
|
|
u |
dy |
|
|
u |
dz |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
2 |
|
|
|
|
|
u |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 zx y |
z 1 ; |
|
|
|
|
|
|
|
|
x y |
z ln x 2 yz; |
|
|
|
|
x y |
z ln x y 2 ; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
z |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
y 2 zx y2 z |
1dx |
|
|
|
|
2x y2 z yz ln xdy |
|
y 2 x y2 z ln xdz |
|
|
||||||||||||||||||||||||||||
|
|
|
3. Знайти повний диференціал функції z |
|
|
|
|
y |
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2 |
|
|
y 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
2 yx |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x (x2 |
|
|
y 2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
y (x2 |
|
|
y 2 ) y( 2 y) |
|
|
|
|
x2 |
y 2 |
2 y 2 |
|
|
|
x2 |
y 2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
(x2 |
|
y 2 )2 |
|
|
|
|
|
|
|
|
|
|
|
(x2 |
|
|
y 2 )2 |
|
|
(x2 |
y 2 )2 |
|||||||||||||||||||
dz |
|
|
2xy |
|
dx |
|
x2 |
|
y 2 |
|
dy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(x2 |
|
y 2 ) |
(x2 |
y 2 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Обчислити |
наближено |
|
значення |
|
1,041,99 |
|
ln1,02 , виходячи із значення |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функції u |
x y |
ln z |
при x = 1, y = 2, z = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Розв'язок. Із заданого виразу визначимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
x = 1,04 – 1 = 0,04, |
|
y = 1,99 – 2 = -0,01, |
z = 1,02 – 1 = 0,02. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Знайдемо значення функції u(x, y, z) = |
12 |
|
|
ln1 |
1 |
|
|
|
|
|
|
||||||||||||||||||||||||
Знаходимо частинні похідні: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
y |
x y 1 |
|
|
|
|
2 1 |
|
|
1 |
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x y |
|
|
|
ln z |
2 1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
x y ln x |
0 , |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x y |
ln z |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
y |
ln z |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Повний диференціал функції u дорівнює: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
du 0,04 |
u |
|
0,01 |
|
u |
|
0,02 |
u |
|
1 0,04 |
0 |
0,01 |
|
1 |
0,02 |
|
0,04 0,01 0,05. |
||||||||||||||||||
x |
|
y |
z |
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

 1,041,99 ln1,02 u(1,2,1) du 1 0,05 1,05
1,041,99 ln1,02 u(1,2,1) du 1 0,05 1,05
Точне значення цього виразу: 1,049275225687319176.
Завдання
1. Визначити та зобразити на рисунку область визначення функції:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
|
|||||
В.1 z |
|
x2 |
y2 |
4 |
|
|
|
|
|
16 x2 |
y2 |
|
В.2 z |
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
9 |
|
|
|
16 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В.3 |
|
z |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
В.4 |
z |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
x |
y |
x y |
|
||||||||||||||||
|
|
1 |
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В.5 |
|
z ln x |
ln y |
|
|
|
|
|
|
|
|
|
|
В.6 |
z |
|
x |
|
y |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ex |
y |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2. Знайти частинні похідні другого порядку функції: |
|
|
|
|||||||||||||||||||||||||||||
В.1. |
z |
sin( x |
|
cos y ) |
|
|
В.2 |
z |
|
1 |
ln( x2 |
|
y2 ) |
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В.3. |
z |
ln( e y cos x |
|
|
e |
y sin x ) |
В.4. |
z |
ln(tg(x y)) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В.5. |
z |
yex 2 |
y 2 |
|
|
|
|
|
|
|
|
В.6. |
z |
|
cos( x |
|
y ) |
|
|
|
|
x3 |
2 . |
|
||||||||||

Питання для самоконтролю
18.Що називається функцією багатьох змінних?
19.Що називається областю визначення функції багатьох змінних та який її геометричний зміст?
20.Що являє собою графік функції z = f(x, y)?
21.Дати означення неперервної функції трьох змінних, n змінних.
22. Що називається границею функції z = f(M) M M0?
23.Дати означення неперервної функції двох змінних у точці та на множині точок.
24.Що називається замкненою обмеженою областю?
25.Сформулювати властивості функції z = f(x, y), неперервної у замкненій обмеженій області.
26.Дати означення частинної похідної функції двох змінних по одній з них.
З‟ясувати її геометричний зміст.
27.Дати означення повного диференціала функції двох змінних та вказати формулу для його знаходження. Узагальнити цю формулу для функції n
змінних.
28.Як застосовується повний диференціал функції для наближеного обчислення її значень?
Література [1,2,4]
ПРАКТИЧНЕ ЗАНЯТТЯ № 15
Тема 10. Диференційованість функцій багатьох змінних
Мета заняття. Вивчення теми надасть студентам можливість знати методологію обчислення похідної складної та заданої неявно функції, похідної за напрямом. Також вивчити поняття градієнту функції та його властивості, поверхні та лінії рівня, зокрема, поняття лінії та поверхні байдужості в економічній теорії споживання.

План заняття
1.Похідна складної та заданої неявно функції.
2.Градієнт, властивості градієнта.
3.Похідна за напрямом.
4.Лінії рівня. Поверхні рівня.
5.Лінії та поверхні байдужості в економічній теорії.
Методичні рекомендації до практичного заняття
Похідна складної функції
1. Випадок однієї незалежної змінної. Якщо z  f (x, y) є диференційованою функцією аргументів x і y , які в свою чергу є диференційованими функціями незалежної змінної t :
f (x, y) є диференційованою функцією аргументів x і y , які в свою чергу є диференційованими функціями незалежної змінної t :
|
|
x |
|
|
(t) , |
y (t) , |
||||
то похідна складної функції z f ( (t), |
(t)) може бути обчислена за формулою |
|||||||||
|
dz |
z dx |
z |
|
dy |
. |
||||
|
|
|
|
|
|
|
|
|
||
|
dt |
x dt |
y dt |
|||||||
2. Випадок багатьох незалежних змінних. Якщо z 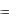 f (x, y) є складна функція багатьох змінних, наприклад z
f (x, y) є складна функція багатьох змінних, наприклад z 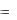 f (x, y) , де x
f (x, y) , де x  (u,v) , y
(u,v) , y  (u, v) , де u і v - незалежні змінні, f , ,
(u, v) , де u і v - незалежні змінні, f , , - диференційовані функції, то частинні похідні z
- диференційовані функції, то частинні похідні z  f (x, y) по u і v
f (x, y) по u і v
виражаються так:
|
dz |
z x |
|
z |
|
y |
, |
|
dz |
|
z x |
|
z |
|
y |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
du |
x u |
|
y u |
|
dv |
|
x v |
|
y v |
||||||||||||
|
Диференціювання неявних функцій |
|||||||||||||||||||||
Якщо рівняння f (x, y) |
0 , де |
f (x, y) |
- диференційована функція змінних x і y |
|||||||||||||||||||
, визначає y як функцію від x , то похідна цієї неявно заданої функції за умови, що
f y' (x, y) 0 , може бути обчислена за формулою
dy |
|
f x' (x, y) |
|||
|
|
|
|
|
. |
dx |
|
f |
' |
(x, y) |
|
|
|
|
y |
|
|

|
Частинні похідні вищих порядків |
|
|
|
|
|
|||||||||||||||
Якщо функція f (x, y) визначена в деякій області D, |
то її частинні похідні |
||||||||||||||||||||
f x (x, y) і f y (x, y) |
також будуть визначені в цій |
області або її |
частині. |
Будемо |
|||||||||||||||||
називати ці похідні частинними похідними першого порядку. |
|
|
|
|
|
||||||||||||||||
Похідні цих функцій будуть частинними похідними другого порядку: |
|
||||||||||||||||||||
|
|
|
2 z |
|
f xx |
(x, y); |
|
2 z |
|
f yy |
(x, y); |
|
|
|
|
|
|||||
|
|
|
x2 |
|
y 2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 z |
f xy |
(x, y); |
|
2 z |
|
f yx (x, y); |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x y |
|
y x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Продовжуючи диференціювати отримані рівності, отримаємо частинні |
|||||||||||||||||||||
похідні більш високих порядків. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Означення. |
Частинні похідні |
виду |
|
|
2 z |
; |
2 z |
; |
|
3 z |
; |
3 z |
і т.д. |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x y |
y x |
x y x |
x y y |
|
||||||
називаються мішаними похідними.
Теорема. Якщо функція f (x, y) і її частинні похідні f x , f y , f xy , f yx визначені і неперервні в точці М(х,у) і її околі, то вірне співвідношення:
2 f |
|
2 f |
. |
|
|
||
x y |
|
y x |
|
Тобто частинні похідні вищих порядків не залежать від порядку диференціювання.
Аналогічно визначаються диференціали вищих порядків.
dz  f x (x, y)dx
f x (x, y)dx  f y (x, y)dy
f y (x, y)dy
d 2 z |
d f |
x |
(x, y)dx f |
y |
(x, y)dy f |
x |
2 (x, y)(dx) |
2 2 f |
xy |
(x, y)dxdy |
|
|
f |
y |
2 (x, y)(dy)2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d |
3 z f |
x |
3 (x, y)(dx)3 |
|
3 f |
2 |
y |
(x, y)(dx)2 dy 3 f |
xy |
2 (x, y)dx(dy)2 |
f |
y |
3 (x, y)(dy)3 |
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
………………….

Похідна за напрямом |
|
|
|||||
Розглянемо функцію u(x, y, z) в точці М(x,y,z) і точці М1(x+ x,y+ |
y, z+ z). |
||||||
Проведемо через точки М і М1 вектор S . Кути нахилу цього вектора до напряму |
|||||||
координатних осей х, у, z позначимо |
відповідно , , |
. Косинуси |
цих кутів |
||||
називаються напрямними косинусами вектора S . |
|
|
|||||
Відстань між точками М і М1 |
на векторі S |
позначимо |
S. |
|
|||
|
|
|
|
|
|
|
|
S |
|
x2 |
y 2 |
z 2 . |
|
|
|
Графічно це виглядає наступним чином:
z
M
S M1
S
y
x
Надалі припустимо, що функція u(x, y, z) неперервна і має неперервні частинні похідні по змінним х, у и z. Тоді має місце наступний вираз:
u |
|
|
u |
x |
u |
y |
|
|
u |
z |
1 x |
2 y |
3 z , |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
y |
|
|
z |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де величини 1, 2, 3 – нескінченно малі при |
S |
0 . |
|
|
||||||||||||
З геометричних міркувань очевидно: |
|
|
|
|
|
|||||||||||
|
x |
|
cos |
; |
|
|
y |
|
cos |
; |
z |
cos |
; |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
S |
|
|
|
S |
|
S |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким чином, наведені вище рівності можуть бути записані наступним чином:

|
u |
|
u |
cos |
|
u |
cos |
|
|
|
u |
cos |
|
cos |
|
|
cos |
|
cos ; |
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|||||||||||||||
|
S |
|
x |
|
y |
|
|
|
|
|
|
z |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
u |
|
lim |
|
u |
|
|
|
|
u |
cos |
u |
cos |
|
u |
cos |
|
|
||||
|
|
|
|
|
|
s |
|
S |
|
|
|
|
y |
|
|
|
|||||||||||
|
|
|
|
|
|
S 0 |
|
|
|
x |
|
|
z |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Відмітимо, що величина s є скалярною. Вона лише визначає напрямок |
|||||||||||||||||||||||||||
вектора S . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
З цього рівняння слідує наступне означення: |
|
|
|
|
|
|
|
||||||||||||||||||||
Означення. |
Границя |
|
lim |
|
|
u |
|
називається |
похідною |
|
функції u(x,y,z) за |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
S |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
S |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
напрямом вектора S в точці з координатами (x,y,z). (див. приклад 1)
Градієнт
Означення. Якщо в деякій області D задана функція u=u(x,y,z) і деякий вектор, проекції якого на координатні осі дорівнюють значенням функції u у
відповідній точці |
u |
; |
u |
; |
u |
, то цей вектор називається градієнтом функції u: |
|||||||
x |
y |
z |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
u |
u |
|
u |
|||
|
|
|
|
|
|
gradu |
|
i |
|
j |
|
k . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
dy |
|
z |
|||
При цьому кажуть, що в області D задано поле градієнтів.
Лінії рівня
Означення. Лінією рівня функції двох змінних z  f (x, y) називається плоска крива, яка утворюється при перетині графіка цієї функції площиною, паралельній координатній площині Oxy z C , де C const .
f (x, y) називається плоска крива, яка утворюється при перетині графіка цієї функції площиною, паралельній координатній площині Oxy z C , де C const .
Лінії рівня, які відповідають різним значенням постійної величини C ,
проецируються на одну площину, наприклад, на координатну площину Oxy ; тоді їх зручно аналізувати і за їх допомогою досліджувати складний характер поверхні,
що описується функцією z  f (x, y) . Таким чином можна сказати, що лінії рівня функції z
f (x, y) . Таким чином можна сказати, що лінії рівня функції z  f (x, y) - це сім‟я кривих, які не перетинаються, на координатній площині Oxy , яка описується рівнянням виду
f (x, y) - це сім‟я кривих, які не перетинаються, на координатній площині Oxy , яка описується рівнянням виду
f (x, y) C .
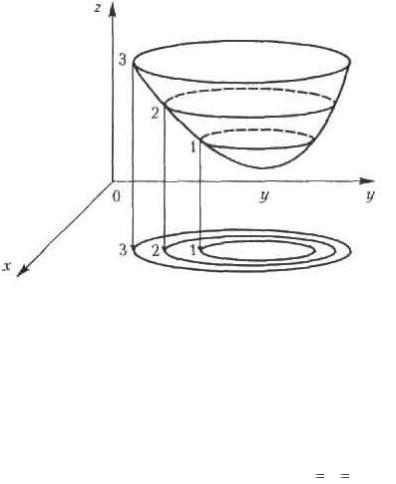
Зазвичай беруть арифметичну прогресію чисел C , з постійною різницею h ;
тоді за взаємним розташуванням ліній рівня можна отримати уявлення про форму поверхні, що описується функцією z  f (x, y) . Там де функція змінюється швидше,
f (x, y) . Там де функція змінюється швидше,
лінії рівня згущуються, а там, де поверхня рівна, лінії рівня розташовуються рідше
(див. рисунок):
Поверхні рівня
Означення. Поверхнею рівня функції u  f (x, y, z) називається поверхня, на якій ця функція зберігає постійне значення
f (x, y, z) називається поверхня, на якій ця функція зберігає постійне значення
u  f (x, y, z) c const .
f (x, y, z) c const .
Лінії та поверхні байдужості Множина еквівалентних з точки зору споживача наборів благ створює
поверхні байдужості. Кількість поверхонь байдужості нескінченна, - кожна людина має свої уподобання, що і відображають системи поверхонь байдужості.
Окремий випадок поверхонь байдужості складають двопродуктові набори товарів.
Для двопродуктових кошиків поверхні байдужості можуть бути зображені набором кривих, які називаються кривими байдужості або індиферентності.
Означення. Лінія байдужості – це лінія рівної корисності, всі точки якої показують множину наборів комбінацій двох благ, що забезпечують один і той же рівень корисності. Кожна крива відображає окремий рівень корисності.
