1.2. Разрешимые и перечислимые множества

Пусть задан некоторый алфавит А, обозначим через Sмножество всех слов в данном алфавите, а через М – некоторое подмножество множестваS.

Определение 1.2.1.Множество М называется разрешимым, если для него существует алгоритм решающий проблему вхождения слова х в М.

Определение 1.2.2.Множества М называется эффективно перечислимым, если существует алгоритм, позволяющий перечислить все элементы этого множества.

Теорема 1.2.1.Если множестваLиMэффективно перечислимы, то эффективно перечислимы множестваLMиLM.

Доказательство.Пусть множестваLиMэффективно перечислимы. Тогда для каждого из них существует алгоритм позволяющий перечислить все элементы данного множества. Алгоритм для эффективного перечисленияLМ иLMполучается путем одновременного применения алгоритмов для эффективного перечисления множеств М иL. Теорема доказана.

Теорема 1.2.2.(Поста) Множество М разрешимо тогда и только тогда, когда оно само и его дополнение эффективно перечислимы.

Доказательство.ПустьМи его дополнение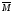эффективно перечислимы, то есть существуют алгоритмы А и В, с помощью которых можно перечислить элементы этих множеств. Но тогда при перечислении множествМив их списке встретится элемент х. Следовательно, существует алгоритм, позволяющий определить, принадлежит элемент х множествуМили не принадлежит.

Пусть множество М разрешимо. Тогда существует алгоритм М, разрешающий проблему вхождения х в М. Пользуясь этим алгоритмом, составим список элементов, входящих в М, и список элементов, входящих в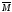. Следовательно, мы получим два алгоритма А и В, позволяющих перечислить множестваМи. Теорема доказана.

Пример.Множество М = {1,4,9,…,n²,…} эффективно перечислимо, так как для получения его элементов надо последовательно брать натуральные числа и возводить их в квадрат. Это множество разрешимо: для проверки того, принадлежит ли число этому множеству (хМ?) достаточно разложить числа на простые множители, что дает возможность установить, является ли оно точным квадратом:

x = 1248 | 2

624 | 2

312 | 2

156 | 2

78 | 2

39 | 3

13 | 13

x= 1248 | 2

624 | 2

312 | 2

156 | 2

78 | 2

39 | 3

13 | 13

Пример.Множество М = {(х,у)|х,у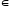N₀}- эффективно перечислимо с помощью так называемого диагонального метода. Выпишем элементы М таким образом:

Перечисление осуществляется последовательным прохождением по диагоналям.

Назовите 10-ый элемент. Ответ: (0,3).

Назовите 20-ый элемент. Ответ: (1,4).

Какой элемент является 27-ым? По возможности, найдите правило нахождения номера любой пары и пары по номеру

Теорема 1.2.3.Существует перечислимое, но неразрешимое множество натуральных чисел.

Доказательство.По теореме Поста достаточно привести пример множества натуральных чиселU, которое само перечислимо, а его дополнение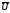не перечислимо.

Пусть М₀, М₁, М₂,… - эффективное перечисление всех перечислимых множеств натуральных чисел, то есть такое перечисление, что по любому номеруnNможно восстановить множествоM_n.

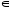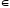Рассмотрим алгоритм А, который последовательно перечисляет элементы множества U. На шаге (m,n) этот алгоритм вычисляет элемент с номеромmмножества М_nи если он совпадает сn, то относит его во множествоU. Итак,nU<=>nM_n

То есть 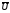отличается от любого перечислимого множества хотя бы одним элементом, так как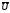состоит из тех элементов, для которыхnM_n. Следовательно,не является перечислимым. По теореме ПостаU- не является разрешимым множеством. Теорема доказана.

Данная теорема включает в себя в неявном виде ранее упоминаемую в логике теорему Геделя о неполноте формальной арифметики. Напомним ее.

В любой непротиворечивой формальной системе, содержащей минимум арифметики, а, следовательно, и в теории натуральных чисел, найдется формально неразрешимое суждение, т.е. такая замкнутая формула А, что ни А ни 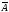не являются выводимыми в системе.