3.Динамический детерминированный оа

Динамический детерминированный ОА имеет код 0=(10γλ). Выходная переменная такого ОА зависит от состояния его входа не только в текущий момент времени. Модель одномерного линейного непрерывного (γ=0, λ=0) объекта представляет собой при этом обыкновенное дифференциальное уравнение вида

(49)

Конечно - разностным аналогом данного дифференциального уравнения является разностное уравнение вида

(50)

Переход от дифференциального уравнения к его конечно-разностному аналогу и наоборот можно осуществить, например, при помощи формул Эйлера. Тогда для преобразования

имеем

Или в общей форме

(51)

где Δt - шаг дискретизации во времени.

Аналогично

(52)

В данном случае используются задания разности. Можно использовать и передние разности. Это не имеет принципиального значения.

Для обратного преобразования, т.е. перехода от разностного уравнения к исходному дифференциальному, на основании (51) и (52) можно записать следующие формулы:

и в общей форме

(53)

Аналогично

(54)

Коэффициенты A_i и B_i уравнения (49) и коэффициенты a_i, b_i уравнения (50) связаны следующим образом:

; (55)

На основании формул (55) можно осуществить переход от разностного уравнения к (исходному) дифференциальному.

Запишем (50) в следующем виде

(56)

Производя в (56) переобозначение переменных, получим уравнение (21)

Справка

Число состояний .

Для нелинейного ОА после линеаризации ММ может быть приведена к виду аналогичному ( ), если вместо самих переменных рассматривать их отклонения. Для описания свойств таких ОА, наряду с дифференциальными уравнениями, широко используются передаточные функции (ПФ). Под ПФ понимают отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях

, (57)

где р - комплексная переменная в преобразовании Лапласа.

ПФ объекта, описываемого обыкновенным дифференциальным уравнением (49), является дробно-рациональной функцией видa

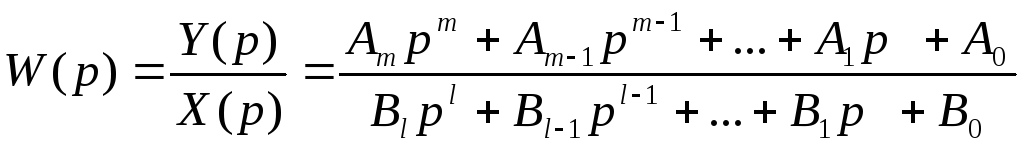(58)

Дифференциальное уравнение (49) и ПФ (58) называют параметрической формой задания ММ, т.к. при идентификации приходится выявлять коэффициенты (параметры) A_i и

B_j.

В качестве непараметрической формы задания ММ используются такие характеристики, как реакция ОА на типовые сигналы:

1. Реакция системы на единичное скачкообразное возбуждение, называемое переходной характеристикой. Скачкообразное возбуждение (функция) имеет вид

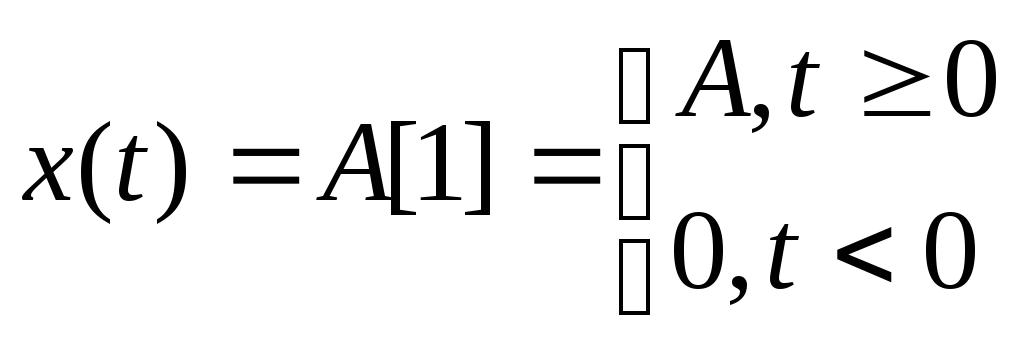(59)

при А = 1 функция называется единичной: x(t)=1(t).

2. Реакция системы на импульсную или -функцию называют импульсной переходнойхарактеристикой или весовой функцией. Импульсная или -функция определяется выражением

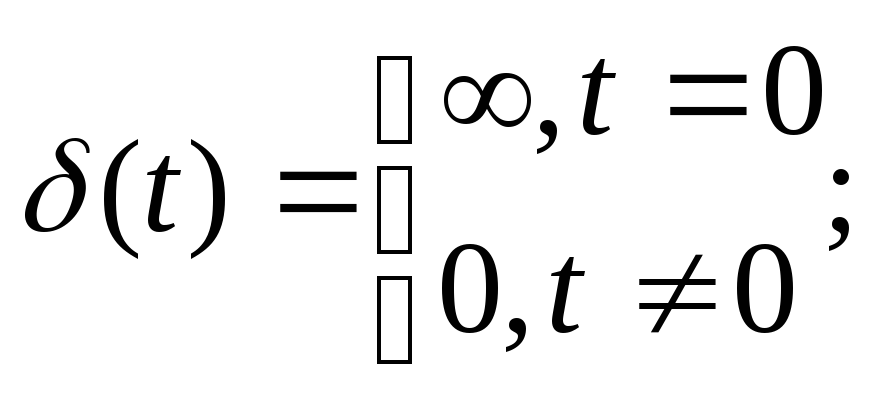
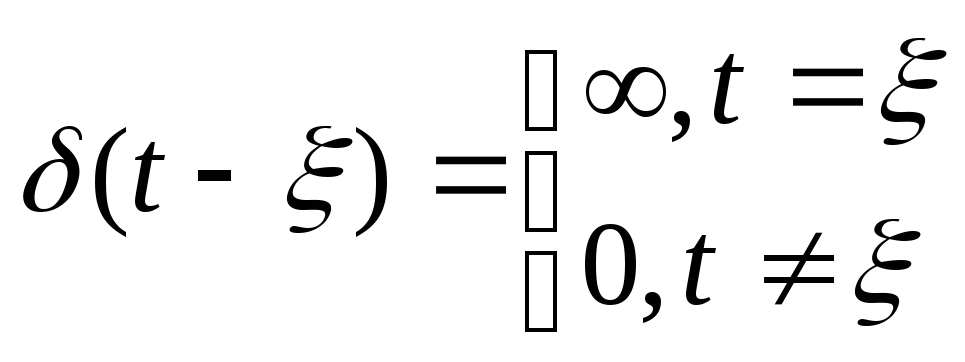(60)

Она является производной от единичной функции 1'(t)

(61)

и обладает свойством

(70)

т.е. ее площадь равна единице. Импульсную функцию можно трактовать как предел прямоугольного импульса, у которого высота стремится к бесконечности, а время его действия - к нулю.

Весовая и переходная функции позволяют оценить временные характеристики систем..

3. Другой распространенный непараметрической ММ линейного (линеаризованного) динамического ОА являются его амплитудная (АЧХ) и фазовая (ФЧХ) частотные характеристики: А() и (). Под АЧХ понимают зависимость относительной амплитуды выходного сигнала ОА от частоты в режиме установившихся гармонических колебаний. ФЧХ характеризует сдвиг по фазе выходного сигнала относительно входного в зависимости от частоты в том же режиме. Входной гармонический сигнал представляется в виде

x = Bcost, (71)

тогда выхддной сигнал

(72)

Описание свойств одномерных линейных ОА в форме весовой функции и частотной характеристики являются эквивалентными, и каждое из них дает исчерпывающую информацию о статических и динамических свойствах объекта.

При синтезе ММ приходится также решать вопрос о том, какие именно входные и выходные переменные будут включены в модель ОА. Для этого прежде всего выявляют все возможные переменные, которые могут «претендовать» на роль входов и выходов ОА, и из них выделяют наиболее существенные. При этом естественно, возникает вопрос, как оценивать «существенность» переменных. Ответ на него определяется целями автоматизации: существенными следует считать те переменные, которые наибольшим образом влияют на достижение поставленных целей. Т.о., задача разработки ММ тесно связана с формированием критериев оптимизации автоматизируемого технологического процесса.