12.3 Нелинейные системы

Существуют динамические явления, которые не могут быть описаны линейными дифференциальными уравнениями с постоянными коэффи­циентами. Нелинейное поведение реальных систем обуславливается раз­личными причинами. Некоторые из них:

• ограничение сигнала в устройствах управления;

• наличие действующих сил, обусловленных сухим трением;

• различные виды реле (с зоной нечувствительности, гистерезисом и т. д.);

• клапаны (зоны нечувствительности, насыщение);

• нелинейные деформации механических пружин;

• аэродинамическое сопротивление;

• двигатели постоянного тока с последовательно включенной обмоткой возбуждения (момент - функция квадрата тока роторной цепи);

• двигатели переменного тока.

В реальных условиях все сигналы ограничены. Примером огра­ничения сигнала может служить обратная связь по току в приводах по­стоянного тока. Ток двигателя должен быть ограничен, иначе двигатель сгорит. Соответственно, система управления двигателем не может быть линейной, особенно при больших ускорениях и моментах нагрузки.

Датчики систем управления также могут иметь нелинейные ха­рактеристики. Такая зависимость может быть линейна при небольших значениях измеряемых сигналов, и существенно нелинейной - для боль­ших. Обычно для нелинейных систем аналитическое решение не может быть получено. Для их решения используются численные методы, что вполне приемлемо в большинстве случаев.

Нелинейные системы можно описать в следующем виде:

(12.1)

где определены n переменных состояния и r входов, или в векторной форме

dx/dt = f(x,u)

В состоянии равновесия производные dx_i/dt равны нулю. Пусть точке равновесия х* соответствует постоянный управляющий сигнал u*, тогда условие равновесия

f(x*,u*)=0

Это уравнение эквивалентно n скалярным уравнениям, и может иметь несколько решений, каждое из которых соответствует некоторой точке равновесия.

12.4 Численное моделирование динамических систем в задачах управления

Для численного решения нелинейных дифференциальных урав­нений применяются различные методы, в основе которых - аппроксима­ция производных по времени разностными уравнениями.

x(t + h)~ x(t) + h f(x(t),u(t)).

Если известны начальные условия х(0), то можно рассчитать значения x(h), x(2h), x(3h), ... , x(nh), которые являются приближениями точного решения в соответствующие моменты времени.

Для решения систем дифференциальных уравнений в процессорных системах управ­ления должны быть определены начальные условия и величина шага интегрирования. Чем меньше шаг интегрирования, тем меньше (фор­мально) погрешность аппроксимации при численном интегрировании. Однако слишком маленький шаг ведет к неоправданно большому време­ни вычислений (которое также зависит от сложности вычислений, типа уравнений, числа переменных и производительности процессора). По­скольку слишком большое значение шага вызывает проблемы сходимости решений, важно определить компромиссное значение. Эффект непра­вильно выбранного шага может оказаться очень существенным, особенно если в моделируемой системе взаимодействуют быстрые и медленные динамические процессы.

Существует много методов численного интегрирования, каждый из которых имеет свои достоинства и недостатки. Наибольшее распро­странение получили методы Рунге-Кутта.

Метод Рунге-Кутта 4-го порядка :

x_i+1 = x_i + h(k₁ + 2k₂ + 2k₃ + k₄)/6,

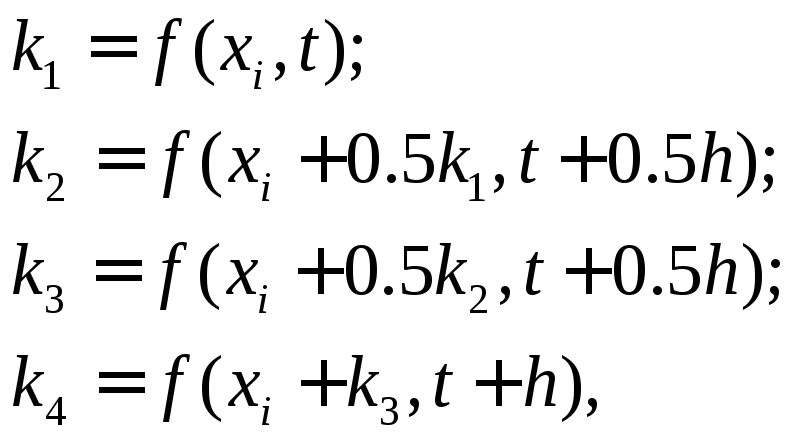
Большинство методов интегри­рования допускают варьируемую величину шага, которая выбирается автоматически, чтобы удовлетворить заданной величине допустимой погрешности. Однако в этом случае невозможно обеспечить получение решения за одинаковые интервалы времени, что важно для систем управления, работающих в реальном времени.