3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.

3.1. Понятие случайной погрешности.

При проведении повторных измерений постоянной физической величины в одинаковых условиях получают результаты измерений, некоторые из которых иногда совпадают друг с другом, но зачастую большинство из них хотя бы незначительно отличаются друг от друга. Причем, расхождения в результатах измерений оказываются хаотическими и не носят систематический характер, что позволяет предположить наличие в результатах измерений случайных погрешностей. Основой таких предположений является следующее:

а) погрешность измерения возникает в результате одновременного воздействия на процесс измерения (объект измерения, средства измерений, оператора, выполняющего измерения, и т.д.) нескольких (многих) источников возмущений. Каждый из источников сам по себе может оказывать на результат измерения незначительное, незаметное влияние; но суммарное воздействие всех (или нескольких) источников может оказаться ощутимым и привести к заметному отклонению его от истинного значения измеряемой физической величины;

б) в любой момент времени указанные источники проявляют себя по разному, действуют независимо друг от друга, без закономерной связи между собой. Такой характер их воздействий приводит к тому, что заметные расхождения в результатах отдельных измерений оказываются различными по размеру и знаку, изменяются хаотически без закономерной связи с предыдущими и последующими, вследствие чего не поддаются непосредственному учету.

Сказанное выше и дает основание говорить о наличии случайных погрешностей в результатах измерений.

Теория вероятностей дает математические методы изучения свойств случайных событий в больших совокупностях. Развитие метрологии и измерительной техники показало, что математический аппарат теории вероятностей и математической статистики полностью соответствует задаче изучения случайных погрешностей измерений; во многих случаях получаемые с его помощью результаты хорошо согласуются с опытными данными измерений. Поэтому он является теоретической основой изучения и анализа случайных погрешностей.

Теория вероятностей называет случайным такое событие, которое при осуществлении определенного комплекса условий может произойти или не произойти. Применяя это определение к области измерений можно сказать, что при проведении повторных наблюдений некоторой физической величины в одинаковых условиях каждая из возможных незначительных причин случайных изменений результатов может или появиться или не появиться. Как следствие, погрешности оказываются непредсказуемыми как по размеру, так и по знаку. Они определяются сложной совокупностью причин, трудно поддающихся анализу.

Исходя из сказанного выше, можно дать следующее определение.

Случайные погрешности, это погрешности: а) изменяющиеся от измерения к измерению; б) не поддающиеся непосредственному учету вследствие их хаотического изменения; в) обусловлены они одновременным воздействием на результат измерения ряда различных, независимых друг от друга факторов.

Присутствие случайных погрешностей, в отличие от систематических, легко обнаруживается при повторных измерениях в виде некоторого разброса результатов измерений.

Таким образом, результат измерений может содержать два вида погрешностей - систематические и случайные (в том числе — грубые погрешности или промахи). Оба вида погрешностей могут проявляться одновременно в результате измерения и погрешность измерения можно представить в виде суммы (а точнее, объединения) двух составляющих:

,

где _S — систематическая, — случайная погрешность.

Случайные погрешности наиболее полно могут быть описаны с помощью закона распределения, в частности — интегральной или дифференциальной функции распределения вероятностей. Случайные погрешности относятся к непрерывным случайным величинам, т.е. они могут принимать нечетное множество значений. Когда говорят о появлении тех или иных случайных погрешностей, имеют в виду вероятность того, что погрешность либо меньше некоторого значения ₁

P(₁)=F(₁),

либо лежит в интервале значений ₁ ... ₂

P(₁₂)=F(₂)–F(₁)/

Функция распределения F() является универсальным способом описания поведения случайных погрешностей. Однако для ее определения требуется проведение кропотливых и обширных экспериментальных и вычислительных работ. К такому способу описания случайных погрешностей в метрологии прибегают только при исследовании принципиально новых СИ.

В технических измерениях задача обработки результатов измерений формулируется следующим образом: а) необходимо определить путем статистической обработки полученного экспериментально ряда результатов наблюдений, который редко бывает большим, оценки параметров функции распределения ряда; б) вид функции распределения ряда, как правило, считается известным из некоторых практических соображений (обычно - нормальное распределение); в) при обработке достаточно получить оценку мат. ожидания (оценку истинного значения ФВ) и оценку разброса (дисперсии), характеризующую плотность группировки результатов наблюдений вокруг мат. ожидания (числовую характеристику случайной погрешности).

3.2. Нормальное распределение случайных погрешностей. Параметры распределения.

Большинство встречающихся на практике случайных величин распределено по нормальному закону (закону Гаусса). К числу таких случайных величин относится большая часть случайных погрешностей измерений. Плотность нормального распределения для случайной величины Х описывается уравнением:

,

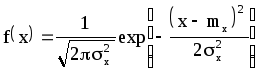где: m_x=М[Х] — математическое ожидание случайной величины; — дисперсия.

Нормальное распределение случайной величины Х полностью задается двумя характеристиками — m_x и ², которые называют параметрами нормального распределения.

Математическое ожидание случайной величины — это наиболее вероятное ее значение, т.е. такое значение вокруг которого группируются результаты отдельных наблюдений. Если наблюдается нормальное распределение случайных погрешностей измерений, то их математическое ожидание равно нулю. Если же рассматривать нормальное распределение результатов наблюдений, то их математическое ожидание соответствует истинному значению измеряемой физической величины. Последнее справедливо в случае, если систематические погрешности полностью исключены.

Мерой рассеяния значений случайной погрешности служит дисперсия , которая для случайной непрерывной величины (случайной погрешности ), как известно, определяется выражением:

,

где -функция плотности вероятности случайной погрешности.

Дисперсия имеет размерность квадрата измеряемой физической величины, поэтому с точки зрения размерности она не совсем удобна в качестве характеристики рассеивания (а значит и случайной погрешности). На практике в качестве последней чаще используют положительное значение корня квадратного из дисперсии — среднее квадратическое отклонение (СКО) результатов наблюдений:

.

СКО соответствует характерной точке нормального распределения: вероятность того, что случайная погрешность измерения не выйдет за пределы  составляет

,

т.е. вероятность попадания случайной погрешности в интервал с границами  в два раза больше, чем вне этого интервала.

Нормальное распределение следует рассматривать как теоретическую основу для изучения случайных погрешностей и их влияния на результат измерения. Широкое применение нормального распределения в практике измерений объясняется центральной предельной теоремой теории вероятностей. Она утверждает, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под воздействием большого числа независимых факторов, каждый из которых оказывает лишь незначительное влияние по сравнению с суммарным влиянием всех остальных (формулировка теоремы дана в применении к случайным погрешностям).

Иногда в практике измерений используется равномерное распределение, описываемое:

,

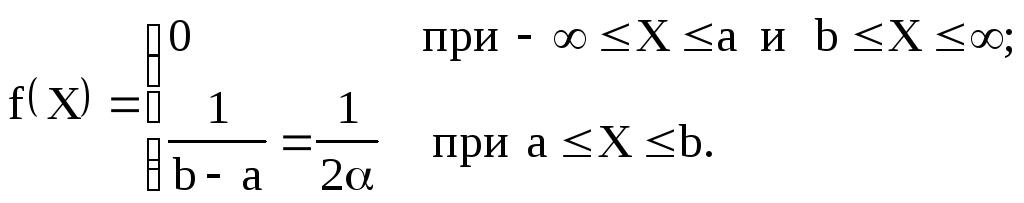Для него .

3.3. Точечные оценки истинного значения фв и ско, получаемые на основании ограниченного ряда наблюдений.

Повторив несколько раз наблюдения, мы получим ряд числовых значений измеряемой величины. Эти значения большей частью отличаются одно от другого, но если измерения проводились в одинаковых условиях и с одинаковой тщательностью, то все заслуживают одинакового доверия. Возникает вопрос, как на основании полученной в эксперименте группы результатов наблюдений оценить истинное значение измеряемой ФВ, т.е. как получить результат измерения, и как оценить его точность, т.е. меру приближения к истинному значению. Эта задача является частным случаем задачи нахождения статистических оценок параметров функции распределения случайной величины на основании выборки — ряда значений, полученных в n независимых опытах. Поскольку результаты наблюдений обычно распределены нормально, то оцениваемыми параметрами, как правило, являются МО и СКО, которые входят в выражения для дифференциальных функций нормального распределения случайных погрешностей и результатов наблюдений.

При обработке результатов наблюдений желательно получать оценку «параметра», которая выражается одним числом. Такую оценку называют точечной. Любая точечная оценка, полученная на основании опытных данных, является их функцией и представляет собой случайную величину, распределение которой зависит от распределения исходной случайной величины (результатов наблюдений) и числа опытов n. К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания параметров:

-оценка должна быть состоятельной, т.е. при увеличении n она должна приближаться к значению оцениваемого параметра: (где А – оцениваемый параметр, - оценка параметра);

-оценка должна быть несмещенной, т.е. ее МО должно быть равно оцениваемому параметру: М[]=А;

-оценка должна быть эффективной, т.е. ее дисперсия должна быть меньше дисперсии любой другой оценки данного параметра (т.е. минимальна): D[]=min.

Существуют несколько методов определения оценок. Наиболее распространен метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Получаемые с помощью этого метода оценки называют оценками максимального правдоподобия. Основное достоинство оценок максимального правдоподобия заключается в том, что они являются асимптотически (при n) несмещенными, асимптотически эффективными, асимптотически нормально распределенными.

Для наиболее часто встречающегося на практике нормального распределения результатов наблюдений оценкой максимального правдоподобия для истинного значения ФВ (т.е. для мат.ожидания) является среднее арифметическое результатов отдельных наблюдений, а оценкой дисперсии — среднее значение квадратов отклонений результатов наблюдений от среднего арифметического:

;

.

Оценка СКО результатов наблюдений определяется следующим образом:

и характеризует в среднем точность любого отдельного результата наблюдения в серии результатов.

*Среднее значение бесконечно большого числа наблюдений (n) стремится к истинному значению измеряемой ФВ. Практически среднее значение, как правило, определяется на основании конечного числа наблюдений. Поэтому оно отличается от истинного значения ФВ на величину , которая является случайной погрешностью среднего значения:

.

При увеличении числа наблюдений значение погрешности среднего арифметического уменьшается и при n погрешность .

В мат. статистике установлено, что:

а) случайные погрешности средних значений подчиняются нормальному закону распределения вероятностей, если случайные погрешности результатов отдельных наблюдений распределены нормально. Т.е. если результаты наблюдений распределены нормально, то и средние значения результатов наблюдений распределены нормально;

б) дисперсия средних значений результатов наблюдений меньше дисперсии результатов отдельных наблюдений.

При этом теория вероятностей даёт следующее соотношение между дисперсией результатов наблюдений и дисперсией средних значений результатов наблюдений :

n - число наблюдений.

Для средних квадратических отклонений справедливо следующее соотношение:

,

где σ – СКО результатов наблюдений; σ() – СКО среднего значения (СКО результата измерения).

Для статистических оценок СКО получаем:

и .

Вывод: СКО результата измерения σ() при увеличении числа наблюдений в «n» раз теоретически уменьшается в раз.

Таким образом, СКО среднего из «n» наблюдений в раз меньше СКО результатов наблюдений. Иными словами, если за результат измерения принять результат единичного наблюдения, то случайную погрешность такой оценки будет характеризовать СКО «σ», а если усреднить результаты наблюдений и принять среднее по «n» наблюдениям за оценку измеряемой величины, то случайную погрешность такой оценки будет характеризовать СКО «σ()», т.е. в раз меньшее.

Вывод: хоть исключить случайные погрешности совсем нельзя, можно уменьшить их влияние на результат измерения. Для этого необходимо выполнить серию наблюдений; причем, чем меньшее значение погрешности допустимо оставить неисключенной, тем больше должна быть эта серия. Однако необходимо четко понимать, что если случайная погрешность, полученная для серии наблюдений, окажется значительно меньше погрешности, определяемой классом точности прибора (т.е. инструментальной), нет смысла еще уменьшать значение случайной составляющей погрешности: все равно результат измерений не станет от этого точнее. Если же случайная погрешность больше инструментальной, следует произвести ряд (серию) наблюдений, чтобы уменьшить случайную погрешность и сделать ее меньше или хотя бы одного порядка с погрешностью прибора.

Итог измерений с помощью точечных оценок записывается в виде:

Что уже позволяет сделать выводы относительно точности измерений.