
- •Числовые ряды Лекция № 44. Тема 1 : Числовой ряд. Необходимый признак сходимости
- •1.2. Необходимый признак сходимости. Гармонический ряд
- •Лекция № 45
- •2.2. Признак Даламбера
- •2.3. Радикальный признак Коши
- •2.4. Интегральный признак Коши
- •Тема 3 : Знакопеременные ряды
- •3.1. Знакочередующиеся ряды. Теорема Лейбница
- •3.2. Абсолютная и условная сходимость
- •Список литературы
- •С о д е р ж а н и е
Числовые ряды Лекция № 44. Тема 1 : Числовой ряд. Необходимый признак сходимости
1.1. Числовой ряд и его сумма
Определение 1.
Пусть дана числовая последовательность
![]() .
Образуем выражение
.
Образуем выражение
 (1)
(1)
которое
называется
числовым
рядом.
Числа
![]() называютсячленами
ряда,
а выражение
называютсячленами
ряда,
а выражение
![]()
общим
членом
ряда.
общим
членом
ряда.
Пример
1.
Найти общий член ряда
![]() .
.
При
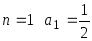 ,
,
при
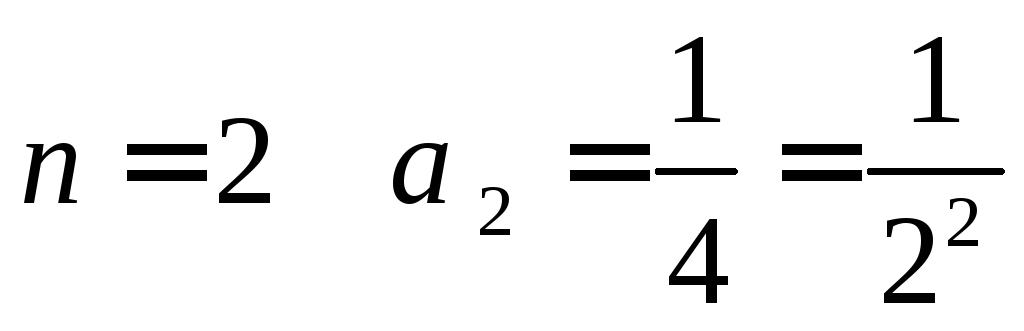 ,
,
при
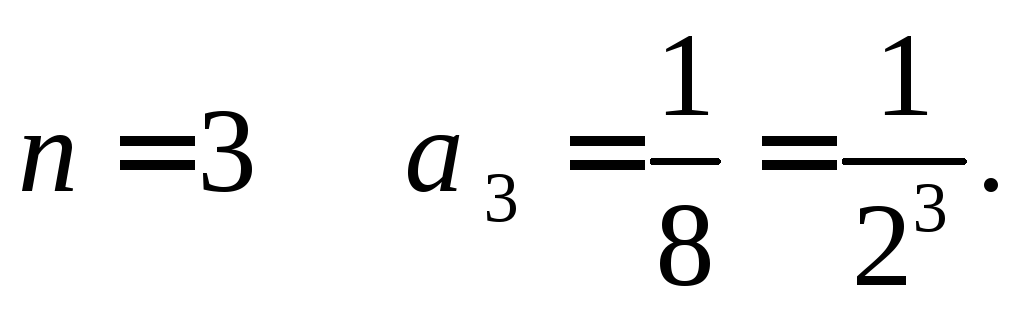
Нетрудно
заметить, что общий член ряда
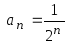 .
.
Поэтому искомый ряд можно записать следующим образом
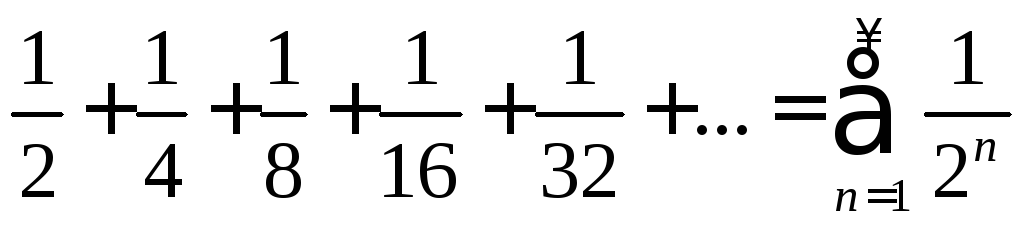 .
.
Построим из членов ряда (1) последовательность таким образом:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
Каждый член этой последовательности представляет собой сумму соот-ветствующего числа первых членов числового ряда.
Определение 2. Сумма первых п членов ряда (1) называется n-ой частичной суммой числового ряда.
Определение
3.
Числовой ряд
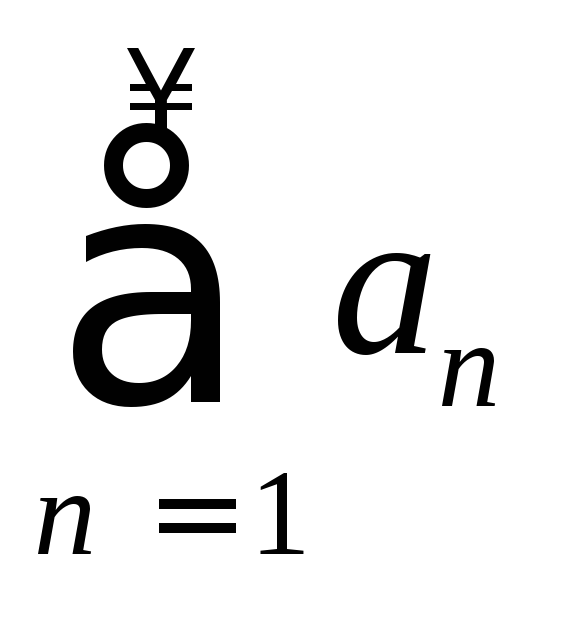 называетсясходящимся,
если
называетсясходящимся,
если
![]() ,
где число
,
где число![]() называетсясуммой
ряда,
и пишут
называетсясуммой
ряда,
и пишут
![]() .
Если
.
Если
предел частичных сумм бесконечен или не существует, то ряд называется расходящимся.
Пример
2.
Проверить
на сходимость ряд
![]() .
.
Для
того, чтобы вычислить n-ю
частичную сумму
![]() представим общий член
представим общий член![]() ряда
ряда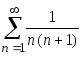 в виде суммы простейших дробей
в виде суммы простейших дробей
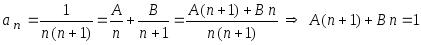
Сравнивая коэффициенты при одинаковых степенях n, получим систему линейных алгебраических уравнений относительно неизвестных коэффици-ентов А и В

Отсюда
находим, что
![]() ,
а
,
а![]() .
.
Следовательно,
общий член ряда имеет вид
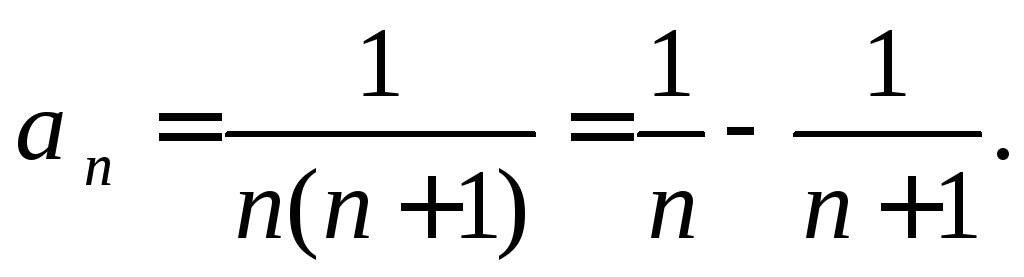
Тогда
частичную сумму
![]() можно представить в виде
можно представить в виде
![]() .
.
После раскрытия скобок и приведения подобных членов, она примет вид
![]() .
.
Вычислим сумму ряда
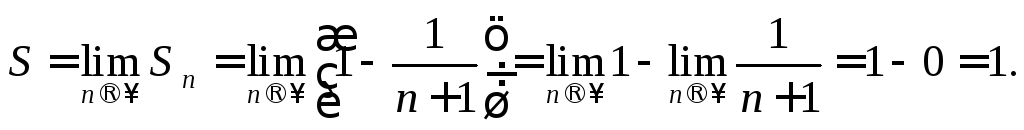
Так как предел равен конечному числу, то данный ряд сходится.
Пример
2.
Проверить
на сходимость ряд
![]()
бесконечную геометрическую прогрессию.
Как
известно, сумма первых п
членов геометрической прогрессии при
q
![]() 1
равна
1
равна
 .
.
Тогда имеем следующие случаи:
1.
Если
![]() ,
то
,
то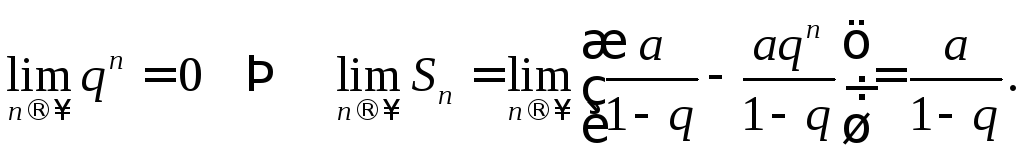
2.
Если
![]() ,
то
,
то![]() ,
т.е. ряд расходится.
,
т.е. ряд расходится.
3.
Если
![]() ,
то ряд имеет вид
,
то ряд имеет вид![]() и тогда
и тогда![]() ,
т.е. ряд расходится.
,
т.е. ряд расходится.
4.
Если
![]() ,
то ряд имеет вид
,
то ряд имеет вид![]() и тогда
и тогда![]() ,
если частичная сумма имеет четное число
членов и
,
если частичная сумма имеет четное число
членов и![]() ,
если нечётное число, т.е.
,
если нечётное число, т.е.![]() не существует, следовательно, ряд
расходится.
не существует, следовательно, ряд
расходится.
Определение
4.
Разность между суммой ряда S
и частичной суммой
![]() называетсяостатком
ряда
и обозначается
называетсяостатком
ряда
и обозначается
![]() ,
т.е.
,
т.е.![]() .
.
Так
как для сходящихся рядов
![]() ,
то
,
то![]() ,
,
т.е.
![]() будет б.м.в. при
будет б.м.в. при![]() .
Таким образом, значение
.
Таким образом, значение![]() является приближенным значением суммы
ряда.
является приближенным значением суммы
ряда.
Из определения суммы ряда следуют свойства сходящихся рядов:
1.
Если ряды
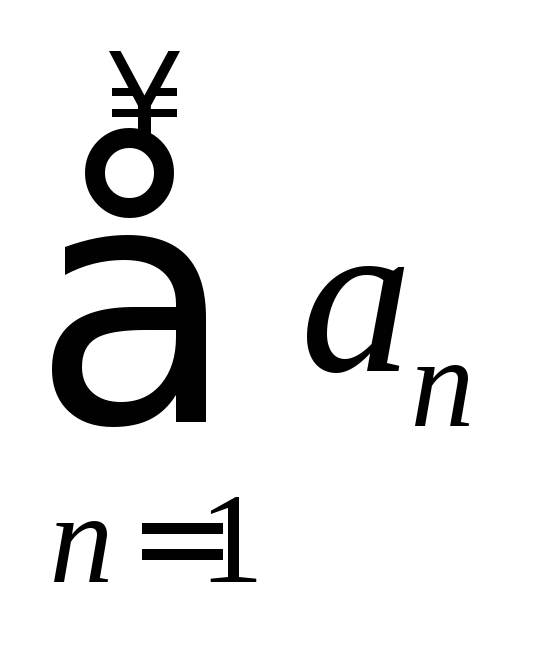 и
и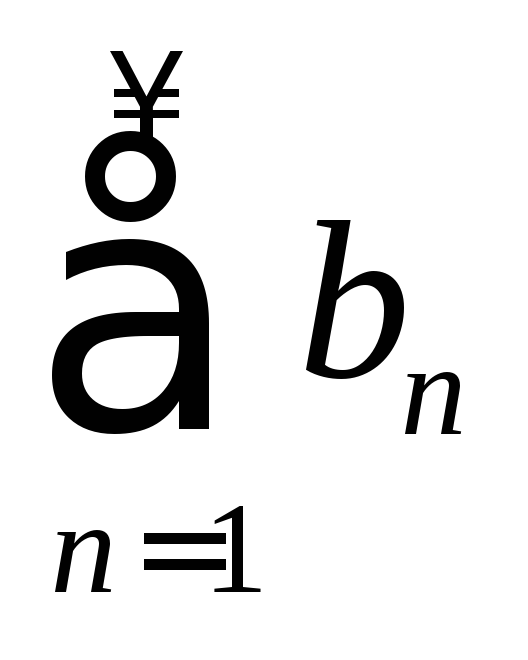 сходятся, т.е. имеют соответственно
суммыS
и Q,
то сходится ряд
сходятся, т.е. имеют соответственно
суммыS
и Q,
то сходится ряд
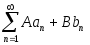 ,
где
,
где![]() ,
а его сумма равнаA
S
+
B
Q.
,
а его сумма равнаA
S
+
B
Q.
2.
Если
сходится
ряд
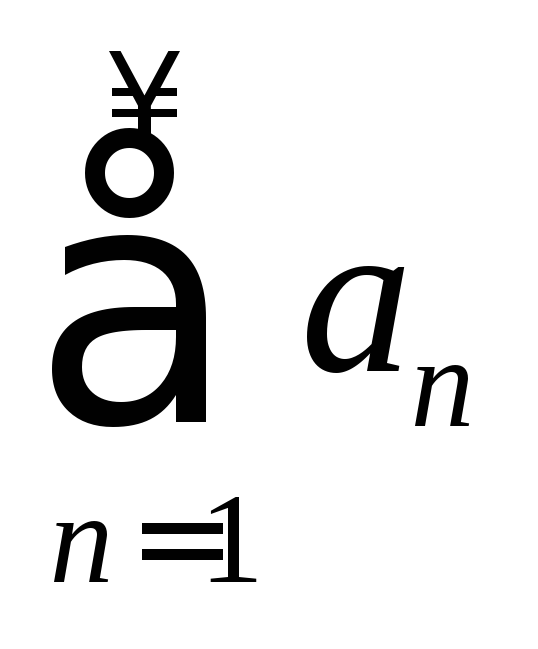 ,
то сходится и ряд, полученный из данного
,
то сходится и ряд, полученный из данного
ряда отбрасыванием или добавлением конечного числа членов. Верно и обратное.
1.2. Необходимый признак сходимости. Гармонический ряд
Теорема.
Если ряд
![]() сходится,
то общий член ряда стремится
к
нулю
при
сходится,
то общий член ряда стремится
к
нулю
при
![]() ,
т.е.
,
т.е.![]() .
.
Действительно, имеем
![]() ,
,
тогда
![]() ,
что
и требовалось доказать.
,
что
и требовалось доказать.
Следствие.
Если
же
![]() ,
то ряд расходится.
Обратное, вообще говоря, неверно, что
будет показано ниже.
,
то ряд расходится.
Обратное, вообще говоря, неверно, что
будет показано ниже.
Определение
5.
Ряд вида
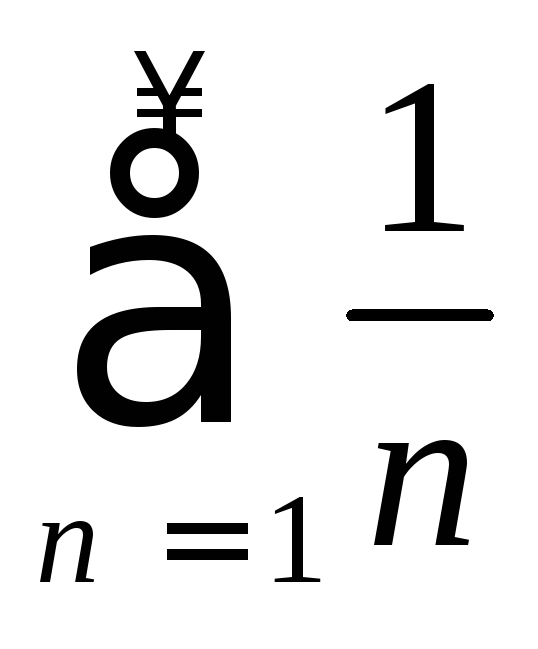 называется
гармоническим.
называется
гармоническим.
Для
этого ряда выполняется необходимый
признак, так как
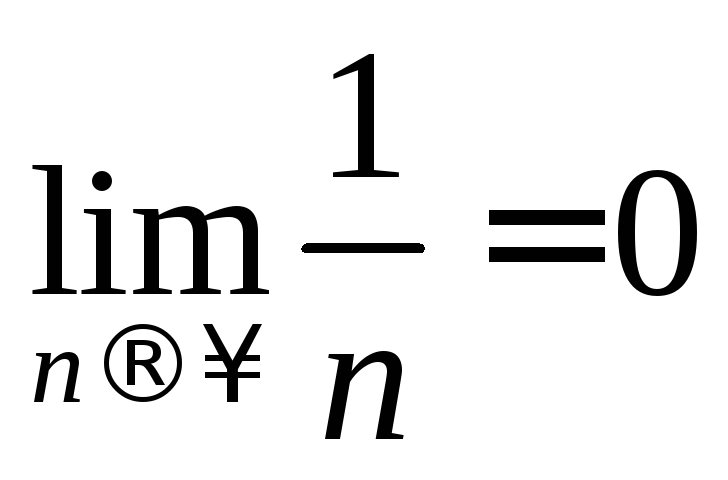 .
.
В то же время он является расходящимся. Покажем это
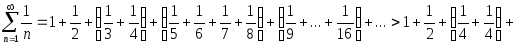
![]()
Таким образом, гармонический ряд расходится.
Тема 2 : Достаточные признаки сходимости рядов
с положительными членами
2.1. Признаки сравнения
Пусть даны два ряда с положительными членами:
![]() (1)
(1)
![]() (2)
(2)
Признак
сравнения.
Если для всех членов рядов (1) и (2), начиная
с некоторого номера, выполняется
неравенство
![]() и ряд (2) сходится, то сходится и ряд (1).
Аналогично, если
и ряд (2) сходится, то сходится и ряд (1).
Аналогично, если![]() и ряд (2) расходится, то расходится и
ряд (1).
и ряд (2) расходится, то расходится и
ряд (1).
Пусть
![]() и
и![]() соответственно частичные суммы рядов
(1-2), аQ
сумма ряда (2). Тогда для достаточно
больших п
имеем
соответственно частичные суммы рядов
(1-2), аQ
сумма ряда (2). Тогда для достаточно
больших п
имеем
![]() .
.
Так
как
![]() и ограничена, то
и ограничена, то![]() ,
т.е. ряд (1) сходится.
,
т.е. ряд (1) сходится.
Аналогично доказывается и вторая часть признака.
Пример 3. Исследовать на сходимость ряд
![]() .
.
Сравним
с членами ряда
![]() .
.
Начиная
с
![]() ,
имеем
,
имеем .
.
Так
как
ряд
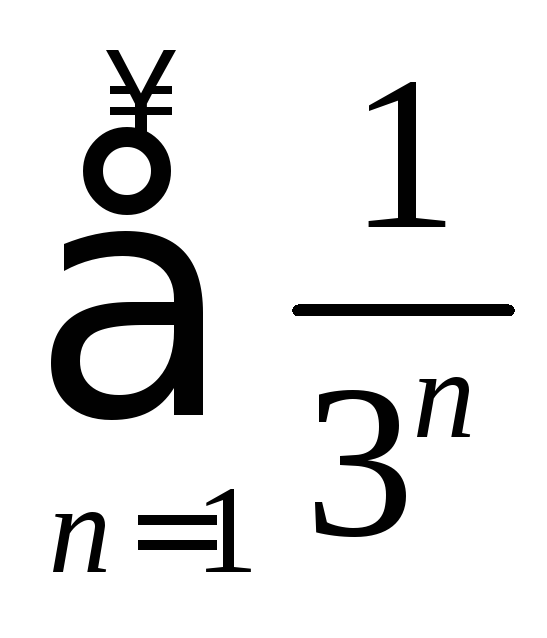 сходится
сходится![]() ,
то
данный
ряд
также
сходится.
,
то
данный
ряд
также
сходится.
На практике часто более удобно пользоваться так называемым предельным признаком сравнения, который вытекает из предыдущего.
Предельный
признак сравнения.
Если
для двух рядов (1-2) с положи-тельными
членами выполняется условие
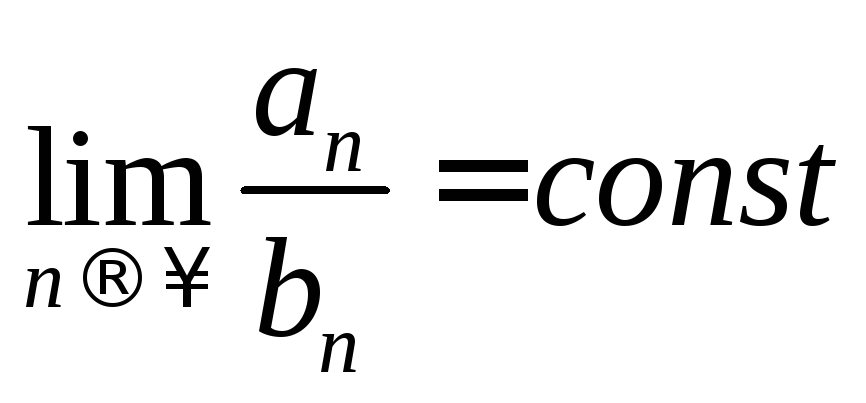
![]() ,
то
,
то
из сходимости ряда (1) следует сходимость ряда (2), а из расходимости ряда (1) следует расходимость ряда (2), т.е. ряды ведут себя одинаково.
Пример
4.
Исследовать на сходимость ряд
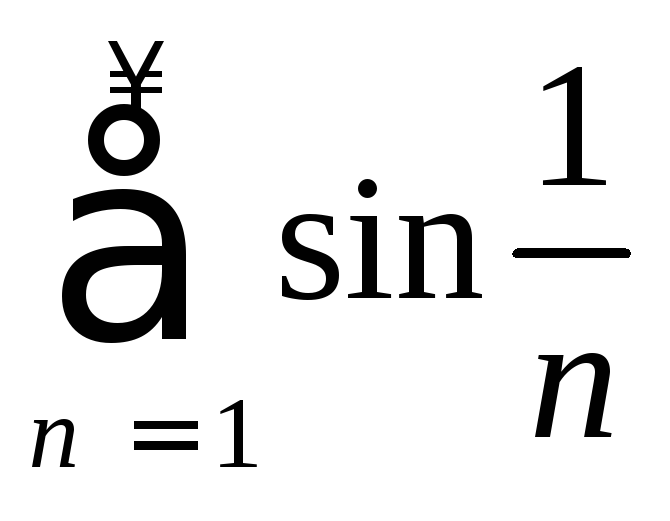 .
.
В
качестве ряда для сравнения возьмем
гармонический ряд
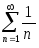 ,
,
который является расходящимся.
Тогда
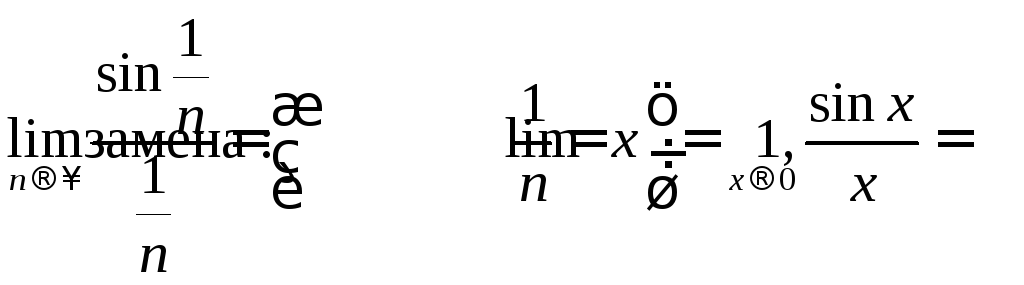
а, следовательно, наш ряд расходится.
Замечание.
Часто для сравнения удобно использовать
так называемый обобщённый
гармонический
ряд
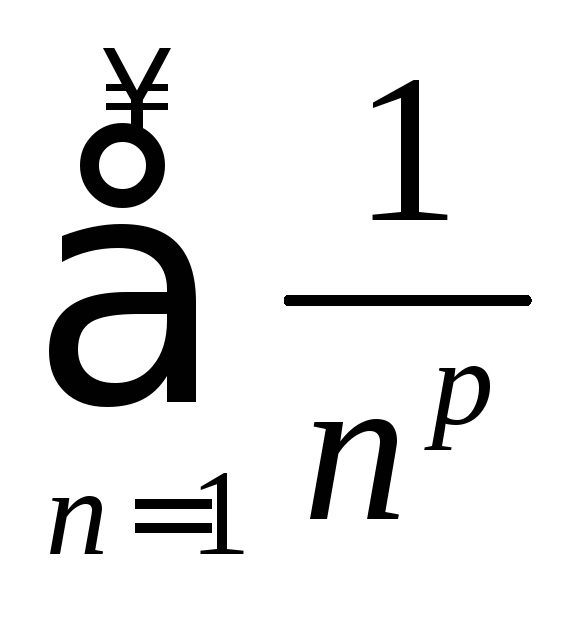 ,
который, как будет показано ниже,
сходится при
,
который, как будет показано ниже,
сходится при![]() и расходится при
и расходится при![]() .
.
