Релятивістський закон додавання швидкостей

Якщо матеріальна точка рухається паралельно до осі х , то швидкість відносно системиК збігається з _х а швидкість ´з _х´.Тоді

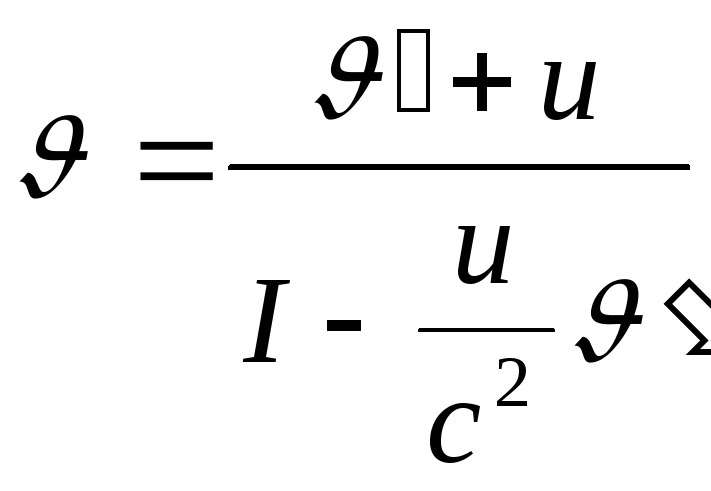, (1.87)

де - швидкість матеріальної точки в системіК,

´- швидкість матеріальної точки в системі К,

и – швидкість системи Квідносно К.

Якщо швидкості ´,іи малі порівняно з швидкістю с ,то ,. (1.88)

Якщо ´=с, то =с. При додаванні довільних швидкостей результат не може перевищити швидкість світла с у вакуумі. Із формули (1.88) випливає, що швидкість світла у вакуумі є граничною швидкістю і не може бути пере-вищена ні за яких умов, навіть у разі додавання швидкостей.

§3. Поняття про релятивістську динаміку

З принципу відносності (всі інерціальні системи рівноправні) випливає, що математичний запис будь-якого закону фізики повинен бути однаковим в усіх інерціальних системах відліку. Цю умову називають умовою інваріантності фізичних законів відносно перетворень Лоренца. Розглянемо основний закон класичної динаміки:

або , (1.89)

де m=соnst.

Рівняння (1.89) інваріантне по відношенню до перетворень Галілея. Але рівняння (1.89) неінваріантне по відношенню до перетворень Лоренца. Ейнштейн показав, що маса є функція швидкості руху:

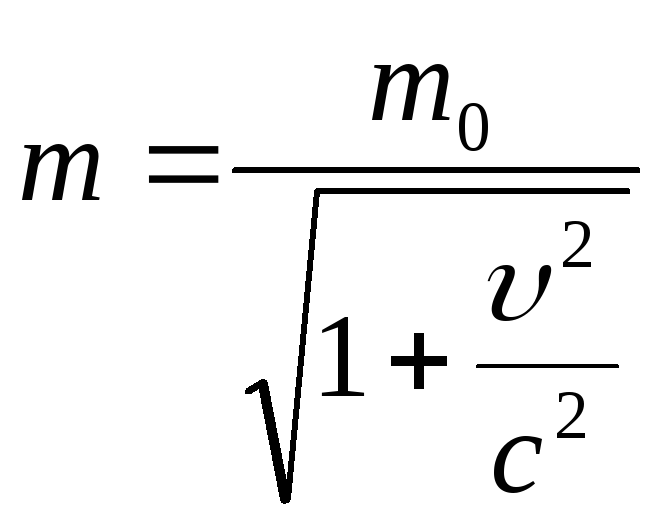, (1.90)

де m₀ –маса спокою матеріальної точки чи тіла, m - релятивістська маса .

Якщо ,m ( Рис.1.16 ).

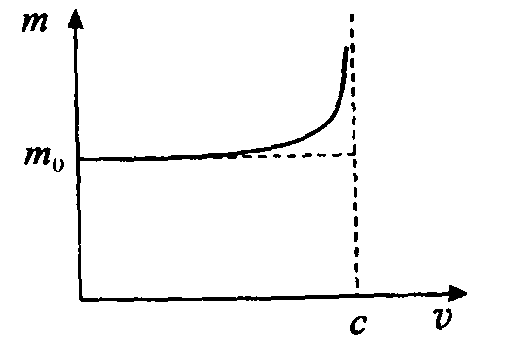
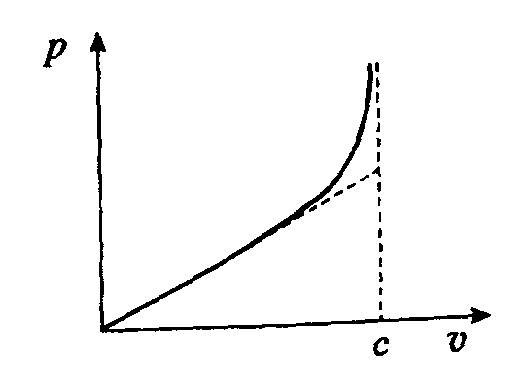
Рис.1.16 Рис.1.17

Релятивістський імпульс , на відміну від класичної механіки, є нелінійною функцією її швидкості (рис.1.17):

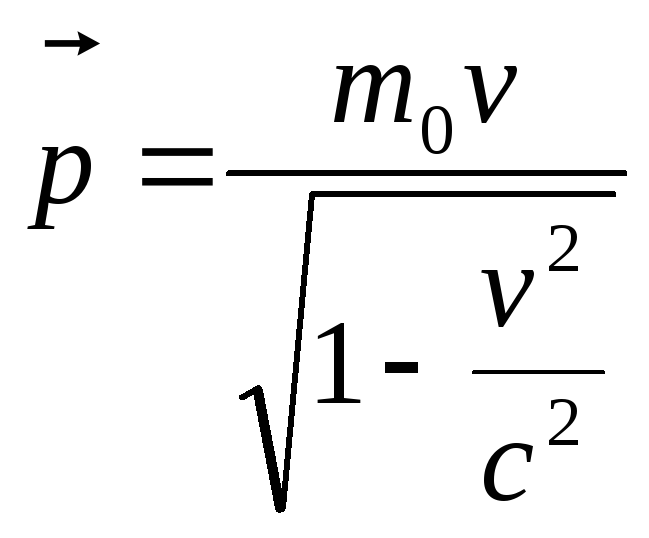, (1.91)

Якщо , Р .

Основний закон релятивістської динаміки : швидкість зміни імпульсу матеріальної точки дорівнює силі , що діє на цю точку має вигляд:

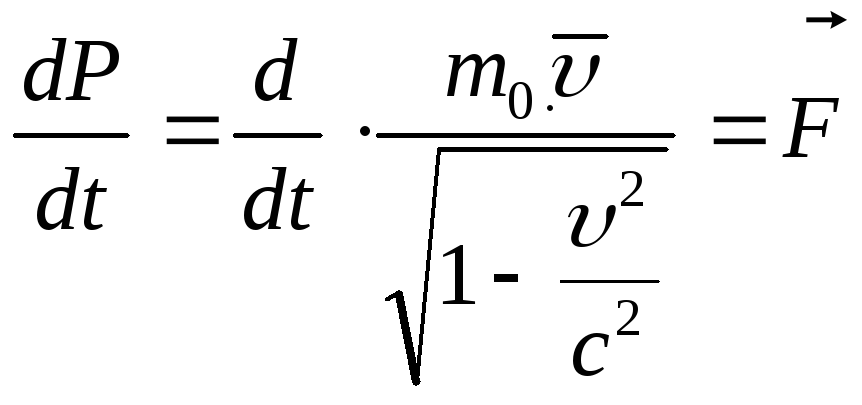. (1.92)

Ейнштейн показав також , що маса і енергія взаємозв’язані співвідношенням

(1.93)

Закон взаємозв’язку маси і енергії називають ще законом пропорційності маси і енергії . Він означає, що маса і енергія зростають або зменшуються одночасно. Якщо енергія тіла (частинки) змінюється на величину , то одночасно змінюється і його маса на відповідно до формули

. (1.94)

Отже, не може бути мови про зведення маси до енергії . Можна стверджувати, що енергія і маса – властивості матерії, що рухається.

Релятивістський вираз кінетичної енергії має вигляд:

Т=Е-Е₀ =mc²-m₀c²,

. (1.95)

Релятивістський зв’ язок між кінетичною енергією й імпульсом :

, (1.96)

де Т- релятивістська кінетична енергія, с - швидкість світла, Е₀ - енергія спокою.

Релятивістський зв’ язок між повною енергією й імпульсом:

Е²=mc²=m₀²c⁴+p²c² , (1.97)

де Е₀=m₀c² - енергія спокою тіла.

Теорія відносності спростувала уявлення класичної механіки про взаємну незалежність простору і часу та незалежність їх від матеріальних тіл. Єдиний закон збереження маси й енергії в теорії відносності свідчить про однорідність єдиного просторово-часового світу.

ПРИКЛАДИ РОЗВ'ЯЗАННЯ ЗАДАЧ

Задача 1. Диск радіусом R=5 см обертається навколо нерухомої осі так, що залежність кутової швидкості від часу задається рівнянням = 2Аt + 5Вt ⁴ (А=2рад/с², В=1рад/с⁵) Визначити для точок на ободі диска до кінця першої секунди після початку руху:1) повне прискорення; 2) число обертів, зробле-них диском.

Дано:R=5см=0,05м; =2Аt+5Вt⁴; А=2рад/с²; В=1рад/с⁵; t=1с.

Визначити: 1)а; 2)N.

Розв’язання. Повне прискорення , де тангенціальна складова прискорення(-кутове прискорення), а нормальна складова прискорення .

За умовою задачі отже,

,

,

Звідси повне прискорення

Кут повороту диска ( N- число обертів), але кутова швидкість отже,

.

Тоді число обертів, зроблених диском, ,

Перевіримо одиниці виміру.

[а]=м=м/с² , N - одиниць виміру не має.

Підставивши числові дані, одержимо:

а ==4,22(м/с²),

N==0,4770,5.

Відповідь : 1) а = 4,22 м/с ² , 2 ) N0,5.

Задача 2. На барабан радіусом R=20см, момент інерції якого J=0,1 кгм², намотаний шнур до кінця якого прив'язаний вантаж массою m=0,5кг. До початку обертання барабана (рис.1) висота вантажу над підлогою h ₀=1м. Через який час t вантаж опуститься до підлоги? Знайти кінетичну енергію W_k вантажу в момент удару об підлогу і силу натягу нитки Т. Тертям зневажити.

Дано:R=20cм=0,2м, J=0,1кгм² , m=0,5кг, h₀=1м

Визначити:1)t; 2)Wk; 3)Т.

Розв’язання. При опусканні вантажу його потенціальна енергія переходить у кінетичну енергію поступального руху і кінетичну енергію обертального руху:

(1), де ,

відкіля

,

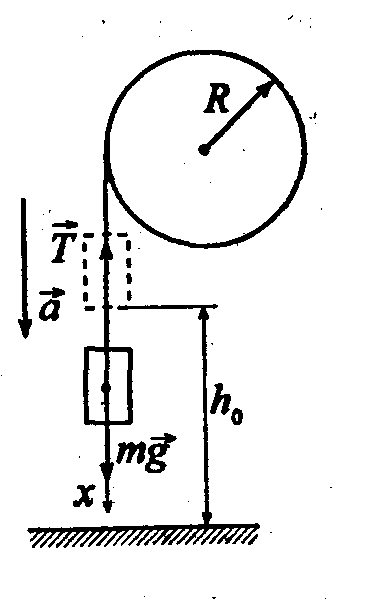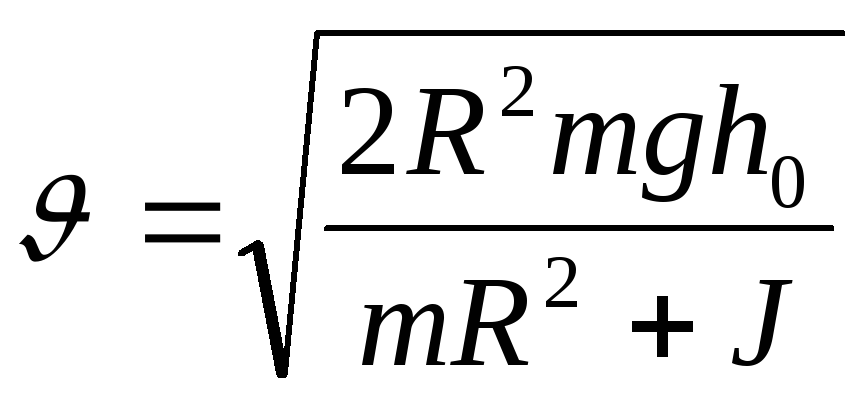; (2)

Рух рівноприскорений , тому Рис.1

(3) Рис.1

(4)

Виразимо t з (4) і підставивши в (2) одержимо: ;

Кінетична енергія , підставивши рівняння (2), одержимо:

.

Відповідно до другого закону Ньютона

mg -T= ma , відкіля T= m(g-а) .

З (3) ,

Тоді.

Перевіримо одиниці виміру і проведемо обчислення t, W_к і Т.

=с,

, .

кгм/с²=Н

Відповідь: t=1,1с; W_k=0,82Дж; Т=4,1Н.

Задача 3. Куля, що летить горизонтально, попадає в кулю, підвішену на невагомому твердому стрижні, і застряє в ньому. Маса кулі в 1000 разів менше маси кулі. Відстань від центра кулі до точки підвісу стрижня =1м. Знайти швидкість кулі, якщо відомо, що стрижень з кулею відхилився від удару кулі на кут (рис.2).

Дано:М=1000 m , =1м, .

Визначити .

Розв’язання.

Силу опору повітря не враховуємо, отже, систему "куля _m- куля _M" можна вважати замкнутою. Запишемо закон збереження імпульсу й енергії для даної системи:

m=(m+M)u (1)

де u- швидкість кулі_m разом з кулею_M після удару. У результаті взаємодії куль, після відхилення стрижня на < , їх кінетична енергія перейшла в потенціальну енергію

(2).

З (1) виразимо u:

u = або u = = . Рис.2 З (2) одержимо: .

Знайдемо h.

ВМ=,h=;,тоді

.

Перевіримо одиниці виміру .

Проведемо обчислення .

Відповідь =550м/с.

Задача 4.Знайти роботу А, яку треба виконати, щоб стиснути пружину на =20 см, якщо відомо, що сила F пропорційна стиску і твердість пружини k=2,94 кН/м.

Дано: = 20 см = 0,2м, k = 2,94кН/м=2,94* 10³ Н/м.

Визначити А.

Розв’язання. Робота, виконана при стиску пружини, визначається формулою

(1),

де- стиск. За умовою сила пропорційна стиску, тобто

F= - k(2).

Підставляючи (2) у (1), одержимо

.

А=58,8Дж.

Перевіримо одиниці виміру А.

.

Проведемо обчислення А.

Відповідь А=58,8 Дж.

Задача 5. Камінь кинутий горизонтально з швидкістю v _x=10м/с. Знайти радіус кривизни R траєкторії каменю через час t=3с після початку руху (рис.3).

Д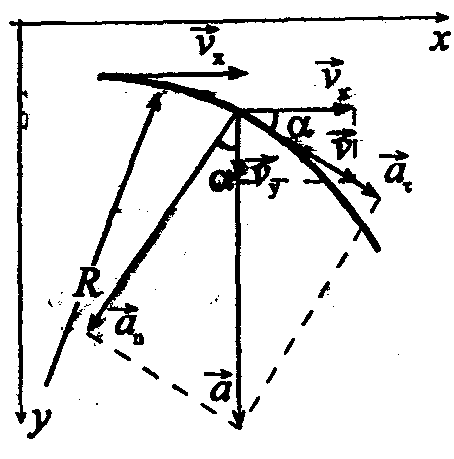ано: _x=10м/с, t=3с.

Визначити R.

Розв’язання. Нормальне прискорення каменю

(1);

З рисунку видно, що

(2).

З рівняння (1) Рис.3

, де .

Крім того ; .

Зробивши відповідні підстановки, одержимо

.

Перевіримо одиниці виміру і проведемо обчислення шуканої величини.

, R=.

Відповідь R=305м.

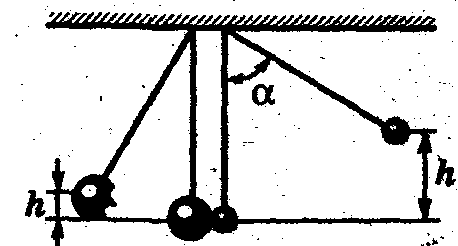
Задача 6. Дві свинцевих кулі масами m₁=2кг і m₂=3кг підвішені на нитках довжиною =70см. Спочатку кулі стикаються між собою, потім меншу ку-

лю відхили на кут=60⁰ і відпустили (рис.4). Вважаючи удар центральним і непружним, визначити :1) висоту h , на яку піднімуться кулі після удару;

2) енергію, затрачену на деформацію куль при ударі.

Дано: m₁=2кг, m₂=3кг, =70см=0,7м, =60⁰.

Визначити: 1) h; 2) .

Розв’язання .Удар непружний, тому після удару кулі рухаються із загальною швидкістю , яку знайдемо із закону збереження імпульсу

(1)

де ₁ і ₂ - швидкості куль до удару. Швидкість ₁ малої кулі знайдемо із закону збереження механічної енергії:

звідси

(2)

(врахували, що h₁=(1-соs)).

З виражень (1) і (2 ) за умови, що ₂=0, одержимо

(3) Рис.4

Із закону збереження механічної енергії маємо

,

відкіля шукана висота

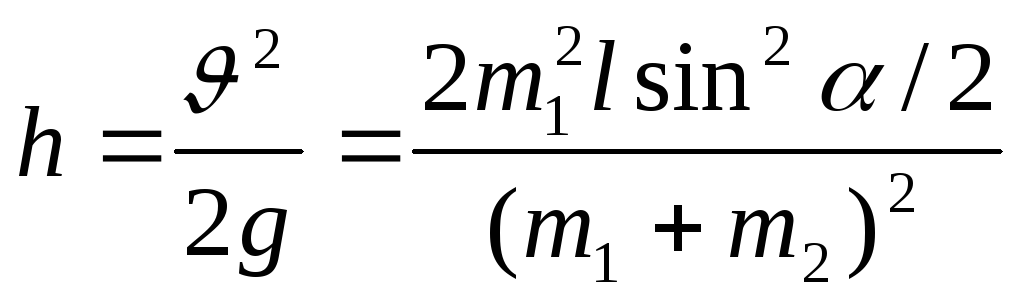
(врахували формулу (3)).

Енергія витрачена на деформацію куль при ударі,

,

чи, підставивши (2) у (4) , знаходимо

.

Перевіримо одиниці виміру обумовлених величин і проведемо обчислення.

, .

,

Відповідь:1) h=5,6 cм; 2)Т=4,12Дж.

Задача 7. Камінь, пущений по поверхні льоду зі швидкістю ₀=3м/с (рис.5), пройшов до зупинки відстань S=20,4м . Знайти коефіцієнт тертя k каменю об лід.

Дано: v=3м/с, S=20,4м.

Визначити k.

Розв’язання. Робота сили тертя при ковзанні каменю по льоду

дорівнює А=F_тр Scos, де F_тр=kmgcos, cos180 ⁰=-1, тоді

А=-kmg (1). З іншого боку, робота сили тертя дорівнює збіль-

шенню кінетичної енергії каменя А=W₂-W₁. Рис.5

Оскільки W₂=0, то А=-W₁= (2). Порівнюючи праві частини рівнянь(1) і (2), одержимо .Одиниць виміру k не має.

Підставивши числові значення й обчислюючи, одержимо:

k=

Відповідь k=0,02.

Задача 8. Хлопчик котить обруч по горизонтальній дорозі зі швидкістю v=7,2км/ч. На яку відстань s може вкотитися обруч на гірку за рахунок його кінетичної енергії? Ухил гірки дорівнює І0м на кожні І00м шляху.

Дано: v=7,2км/год=2м/с, h=10м, =100м.

Визначити S.

Розв’язання . Коло підніжжя гірки обруч мав кінетичну енергію W_k, яка складалася з кінетичної енергії поступального руху і кінетичної енергії обертання. Коли обруч вкотився на гірку на відстань s, його кінетична енергія перейшла в потенціальну.

W_k=W_п

Момент інерції обруча J=m R², частота обертання

.Тоді

.

Отже, m² = mgН , звідси . Рис.6

З (рис.6) видно, що , звідси .

Перевіримо одиниці виміру S.

.

Підставивши числові дані, одержимо:

S = Відповідь S=4,1м.

Задача 9. Олівець довжиною см, поставлений вер-

тикально, падає на стіл (рис.7). Яку кутову швидкість і

лінійну швидкість буде мати наприкінці падіння сере-

дина і верхній кінець олівця?

Дано l=0,15м.

Визначити:₁ і ₂. Рис.7

Розв’язання.

Розглянемо рух центра маси олівця . У вертикальному положені він має по-тенціальну енергію , яка при падінні переходить у кінетичну енергію обер-тання (рис.7).

- (1).

Момент інерції олівця відносно, осі що проходить через його кінець, знайдемо по теоремі Штейнера: - (2).

Підставивши (2) у (1), одержимо

, звідси

=14рад/с. Оскільки ==, а лінійна швидкість =R , то швидкість кінця олівця ₁==2,1м./с. Швидкість середини =1,05м/с.

Відповідь: ₁=2,1м/с, ₂=1,05м/с .

Задача 10. Горизонтальна платформа (рис.8) масою m=100кг обертається навколо вертикальної осі, що проходить через центр платформи, з частотою n₁=10об/хв. Людина масою m₀=60кг стоїть при цьому на краю платформи. З якою частотою n₂ почне обертатися платформа , якщо людина перейде від краю платформи до її центра? Вважати платформуоднорідним диском , а людину - точковою масою.

Дано:m=100кг, n₁=10об/хв, m₀=60кг.

Визначити n₂.

Розв’язання .

Система "людина-платформа" замкнута в проекції на

вісь у, тому що моменти сил М_mg=0 і M _mog=0 у

проєкції на цю вісь. Отже можна скористатися зако- Рис.8

ном збереження моменту імпульсу.У проєкції на вісь у:

J₁= J₂ (1)

де J₁ - момент інерції платформи з людиною, що Рис.8

стоїть на її краї, J₂ - момент інерції платформи з людиною, що стоїть в центрі, і - кутові швидкості платформи в обох випадках. Тут

- (2),

де R - радіус платформи. Підставляючи (2) у (1) і : враховуючи, що , де n-частота обертання платформи, одержимо:

; .

Обчислюючи, одержимо

Відповідь n₂=22об/хв.

Задача 11. Довести, що при малих швидкостях релятивістська формула кінетичної енергії переходить у класичну.

Розв’язання. Релятивістська формула кінетичної енергії:

Розкладемо вираз по формулі бінома Ньютона

=1 +

і відкинемо члени більш високого ступеня у силу їхньої малості (v«c). Тоді

Задача 12. Мезони космічних променів досягають поверхні Землі із самими різними швидкостями.Знайти релятивістське скорочення розмірів мезона, швидкість якого дорівнює 95% швидкості світла.

Дано v=0,95c

Визначити %.

Розв’язання.

Оскільки поперечні розміри тіла при його русі не міняються , зміна об’єму тіла визначається лоренцевим скороченням подовжнього розміру, що вира-жається формулою

Отже, об’єм тіла скорочується по аналогічній формулі

Підставляючи числові дані, одержимо

V=0,312 V₀

Тоді відносна зміна об’єму

% = 68,8%.

Задача 13. Сонце випромінює потік енергії Р = 3,9*1О²⁶ Вт. За який час масса Сонця зменшиться в 2 рази? Випромінювання Сонця вважати постійним.

Дано:Р=3,9Вт, m₀=1,989*10³⁰кг.

Визначити .

Розв’язання.

Потік енергії , випромінюваний Сонцем , визначається співвідношенням

(1).

Зміна енергії Сонця в процесі випромінювання

(2).

За умовою (3),

де m₀=1,989*10³⁰- початкова масса Сонця. Підставляючи (2) у (1), з ураху-ванням (3), одержуємо

,

Відкіля час, за який маса Сонця зменшиться в 2 рази , дорівнює

.

Перевіримо одиниці виміру обумовленої величини.

.

Підставивши числові дані й обчислюючи, одержимо

=

Відповідь =7,2*10¹²років.