2. Елементи спеціальної теорії відносності

Простір і час. Простір і час у класичній механіці. Перетворення Галілея.

Принцип відносності Галілея. Постулати спеціальної теорії відносності. Перетворення Лоренца. Відносність поняття одночасності подій. Відносність інтервалів. Лоренцеве скорочення довжини. Релятивістський закон додавання швидкостей. Інтервал між подіями і його інваріантність по відношенню до вибору інерціальної системи відліку як прояв і взаємозв'язок простору і часу.

Елементи релятивістської динаміки. Імпульс і маса в релятивістській динаміці. Основний закон релятивістської динаміки матеріальної точки. Взаємозв'язок маси й енергії. Релятивістське вираження для кінетичної енергії. Співвідношення між повною енергією і імпульсом.

Частина 1 фізичні основи механіки

§1. Кінематика матеріальної точки

Механіка – це вчення про найпростіші форми руху матерії, які полягають у переміщенні тіл одних відносно інших. Будь-який механічний рух можна розкласти на два компонента – поступальний і обертальний.

Матеріальна точка – це тіло, розмірами якого можна знехтувати в умовах даної задачі. Абсолютно тверде тіло – це тіло, деформаціями якого можна знехтувати в умовах даної задачі.

Механіка поділяється на три розділи – кінематику, динаміку і статику. Кінематика вивчає рух без урахування сил, що діють на тіло. Динаміка вивчає рух з урахуванням сил, що діють на тіло. Статика вивчає рівновагу тіл під дією прикладених до нього сил.

Швидкість. Положення матеріальної точки у просторі можна задати за допомогою радіуса-вектора , проведеного з початку координат у дану точку (див. рис.1). При цьому

r_x=x; r_y=y; r_z=z.

Рис. 1.1

Позначимо – вектор елементарного (тобто дуже малого) переміщення за елементарний проміжок часу  t,  S – елементарний шлях за проміжок  t. Вектор переміщення направлений з початкової точки у момент часуt у кінцеву в момент часу t+ t, а шлях  S – це довжина траєкторії.

Середня швидкість . (1.1)

Миттєва швидкість . (1.2)

Тобто вектор миттєвої швидкості дорівнює першій похідній від радіуса-вектора за часом і направлений по дотичній до траєкторії. Одиницею швидкості в СІ є (м/с).

Проекції швидкості на координатні осі визначаються за формулами

Модуль миттєвої швидкості дорівнює першій похідній від шляху за часом

. (1.3)

При рівномірному русі тіло проходить за рівні проміжки часу рівні шляхи, тому=сonst і визначається за формулою

=S/t. (1.4)

Обчислення пройденого шляху. Щоб визначити пройдений шлях при нерівномірному русі, потрібно розбити весь шлях на елементарні ділянки , настільки малі, що швидкостіна кожному елементарному шляху можна вважати незмінними. Тоді скориставшись формулою (1.4), отримаємо

. (1.5)

Формула (1.5) тим точніша, чим менші проміжки часу . Строгий знак рівності у (1.5) можна поставити тільки під знаком границі при:

=. (1.6)

Таким чином, щоб обчислити пройдений шлях від моменту часу до моменту часу, потрібно швидкість проінтегрувати за часом у вказаних межах. На координатній площині (V, t) пройдений шлях дорівнює площі криволінійної трапеції (див. рис.1.2).

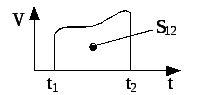
Рис.1.2

Прискорення. Якщо за час  t приріст швидкості дорівнює , то середнє прискорення визначається формулою

. (1.7)

Миттєве прискорення – це перша похідна за часом від швидкості

. (1.8)

Прискорення характеризує зміну вектора швидкості в одиницю часу. Одиницею прискорення в системі СІ є (м/с² ). При криволінійному русі вектор прискорення розкладають на дві складові – тангенціальну складову, яка направлена вздовж дотичної, і нормальну складову, яка направлена вздовж перпендикуляра до дотичної ( рис.1. 3):

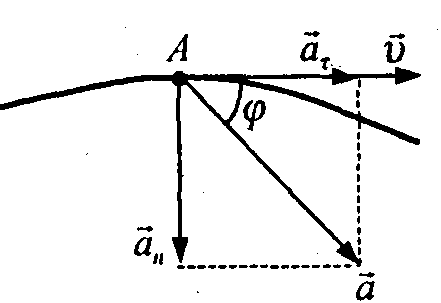
Рис.1. 3

, (1.9)

; (1.10)

; (1.11)

R – радіус кривизни траєкторії у даній точці. Тангенціальна складова (тангенціальне прискорення) визначає зміну швидкості в одиницю часу за величиною, а нормальна складова(нормальне прискорення) – за напрямком. Тоді повне прискорення

Обчислення швидкості, якщо відоме прискорення. Для рівнозмінного () руху за рівні проміжки часушвидкість змінюється на однакові прирости. Тому для цього руху прискорення

, (1.12)

де ₀ – початкова швидкість, тобто швидкість при .

При =const формула (1.6) переходить у формулу для рівнозмінного руху

; (1.13)

або в скалярному вигляді, спроектувавши вектори іна₀ , маємо

= ₀  a t, (1.14)

де знак плюс відповідає рівноприскореному рухові, а знак мінус – рівносповільненому.

Підставляючи (1.14) у (1.6), отримаємо формулу для визначення шляху при рівнозмінному русі

.(1.15)

Таким чином, формули

, ,

, .

є найбільш загальними кінематичними формулами, які справедливі для будь-якого руху.