10.3. Парабола

Парабола определяется каноническим уравнением т.е. в уравнении (1) нужно положить

К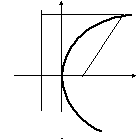оэффициентр называется К у

фокальным параметром. М

Отметим на оси Ох точку

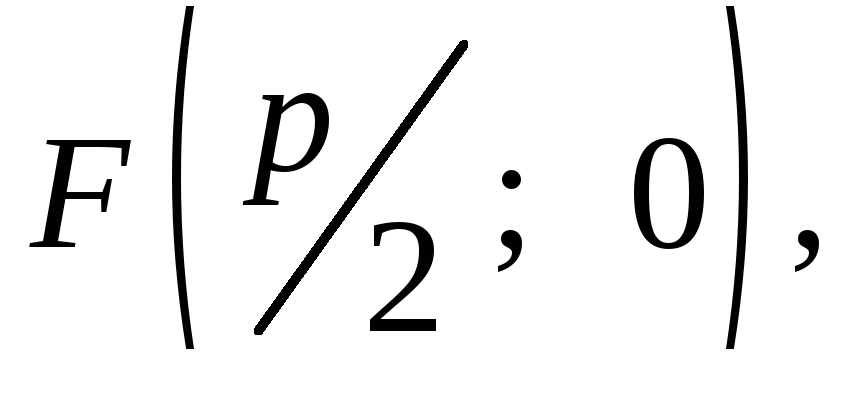называемую фокусом

параболы и проведём прямую, О F х

, называемую директрисой.

Тогда парабола может быть также определена как

геометрическое место точек, равноудалённых от фокуса и директрисы .

Действительно, для произвольной точки параболы имееми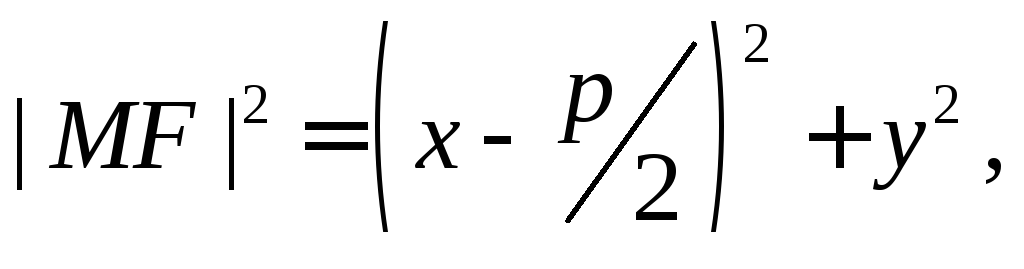откуда и следует искомое равенство

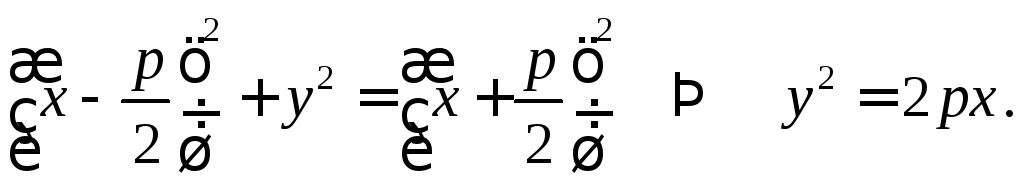
10.4. Классификация линий второго порядка

В математике доказывается следующая теорема:

Теорема. Любое уравнение вида (1), если не рассматривать случай “мнимых“ линий, путём преобразования системы координат можно привести к одному из следующих видов:

1)  эллипс;

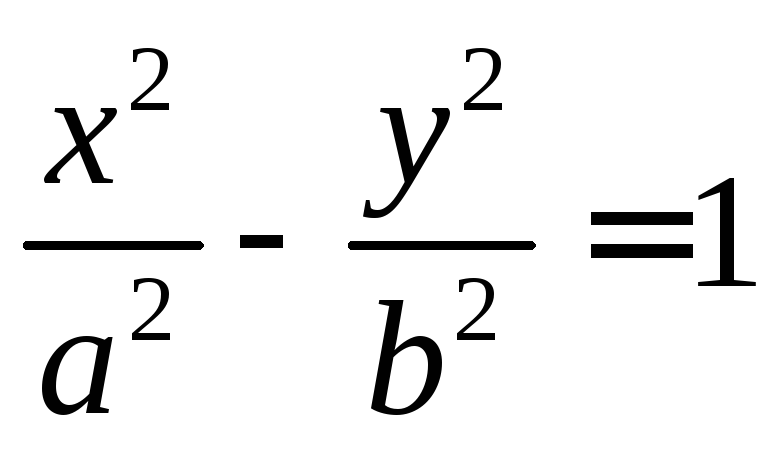
2)  гипербола;

3)  парабола;

4)  пара пересекающихся прямых;

5)  пара параллельных прямых;

6)  пара совпадающих прямых;

7)  точка.

Линии второго порядка классифицируются и по значению эксцентри-ситета:

эллипс;

парабола;

гипербола.

Лекция № 10. Тема 4 : Плоскость

4.1. Уравнение плоскости. Построение плоскости

Теорема. В ДСК в пространстве каждая плоскость может быть задана линейным уравнением и наоборот, т.е. любое линейное уравнение в ДСК в пространстве определяет плоскость.

Доказательство этой теоремы полностью аналогично доказательству теоремы о прямой линии в ДСК на плоскости.

Уравнение называетсяобщим уравнением плоскости.

Замечание 1. Аналогично следует, что вектор являетсянор-мальным вектором плоскости.

Пример 1. Составить уравнение плоскости, параллельной плоскости Оyz.

Поскольку в этом случае , то уравнение искомой плоскости будет иметь следующий вид.

Удобно и наглядно строить плоскость по её следам на координатных плоскостях, которые определяются из следующих систем уравнений:

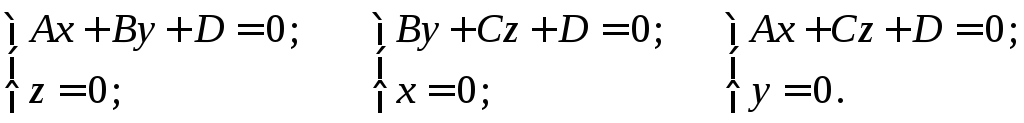
Пример 2. Построить z

плоскость, заданную общим

уравнением

Определим координаты 0 2 y

точек пересечения с осями 1

координат: (1 , 0 , 0) , (0 , 2 , 0)

и (0 , 0 , 2) и соединим эти x 2

точки отрезками.

Замечание 2. По следам плоскость удобно строить, представив уравнение плоскости в виде

Это уравнение называется уравнением плоскости в отрезках, так как  отрезки, отсекаемые плоскостью на координатных осях.

4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору

Пусть требуется составить уравнение плоскости, проходящей через точку перпендикулярно вектору. Пусть точка текущая точка плоскости. Тогда вектор , лежащий на плоскости, перпендикулярен вектору

Таким образом, из этого условия получаем

(1)

Уравнение (1) является искомым уравнением плоскости.

Пример 3. Составить уравнение плоскости, проходящей через ось

В этом случае вектор нормали к плоскости а в качестве точкивыберем начало координат. Тогда из уравнения (1) имеем