3.3. Площадь поверхности тела вращения

Пусть линия вращается вокруг осиОх.

Определим площадь

поверхности вращения.у

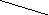
Разобьём нап

частей и впишем ломаную

в график . Тогда каждая

хордаопишетбоковую

поверхность усеченного х

конуса с площадьюО а b

.

Учитывая, что при , и переходя к пределу в интегральной сумме, получим

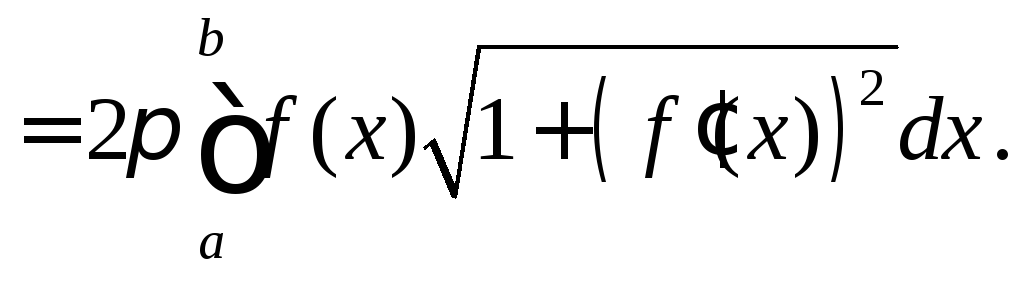(7)

Пример 6. Найти площадь поверхности сферы .

Рассмотрим сферу как поверхность, образованную вращением полу-

окружности вокруг осиОх. Тогда и по формуле (7) имеем

.

3.4. Вычисление объёма тела по площадям поперечных сечений

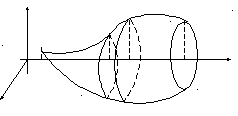Пусть нам известна площадь любого сечения тела плоскостью, перпендикулярной оси Ох: .

а b х

Составим интегральную сумму 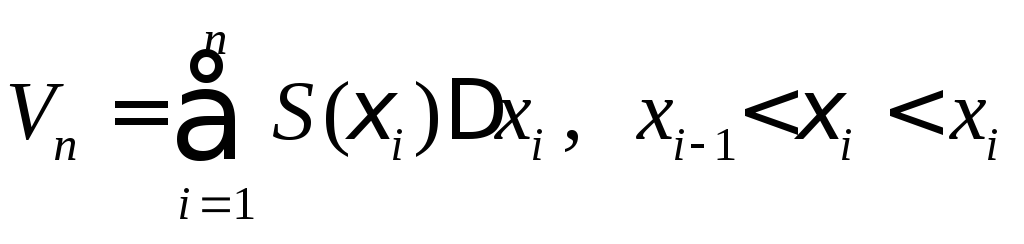. Тогда

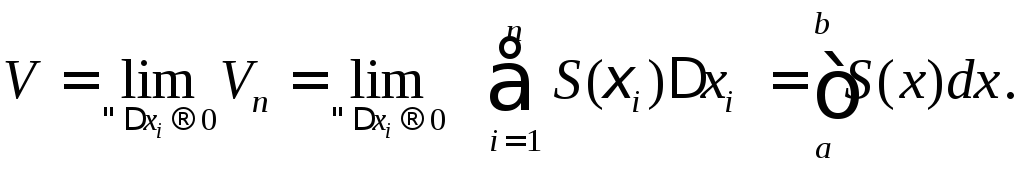(8)

Следствие. Если тело получено путём вращения криволинейной трапеции вокруг оси Ох, то из формулы (8) следует

(9)

Аналогично, если тело получено путём вращения вокруг оси Оу, то

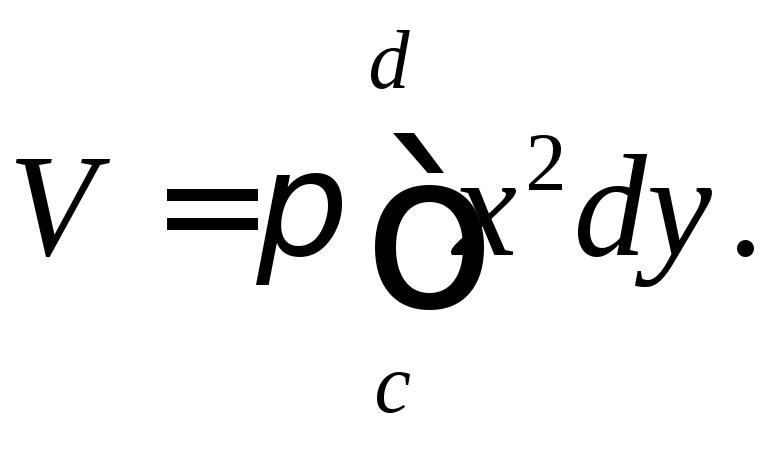
Пример 7. Найти объём шара .

Рассмотрим шар как тело, образованное вращением полукруга вокруг осиОх. Тогда по формуле (9) получаем

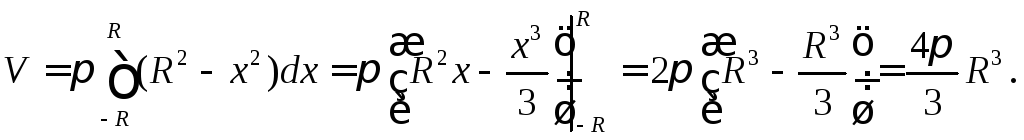
Лекция № 31

3.5. Приложения определённого интеграла к некоторым задачам физики

Приложения определённого интеграла к задачам физики рассмотрим на двух показательных примерах, решения которых представляют собой общую идею решения подобных задач.

Задача 1. Определить работу, затраченную на откачку жидкости из резервуара, имеющего форму поверхности, полученную при вращении линии

вокруг оси Оу.

у

х

Н у

О х

Работа при подъёме элементарного объёма жидкости

,

где  плотность жидкости, Н  глубина резервуара. Тогда

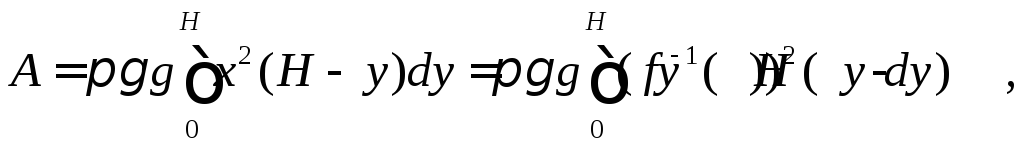
где  обратная функция к функции .

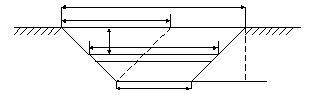
Задача 2. Определить давление жидкости на вертикальную пластину, имеющую форму равнобочной трапеции, у которой большее основание совпадает с уровнем жидкости.

а

a b

x y

xxxxxxxxxxxxxxxxxxx h

b

Давление жидкости на элементарную полоску . Из подобия треугольников определим

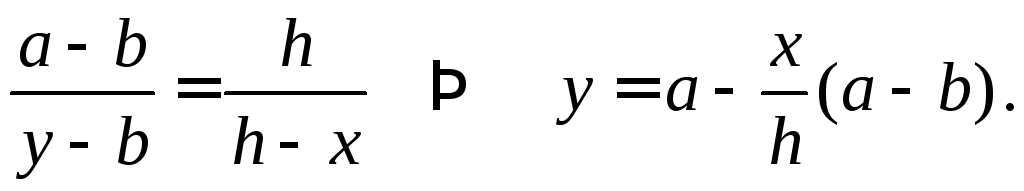
Тогда интегрируя, получаем

.

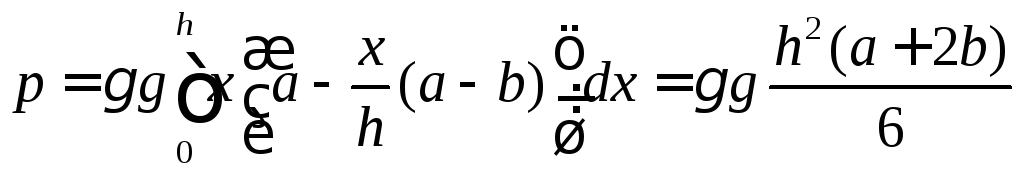Тема 4 : Несобственные интегралы

4.1. Несобственные интегралы первого рода (с бесконечными пределами)

Пусть дан интеграл с фиксированным нижним пределом интегри-рования а

.

Рассмотрим его поведение при .

Определение 1. Если существует конечный предел , то этот предел называется несобственным интегралом первого рода от функциинаи обозначается

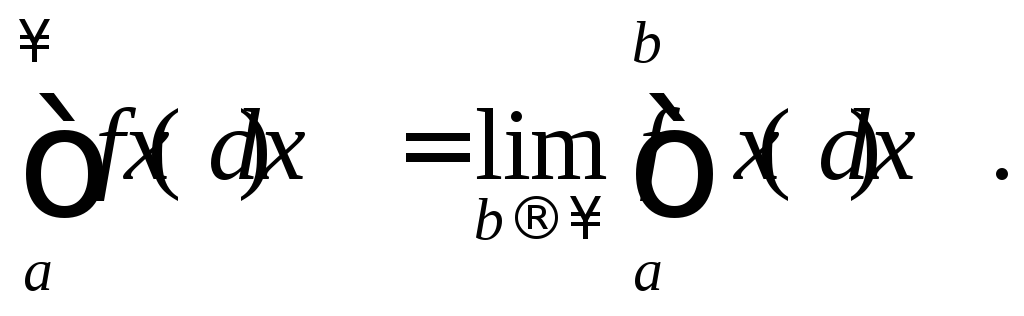(1)

В этом случае интеграл называется сходящимся. Если же предел (1) не существует или равен бесконечности, то такой интеграл называется расходящимся.

Аналогично определяются несобственные интегралы и для других бесконечных интервалов:

.

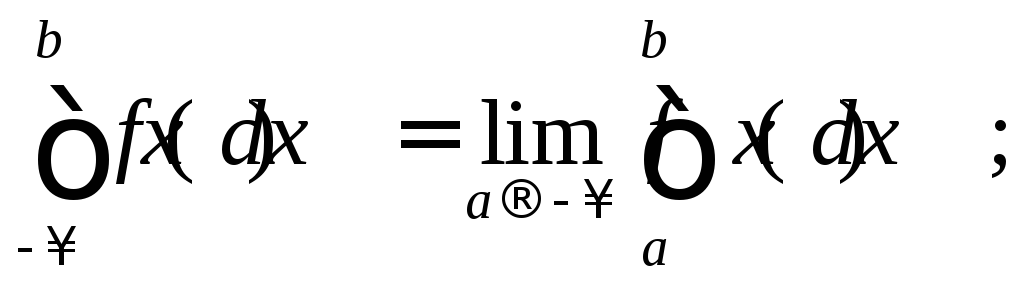
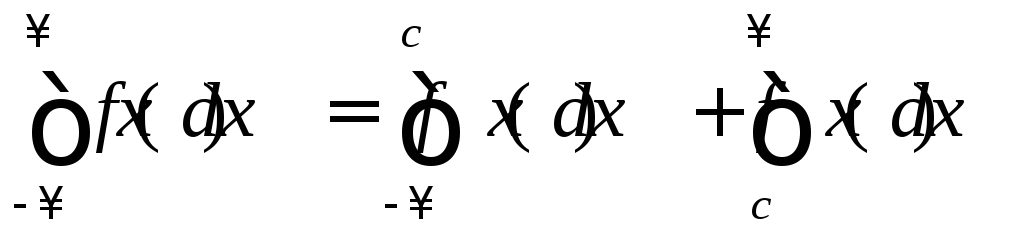Если известна первообразная функции , то

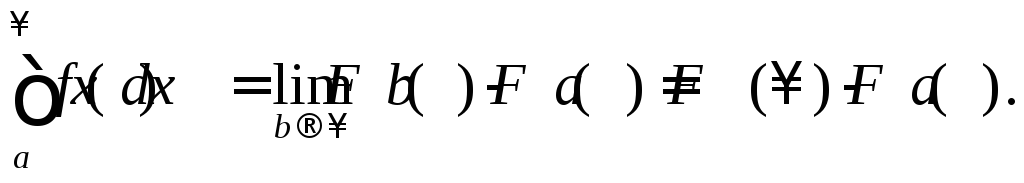(2)

Пример 1. Исследовать сходимость интеграла .

По формуле (2) получаем

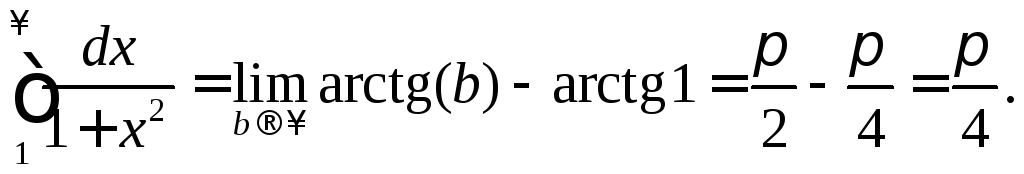
Пример 2. Исследовать сходимость интеграла

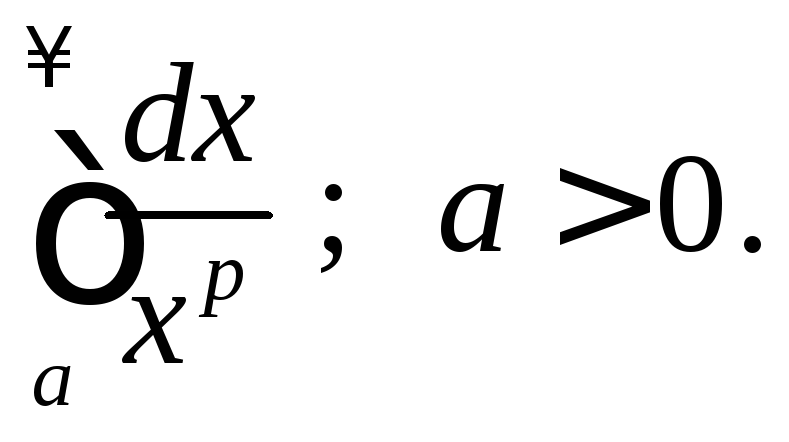
Согласно определению несобственного интеграла из таблицы неопре-делённых интегралов получим

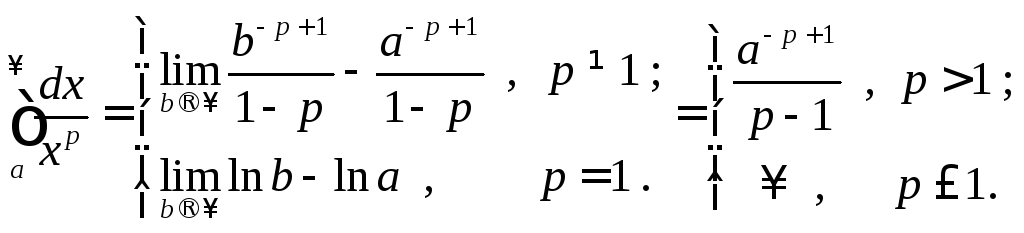
Таким образом, интеграл сходится, если степень и расходится, если.

Если первообразная функции не известна, то при исследовании несобственного интеграла на сходимость применяют признаки сравнения:

Теорема 1. Пусть , тогда

- если 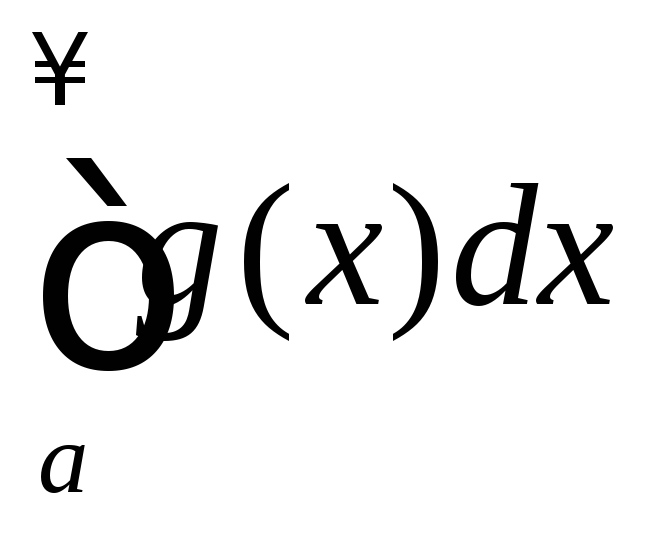сходится, то сходится и,

- если расходится, то расходится и.

В силу свойства определённого интеграла, интегрируя данное нера-венство, получаем

.

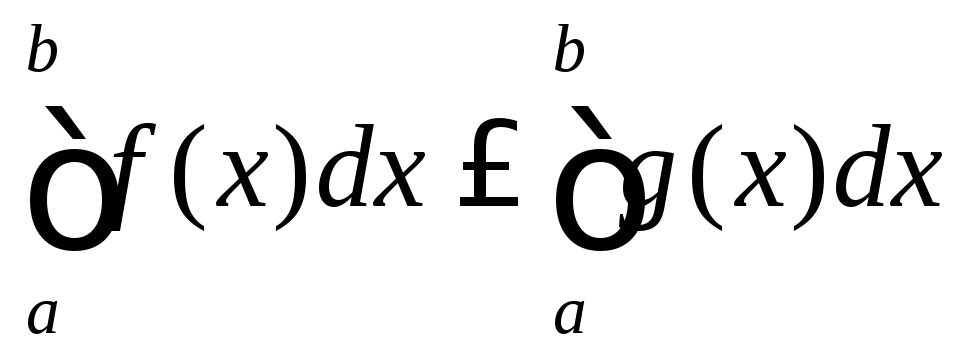Переходя к пределу при , приходим к неравенству

Аналогично доказывается вторая часть теоремы.

Пример 3. Исследовать на сходимость .

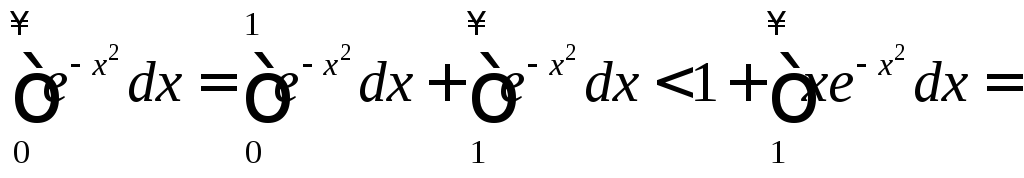
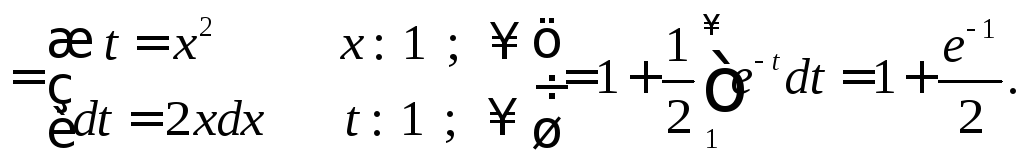
Таким образом, интеграл сходится. Неравенство было получено с использованием свойства 7 об оценке интеграла.

Теорема 2. Если .

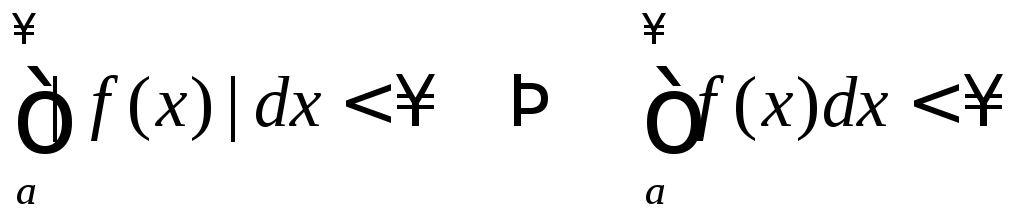Доказательство аналогичное.

В этом случае интеграл 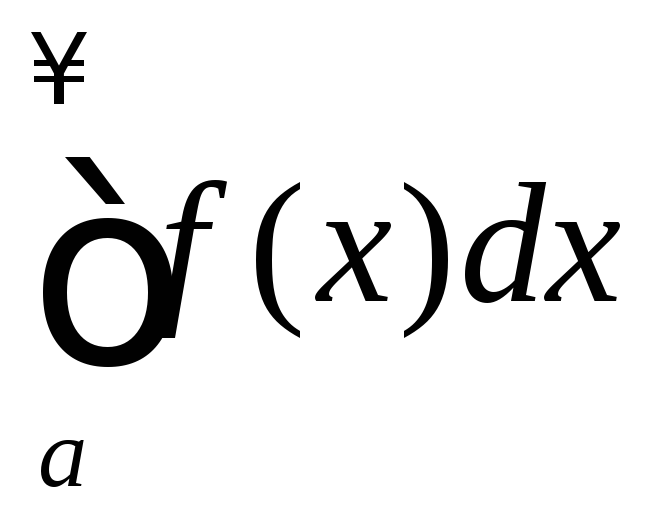называетсяабсолютно сходящимся. Если 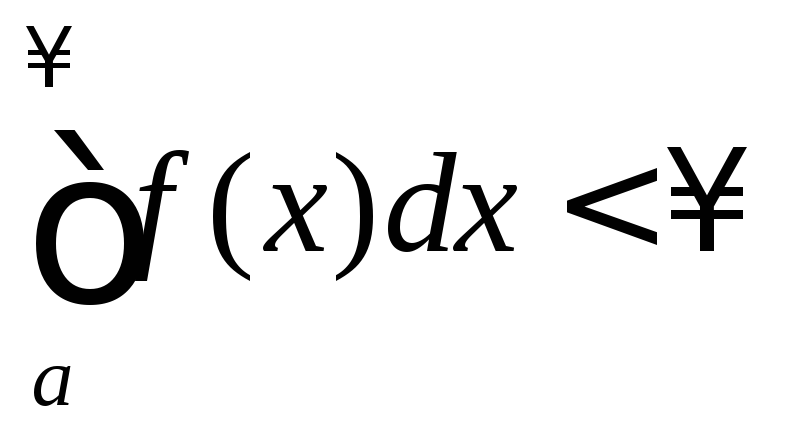, а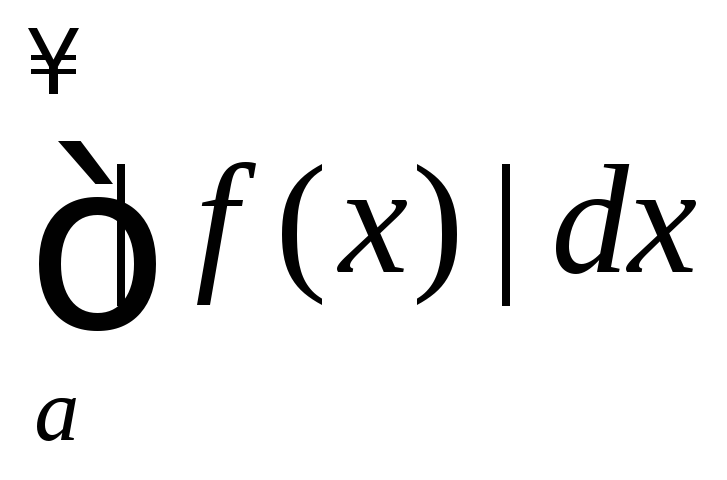расходится, то интеграл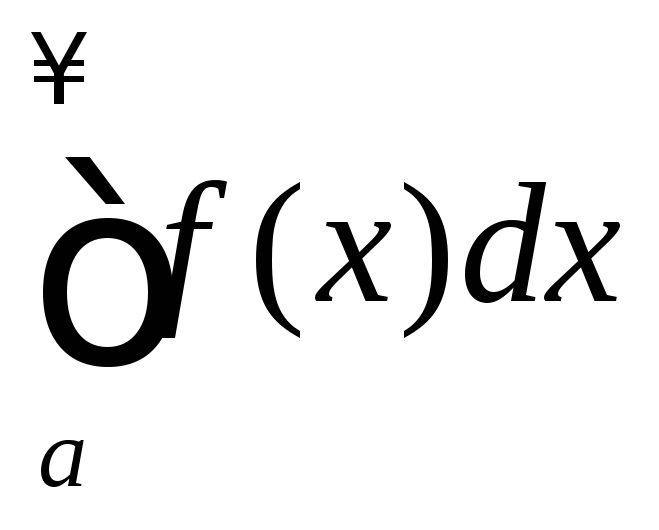называетсяусловно сходящимся.

Например, интеграл является абсолютно сходящимся, так как

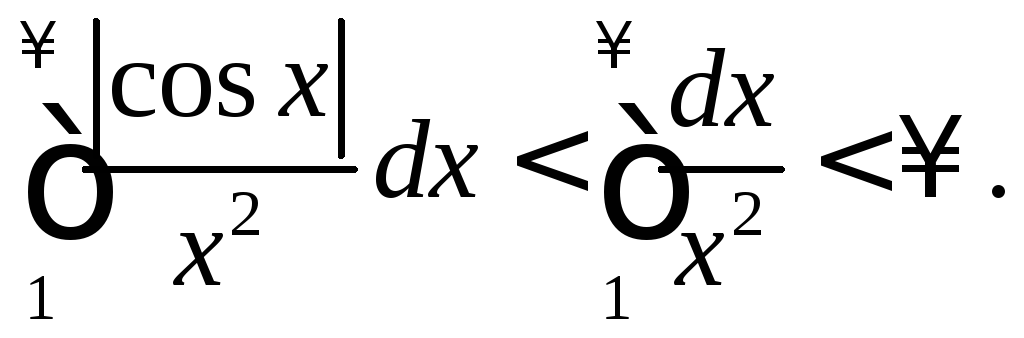
Интеграл  условно сходящийся.