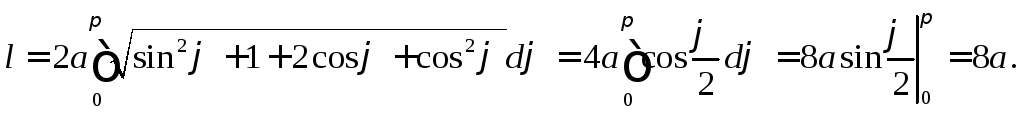2.7. Интегрирование по частям в определённом интеграле

Если соответствующие интегралы существуют, то проинтегрируем от а до b формулу

.

Получим формулу интегрирования по частям

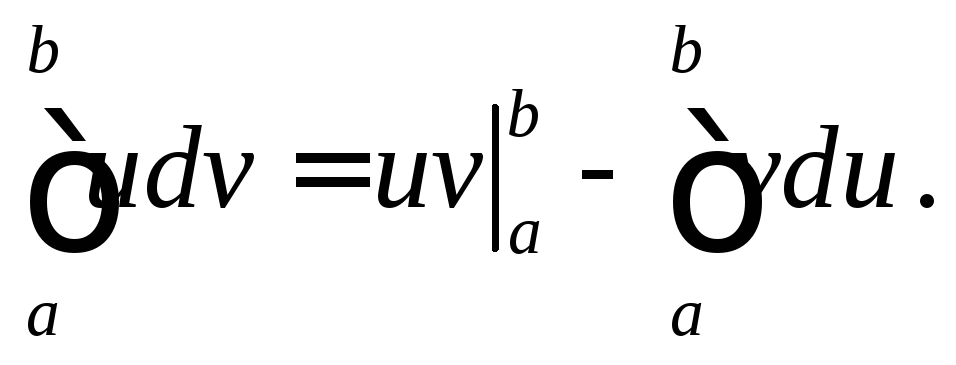(3)

Замечание 4. Выражения для и и выбираются из таких соображе-ний, чтобы интеграл в правой части формулы (3) был известен.

Пример 5.

.

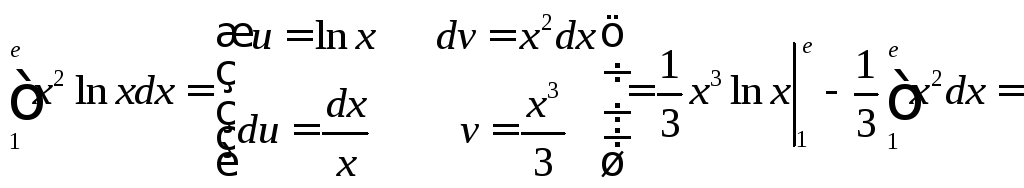
Аналогично, как и для неопределённого интеграла, формулу интегрирования по частям можно применять для вычисления интеграла неоднократно.

Пример 6.

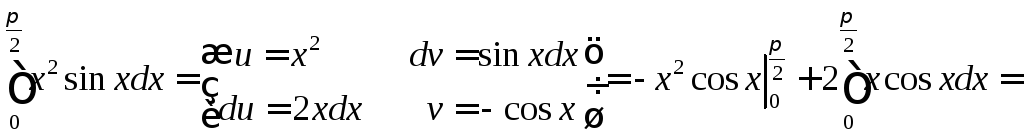
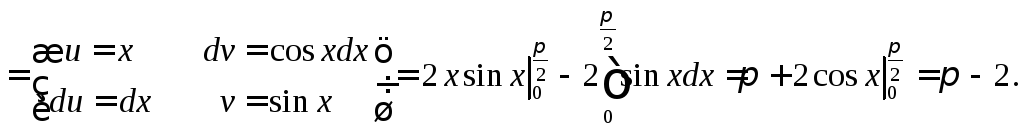
Лекция № 30. Тема 3 : Приложения определённого интеграла

3.1. Площадь плоской фигуры

3.1.1. Площадь фигуры в ДСК.

Как известно, площадь криволинейной трапеции , если. Если же  знакопеременная функция, то

де

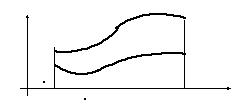
В случае, если плоская фигура ограничена сверху кривой , а снизу – кривой, то

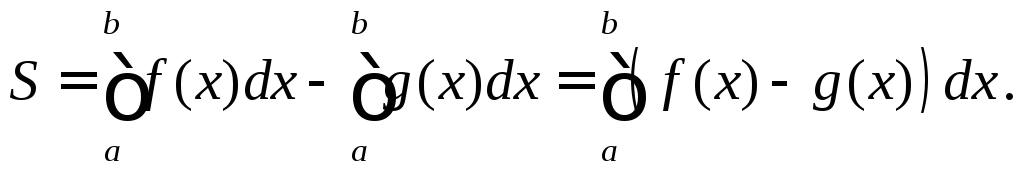
у

x

О а b

3.1.2. Площадь фигуры, если ее граница задана параметрическими уравнениями.

Пусть для криволинейной трапеции линия задана параметрическими уравнениями: 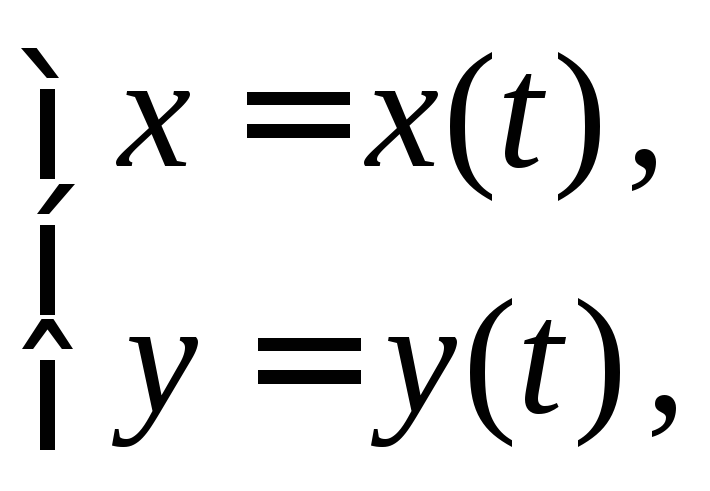при этом . Тогда, делая замену в интеграле, получаем

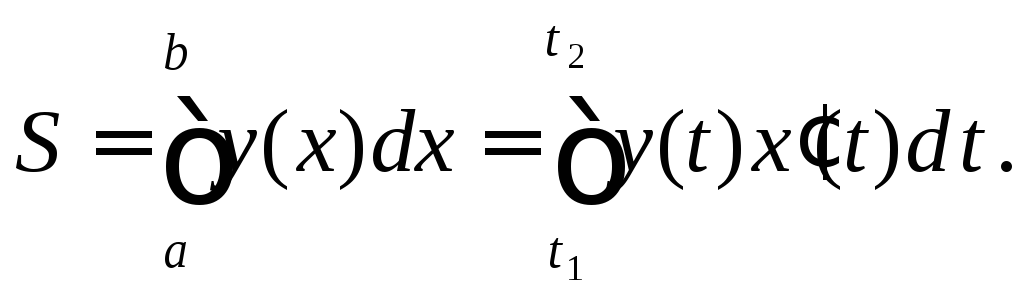(1)

Пример 1. Найти площадь эллипса .

Запишем параметрические уравнения эллипса 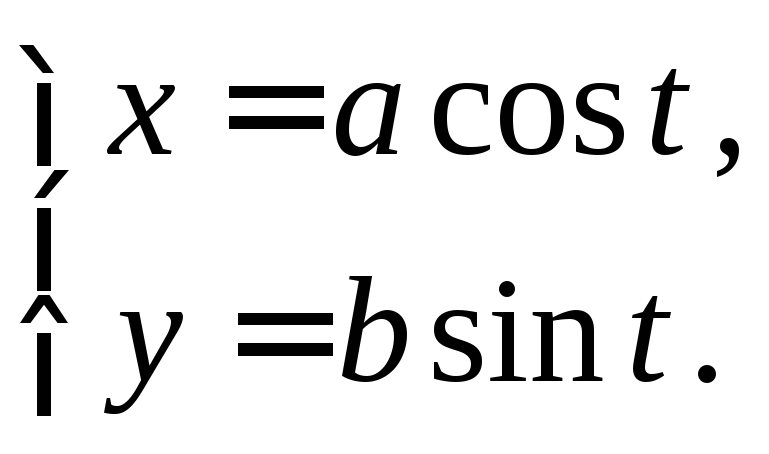Тогда по формуле (1) в силу симметрии получим

3.1.3. Площадь в полярной системе координат

(площадь криволинейного сектора).

Рассмотрим фигуру, ограниченную двумя

лучами: , выходящими из полюса

и кривую . Определим её площадь.

Для этого разобьём её на п секторов с О P

площадью

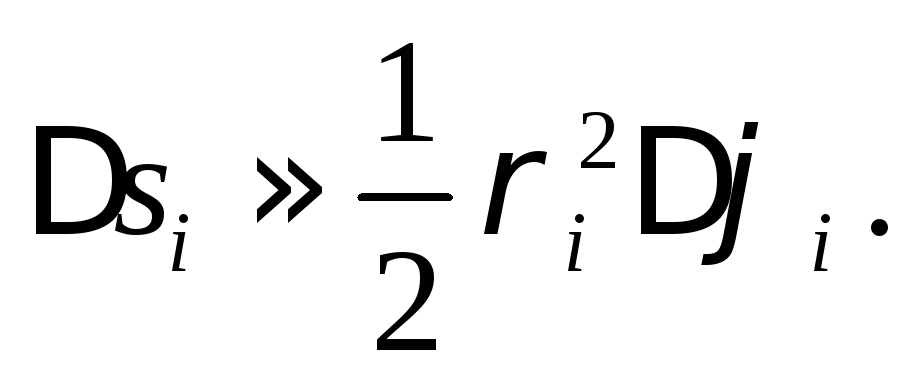
Составим интегральную сумму

, (2)

где .

Переходя к пределу в формуле (2) при , имеем

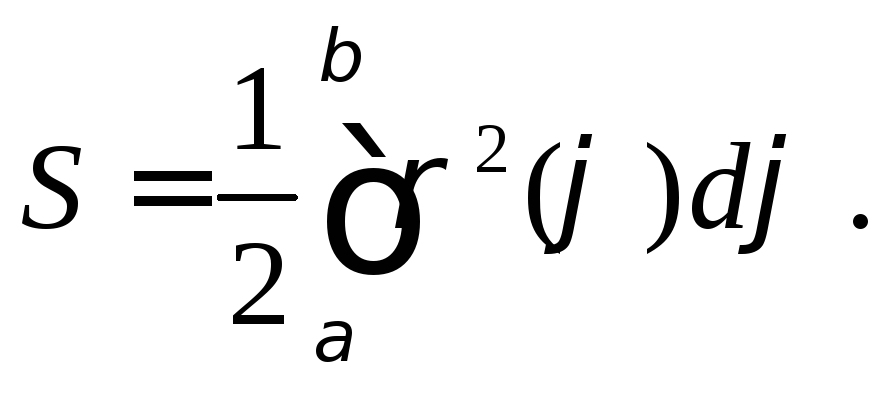(3)

Пример 2. Найти площадь кардиоиды

В силу симметрии, с учетом формулы (3),

получаем

а

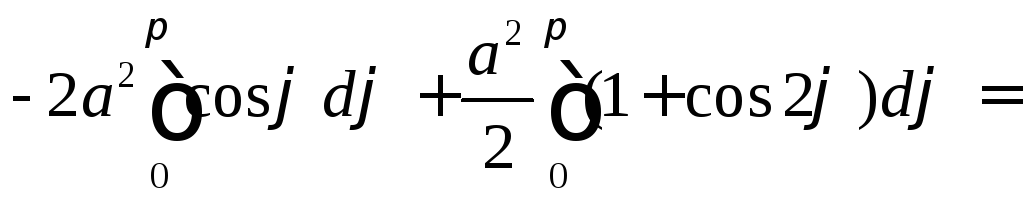2а О

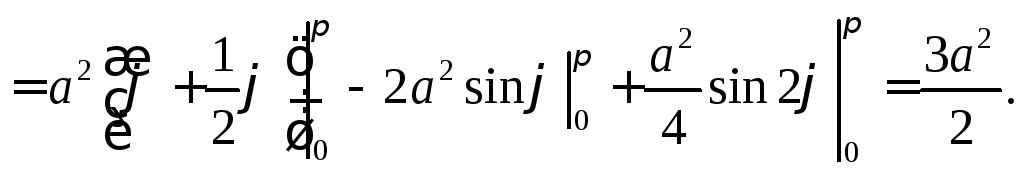
3.2. Длина дуги плоской кривой

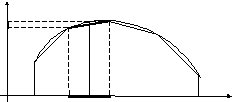
3.2.1. Кривая задана в ДСК.

Определим длину дуги АВ. Впишем в неё ломаную, длина которой

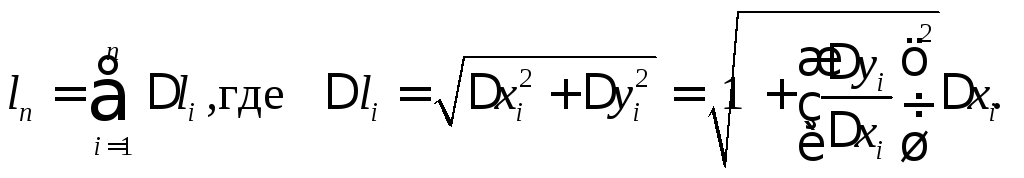
у

х

О а b

Воспользуемся теоремой Лагранжа: , где. Тогда

. (4)

Пример 3. Найти длину дуги линии при.

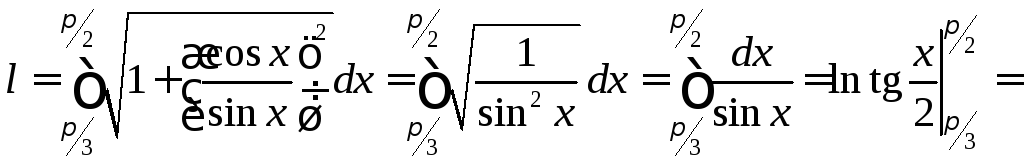
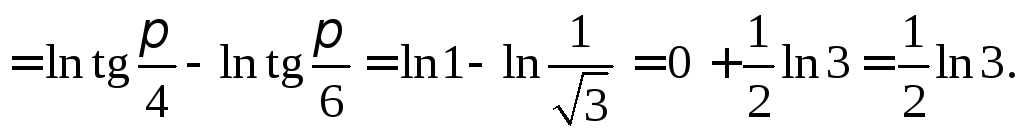
3.2.2. Линия задана параметрическими уравнениями.

Линия задана уравнениями и пусть. Тогда, заменяя переменную в интеграле (4), с учетом значе-ния производной от функции, заданной параметрическими уравнениями,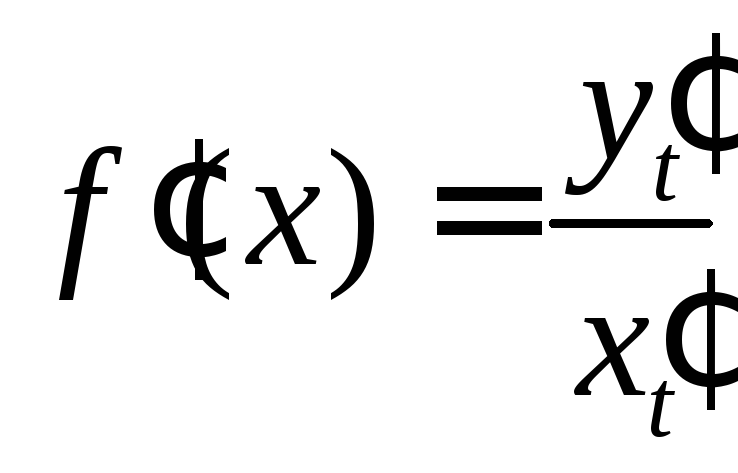из формулы (4) следует

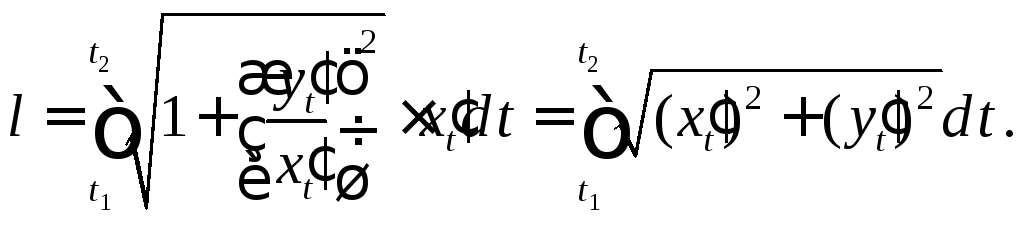(5)

Замечание. Выражения назы-ваются дифференциалами дуги.

Пример 4. Найти длину развертки окружности

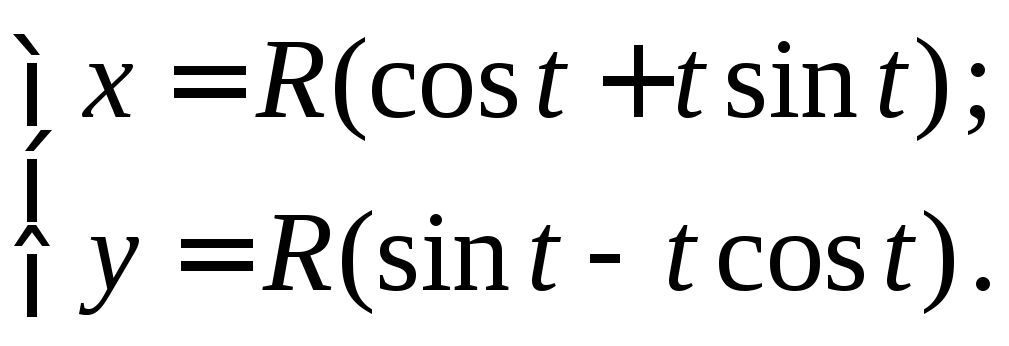
Согласно формуле (5) получаем

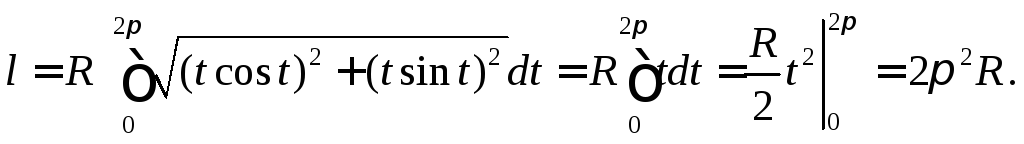
3.2.3. Линия задана в полярной системе координат.

Рассматривая как параметр с учетом, что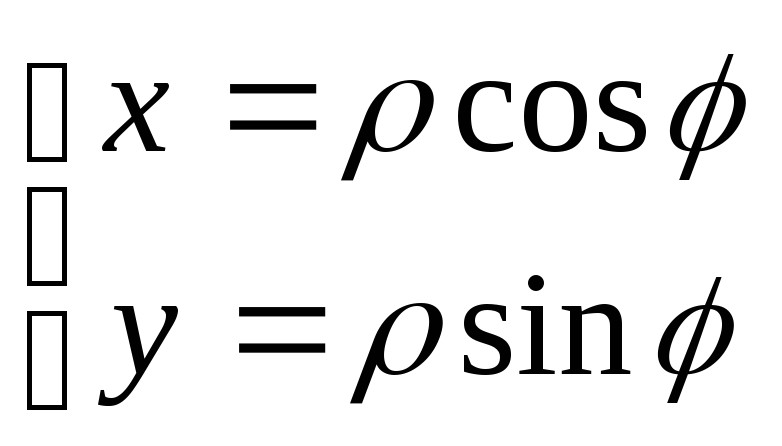и, получаем

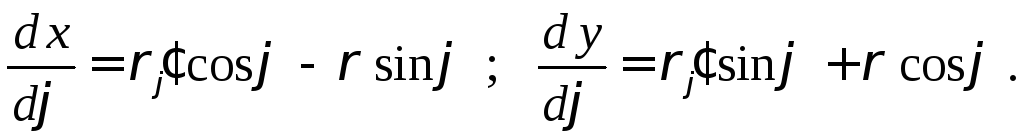
Тогда из формулы следует

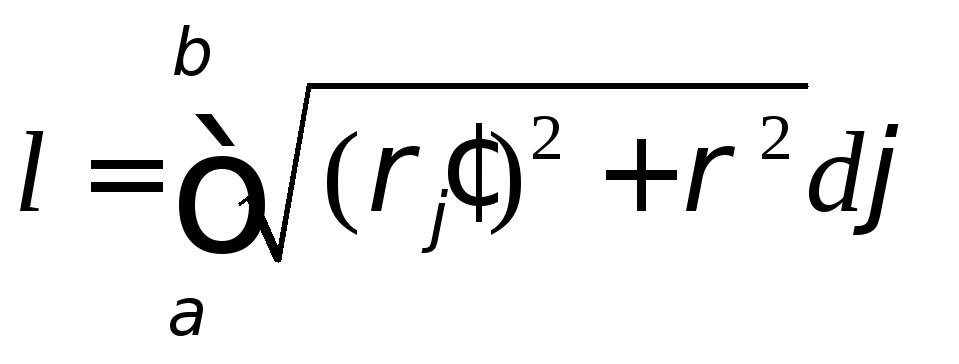. (6)

Пример 5. Найти длину кардиоиды .

В силу симметрии по формуле (6) получаем