15. Имеет ли диофантово уравнение

всегда целые решения?

Решение. Для взаимно простых чисел a и b наибольшим общим кратным будет 1. Поэтому нахождение решения (x₀, y₀) этой задачи сводится к применению алгоритма Эвклида, определяющего наибольшее общее кратное. (Он же определяет наибольший отрезок, откладывающийся целое число раз в двух неравных, соизмеримых, отрезках.)

16. Отыскание какого-либо частного решения диофантова уравнения

может вызвать определенные трудности, особенно когда коэффициенты a, b и c достаточно велики по абсолютной величине. Попробуйте предложить какой-либо способ их отыскания. В математике известны несколько таких способов.

Замечание 1: Всегда применим алгоритм Эвклида для нахождения решения (x₀,y₀) уравнения , как в предыдущей задаче, и переход к решению (x, y) = (сx₀, сy₀) уравнения , как в задаче № 14.

Замечание 2: Алгоритм Эвклида определяет наибольший общий делитель, который для двух взаимно простых чисел равен 1. По алгоритму Эвклида из большего числа, a или b, вычитают меньшее число, b или a, столько раз, чтобы остаток был меньше меньшего из чисел. Затем первый остаток вычитают из меньшего числа столько раз, чтобы второй остаток стал меньше первого, затем второй остаток вычитают из первого остатка столько раз, чтобы третий остаток стал меньше второго и т.д. Последний остаток равен 1. Итоговое тождество с 1 в остатке получается после соответствующего числа сложения и вычитания коэффициентов a и b. Приведение подобных в этом тождестве даёт численные коэффициенты при a и b, которые равны решению x₀ и y₀. уравнения .

Решим, например, уравнение . Числа 3 и 11 взаимно простые. Применим алгоритм Эвклида:

Отсюда следует, что x = 4 и y = -1.

17. Составьте какие-либо практические задачи, которые сводились бы к диофантову уравнению

_.

18. Известны ли вам какие-либо проблемы, приводящие к диофантовым уравнениям порядка выше первого?

19. Могут ли числа 8,9,10 быть членами одной и той же геометрической прогрессии?

20. Доказать, что сумма произведения четырех последовательных натуральных чисел и единицы есть точный квадрат.

Решение. Проводим очевидные преобразования:

.

21. Доказать, что если все стороны прямоугольного треугольника выражаются целыми числами, то одно из них или все три числа четные, а нечетных чисел может быть только два.

Замечание: Простой способ доказательства сводится к применению теоремы Пифагора.

22. Доказать, что квадрат всякого нечетного числа, уменьшенный на единицу, делится на 8.

Действительно: из и из чет­ности числаверно

23. Доказать, что разность квадратов двух нечетных чисел делится на 8. (См. предыдущий пример).

24. Доказать, что сумма двух последовательных степеней числа 2 делится на 6.

25. Имеют ли точную верхнюю и нижнюю грани:

а) множество площадей многоугольников, описанных около круга радиуса r ?

б) множество площадей многоугольников, вписанных в круг радиуса r ?

в) множество значений температуры материальных объектов?

г) множество значений скоростей в природе?

Интерпретируйте понятия точной верхней и нижней граней применительно к данным геометрическим и физическим образам.

Определение точной верхней (нижней) грани дано в лекции МНОЖЕСТВА в разделе числовые множества ниже аксиомы полноты.

26. Покажите, что сумма рационального и иррационального числа не может быть рациональным числом, доказав предварительно, что сумма и разность двух рациональных чисел есть число рациональное.

27. Доказать, что если корень целой степени из целого положительного числа не есть целое число, то он не может быть и дробным.

28. Доказать, что если квадратное уравнение с рациональными коэффициентами имеет иррациональный корень , то второй корень будет также иррациональным и сопряженным первому, то есть.

Решение. По условию задачи коэффициенты квадратного уравнения рациональны. Сумма и произведение его корней, выражающихся через эти коэффициенты, как следует из теоремы Виета, также должны быть рациональны. Сумма и произведение двух выражений, из которых одно иррационально, могут быть рациональными только в том случае, если второе выражение тоже иррационально и сопряжено первому, так как

– рациональное выражение и

–также рационально.

29. Доказать, что если в уравнении

коэффициенты p и q рациональны и связаны соотношением:

где – тоже рациональное число, то его корни всегда рациональны.

Подсказка: покажите, что в этом случае .

30. Доказать, что если квадратное уравнение

где р и q – целые числа, имеет рациональные корни, то эти корни могут быть только целыми числами.

31. Доказать, что при действительных положительных a и b

Подсказка: Возведение левой и правой частей неравенства в квадрат и приведение подобных даёт неравенство , которое верно. При условиях задачи это преобразование обратимо!

32. Доказать, что cумма квадратов двух нечeтных чисел не может быть квадратом целого числа. (Имеет 1 элементарный множитель 2 ?)

33. Доказать:

34. Учитель Н.Нестеренко из Луганской области обнаружил, что существуют 2n -значные натуральные числа, равные сумме квадратов своих n-значных частей:

Найдите (можно и с помощью ЭВМ) натуральные числа, обладающие этими свойствами.

Н.Нестеренко утверждает, что таких чисел бесконечно много. Так ли это?

Множество действительных чисел несчетно. Множество действительных чисел мы связываем с числовой прямой. Поэтому для доказательства этого утверждения достаточно установить взаимно однозначное соответствие между точками интервала и числовой прямой, поскольку несчетность множества, задаваемого интервалом , уже доказана.

Рассмотрим прямоугольник aABb (см. рис. 7.11). Выберем произвольно точку и точку . Проведем прямые AO₁ и BO₁. Пусть – произвольная точка интервала (a, b), лежащая правее O₁. Для отыскания соответствующей ей точки W на прямой l строим и проводим прямую O₂K, пересекающую l в точке W (если точка лежит левее O₁, то построения аналогичны).

Рис. 7.11. Взаимно однозначное соответствие между точками интервала (a, b) и числовой

прямой l.

Интересно, что точка  – основание перпендикуляра к прямой l – окажется при таком соответствии неподвижной, то есть переходит сама в себя.

Есть мнение: “Беско-нечность - это место, где происходит то, чего не бывает”.

Легко убедиться, что это соответствие взаимно однозначно. Отсюда следует, что и прямая l, и интервал (a,b), как и отрезок [0;1], имеют мощность континуума. Удивительный факт: на всей прямой не больше точек, чем на отрезке [0;1]!Этот эффект порожден свойствами бесконечных множеств.

Рис. 7.12. Возможный способ установления взаимно однозначного соответствия между точками интервала (a, b) и числовой прямой.

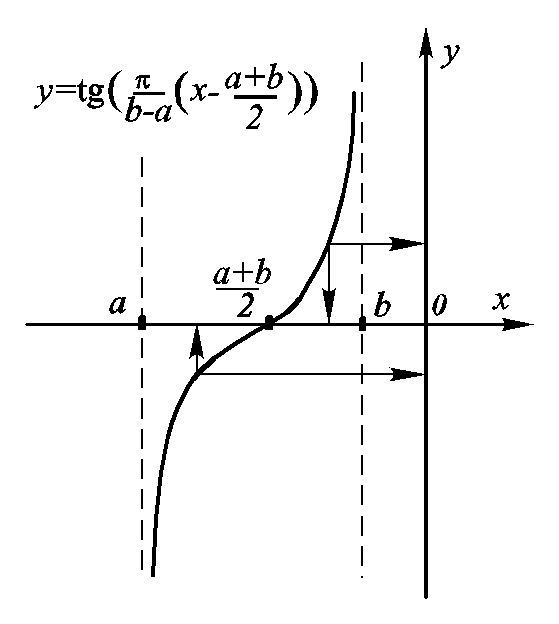
Взаимно однозначное соответствие между точками х интервала (a, b) и точками прямой можно установить и аналитически. Например, функция устанавливает такое соответствие. При этом интервал (a, b)лежит в области определения функции, а областью изменения функции является вся осьy(рис. 7.12).

Таким образом, мы доказали, что множество действительных чисел несчетно. Из несчетности множества действительных чисел следует важный факт: множество иррациональных чисел также несчетно.

Действительно, если предположить противное, т.е. что множество иррациональных чисел счетно, то в объединении со счетным множеством рациональных чисел получим множество действительных чисел, и оно окажется счетным, что противоречит доказанному (Кантором).

35. Найдите другие геометрические и аналитические способы доказательства эквивалентности точек прямой и интервала (a, b).

257