10. В условиях предыдущей задачи укажите, что представляет собой множество , и найдите число его членов.

Решение. Множество – это множество туристов не посетивших художественную галерею и/или Кунгурскую ледяную пещеру. Из задачи № 9: , и . Поформуле, применённой в № 6, получаем

11. 80% учащихся лицея ценят классическую музыку, 75% - стремятся ее понять, 55% - посещают симфонические концерты. Каким может быть наименьшее количество лицеистов, которые и ценят классическую музыку, и стремятся ее понять, и посещают симфонические концерты? Каков может быть наибольший процент лицеистов, никак не соприкасающихся с этим духовным богатством?

12. Как связаны между собой множество треугольников, у которых две биссектрисы равны между собой, с множеством треугольников, у которых две медианы равны между собой, и множеством равносторонних треугольников?

Подсказка решения. Пусть А – множество треугольников, у которых две биссектрисы равны между собой, B – множество треугольников, у которых две медианы равны между собой, С – множество равносторонних треугольников. Если Вы докажете, что и из равенства биссектрис, и из равенства медиан следует равенство боковых сторон треугольника, то очевидными станут следующие заключения: А = B – множество равнобедренных треугольников и А = B  С.

13. Можно ли разменять 200 долларов купюрами по 5, 10 и 20 долларов так, чтобы всего было 20 купюр?

Решение. Предположим, что такой размен возможен. Для этого потребуется x купюр по 5 долларов, y - по 10 долларов и - по 20 долларов. Тогда

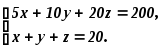
Мы получили систему двух линейных алгебраических уравнений с тремя неизвестными. На множестве действительных чисел она может иметь либо бесчисленное множество решений, либо не иметь решений. Нас интересуют решения на множестве натуральных чисел. Ситуация поэтому может быть иной.

Решим систему

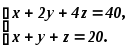
Вычитая из первого уравнения второе, получим:

Методом подбора находим семь возможных для данной задачи значений от 0 до 6, которые позволяют получить семь наборов решений:

Таким образом, 200 долларов можно разменять семью способами купюрами по 5, 10 и 20 долларов с общим числом купюр 20.

Изменим условие задачи незначительно: возможно ли разменять 200 долларов 20 купюрами номиналом 5, 20 и 50 долларов?

Аналогично предыдущему, для решения задачи получаем систему

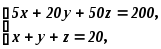
где x - число купюр номиналом 5 долларов, y - 20 долларов и - 50 долларов. Преобразуя ее, получим:

Попытки подобрать значения y и , удовлетворяющие этому уравнению, результата не дают. Его простейший анализ показывает, что при любых отличных одновременно от нуля y и левая часть уравнения должна делиться на 3, но правая часть не делится на 3 нацело. Стоит, однако, уменьшить общее число купюр, предназначенных для размена, с 20 до 19 штук, задача вновь окажется решаемой. Она сведется к системе

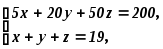
которая преобразуется в уравнение

или

,

откуда находим три набора решений:

Уравнение

рассматриваемое на множестве целых чисел, на протяжении многих столетий привлекало внимание ученых, как с точки зрения практических приложений, так и с позиций анализа интересных математических идей, которые легли в основу важного научного направления – диофантова анализа. Именно Диофант – греческий математик из Александрии, живший в III веке до нашей эры, оставил потомкам свой труд, ставший основой теории чисел. И хотя методы решения данного уравнения были уже известны в XII в. до н. э. индийскому математику Бхаскару, строгой научной теории для исследования подобных уравнений (не обязательно первого порядка) не существовало.

Имеет место важная теорема, определяющая необходимое и достаточное условие существования решения диофантовых уравнений первого порядка, называемых еще неопределенными.

ТЕОРЕМА.Уравнение гдеa, b иc – целые числа, имеет целые решения для неизвестных x и y тогда и только тогда, когда правая часть делится на число d – наибольший общий делитель коэффициентов a и b. Все возможные решения этого уравнения задаются формулами:

где x₀, y₀ – какое-то одно целое решение данного уравнения, а параметр t – целое число.

При любом целом t мы будем получать некоторое решение данного уравнения (в этом легко убедиться непосредственной проверкой).

Теперь становятся понятными ситуации с возможностью размена некоторой суммы денег купюрами определенного номинала, общее число которых задано.

14. Если числа a и b взаимно простые, то диофантово уравнение

всегда имеет целое решение. Докажите этот факт.

Доказательство. Из двух взаимно простых чисел a и b одно обязательно нечётное. Почему? Тогда, если при этих условиях имеет решение (x₀, y₀) диофантово уравнение следующей задачи, то для уравнения решением будет: (x, y) = (сx₀, сy₀).