Бесконечными множествами.

Это означает, что бесконечные множества AиBэквивалентны,A̴B, имеют «одинаковую мощность». Интересно, что при этом множествоA эквивалентно своему подмножествуB,A B, так как квадраты натуральных чисел–числа натуральные. Такая эквивалентность для них возможна потому, что оба множества бесконечны.

Рис. 7.6. Установление взаимно однозначного соответствия между равными сторонами равнобедренного треугольника.

2. ПустьLMиNM–равные стороны равнобедренного треугольникаLMN (рис. 7.6).

Связав точки АиВравных сторон треугольника отрезками прямых, параллельных основаниюLN, получим взаимно однозначное соответствие между точками множеств, определяемых отрезкамиLM иNM. Следовательно, эти множества эквивалентны и имеют одинаковую мощность.

3. Пусть теперь LN и МN – неравные стороны треугольника LMN (рис. 7.7). Связав точки А и В на этих сторонах отрезками прямых, параллельных стороне LM, получим, что и неравные между собой стороны определяют множества точек одинаковой мощности. Дело в

Рис. 7.7. Установление взаимно однозначного соответствия между неравными сторонами равнобедренного треугольника.

том, что стороныLNиMNимеют разную длину, но каждая из них содержит бесконечное множество точек, которых одинаково “много”.

Счетные множества

Множество назовем СЧЕТНЫМ, если оно эквивалентно множеству натуральных чисел.

Таким образом, возможность «пронумеровать» все элементы множества определяет его счетность. Эта задача далеко не всегда решается просто.

Отметим некоторые свойства счетных множеств.

1. Из всякого бесконечного множества всегда можно выделить счетное множество.

Действительно, если множество Aбесконечно, то счетное множествоNможно построить следующим образом. Выделим в качестве первого элемента множестваN, например, элементмножестваA.Так какAбесконечно, то исключение из него одного элементасохранит его бесконечность. Далее отделим от оставшегося множества элемент,присоединив его к множеству N, потом из бесконечного множества 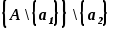отделим элемент , присоединив егокN,и так далее. МножествоN примет вид: и будет счетным.

Приведите пример, иллюстрирующий это свойство.

2. Всякое бесконечное подмножество счетного множества тоже счетно.

Если множество A счетно, а B – его бесконечное подмножество, то, перебирая последовательно элементы множества A, мы будем встречать элементы множества B и, нумеруя их, то есть элементы множества B, B A, получим бесконечное счетное множество.

3. Объединение любого конечного или счетного множества счетных множеств есть счетное множество.

Для доказательства этого свойства рассмотрим счетные множества:

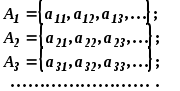
Сформируем из этих множеств новое множество

Оно образуется так, что вначале располагается элемент , затем идут элементы, у которых сумма индексов равна3, потом4, и так далее. Такое множество охватывает все элементы множестви само является счетным, эквивалентнымN.

Мощность континуума

Рассматривая свойства счетных множеств, мы стремились доказать счетность тех или иных бесконечных множеств. Однако все ли бесконечные множества счетны? Чтобы обнаружить несчетные множества, пришлось преодолеть немало трудностей. И Б. Больцано, и Г. Кантор, чувствуя, что идея установления взаимно однозначного соответствия есть ключ к поиску мощности бесконечных множеств, были близки к решению вопроса одновременно. Б. Больцано первым пришел к способу оценки бесконечных множеств путем установления взаимно однозначного соответствия, а Г. Кантор первым сумел найти несчетное множество. Оно бесконечно и не эквивалентно множеству натуральных чисел.

ТЕОРЕМА. Отрезок числовой прямой содержит несчетное множество точек.

ДОКАЗАТЕЛЬСТВО.

(Другой способ доказательства этой теоремы, «диагональный метод Кантора», приведен в дополнении)

Предположим противное: –счетное множество точек. Пронумеруем их:

Любая ли точка этого отрезка оказывается включенной в данную последовательность?

Для доказательства теоремы следует найти такую точку на отрезке , которая не охватывается данной последовательностью.

Для этого разделим отрезок на три равные части (рис. 7.8). Получим отрезки:

Рис. 7.8. Построение точки, не входящей в последовательность .

Почему делим на 3 части, а не пополам или же на 4 части? Почему эти 3 части должны быть равны?

Хотя бы на одном из них нет точки_. Выделив его, делим новый отрезок, являющийся подмножеством отрезка , снова на три равные части и выделим ту, на которой нет точки(на этой“трети”не будет и точки , и точки , как это было установлено выше). Далее новый отрезок опять делим на три равные части и выбираем ту из них, где нет точкиа₃(как показано, точек ина ней также не будет), и так далее. В результате наn-м шаге мы получаем отрезок длины , на котором также нет точек,,,...,.Продолжая бесконечно этот процесс, мы находим точкуа, которая не включена в последовательность

Действительно, а – общая точка этих отрезков. Будучи точкой отрезка , она должна входить в указанную последовательность,но это невозможно, потому что, какое бы n мы ни взяли, точка а_n не может принадлежать соответствующему отрезку, а точка а будет ему принадлежать, следовательно, а отлична от всех а_n, что и доказывает теорему.

Мощность множеств, эквивалентных отрезку , назовемМОЩНОСТЬЮ КОНТИНУУМАи обозначим буквойc.

Укажем некоторые из таких множеств.

Рассмотрим отрезок . Записанная ниже формула

,

устанавливает взаимно однозначное соответствие между множеством и множеством . Следовательно, имеет мощность континуума.

Кроме того, множества:

и

имеют ту же мощность континуума c, так как отличаются от множества конечным числом точек, что сохраняет их мощность.

Совершенно неожиданный результат получил Г. Кантор, предполагая первоначально, что квадрат со стороной, равной 1, содержит“больше”точек, чем отрезок . Они оказались эквивалентными.

“Я вижу это, но не верю этому”, –сообщал он в письме к Дедекинду.

Действительно, если квадрат расположить в системе координатXOY, как указано ниже нарис. 7.9, то всякой его внутренней точкеW, имеющей координаты

можно поставить в соответствие точку интервала:

Разным точкам W квадрата будут соответствовать разные точки интервала. Можно показать (используя более строгие рассуждения), что такое однозначное соответствие будет взаимно однозначным, поэтому множество точек квадрата со стороной, равной1, и отрезок имеют одинаковую мощность. Более того, не только квадрат, но, например, куб или шар, содержит “столько же” точек, сколько их содержит отрезок .

Сравнение множества натуральных чисел, являющегося счетным, и несчетного множества точек отрезка вызывает вопрос: имеются ли множества промежуточной мощности? Иначе говоря, есть ли бесконечное множество, в котором количество элементов“больше”, чем натуральных чисел, и“меньше”, чем точек на отрезке ? Это есть знаменитаяпроблемаКОНТИНУУМА, которая до сих пор волнует многих математиков. В начале шестидесятых годов

Рис. 7.9. Взаимно однозначное соответствие между точками внутри квадрата и точками интервала .

ХХ-го столетия было установлено, что существуют как системы аксиом, в которых гипотеза континуума истинна, так и аксиоматические построения, в которых она ложна.

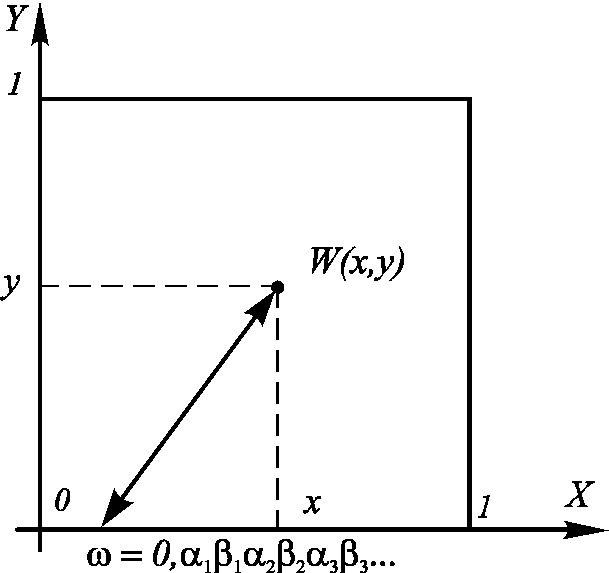
В теории множеств доказаны следующие утверждения:

1. Для любого множества A существует множество большей мощности (см. 2 и 3).

2. Множества самой большой мощности не существует. (см.3).

3. Множество всех подмножеств множества Aимеет мощность большую, чем мощностьA.

4. Множество всех подмножеств счетного множества имеет мощность континуума.

Теория множеств полна проблем и парадоксов, которые и в настоящее время вызывают интерес у исследователей. Один изнихрассмотрен выше. Здесь приведём классическийпарадоксБ. Рассела.

Пусть M – множество всех множеств, а N – множество всех его подмножеств. Тогда мощность множестваNвсех подмножеств должна быть больше мощности множестваM(по утверждению 3). Но по определениюN– подмножество , отсюда,N=M. Получаем неустранимое противоречие.