- •О понятии множества
- •Операции над множествами, их приоритеты
- •Бесконечными множествами.
- •Счетные множества
- •Мощность континуума
- •Числовые множества
- •Аксиомы сложения
- •Аксиомы умножения
- •Аксиомы порядка
- •Аксиома полноты (непрерывности)
- •A c b.
- •Тождества алгебры множеств:
- •Замечание к тождествам 11:
- •Замечания ко всем тождествам с множествами, появляющимся при действиях с ними:
- •Отношения порядка
A c b.
Иррациональное число dрассмотрим в виде:
![]()
Эта бесконечная десятичная дробь будет непериодической, причем, так как
![]()
то a d. Кроме того,
![]()
поэтому d b.
Таким образом, искомое иррациональное число удовлетворяет неравенству
a d b.
Покажем теперь, что точная нижняя грань интервала (0; 1) равна 0:
![]() .
.
Действительно, для всех
![]() справедливо
справедливо
x 0,
следовательно, число 0является нижней границей. Если только
взять любое число![]() ,
то, согласно предыдущему примеру,
найдется такое рациональное
,
то, согласно предыдущему примеру,
найдется такое рациональное![]() ,
что
,
что![]() ,
то есть
,
то есть![]() не может быть нижней границей. (Определение
точной верхней (нижней) грани дано в
разделечисловые
множестванижеаксиомы
полноты.) Следовательно,
не может быть нижней границей. (Определение
точной верхней (нижней) грани дано в
разделечисловые
множестванижеаксиомы
полноты.) Следовательно,![]()
В конце выпишем основные, часто применяемые, результаты теории множеств в виде краткой справки.
МНОЖЕСТВА И ДЕЙСТВИЯ С НИМИ
Замечания:
Понятие множествасчитаютпервоначальнымине определяемым. Поднимпонимают любое собрание, объединение, определенных и отличных друг от друга объектов (нашей интуиции или интеллекта), мыслимое как единое целое.
Создатель теории множеств немецкий математик Георг Кантор (1845–1918) говорил так: “Множество есть многое, мыслимое нами как целое”.
С не достаточно четким понятием множестванужно обращаться осторожно. Рекомендуется рассматривать только такие множества, возможные элементы которых были бы достаточно четко очерченными и неизменными объектами. Например, вряд ли разумно рассматривать множество хороших идей, множество капель воды в стакане и так далее.
Принято считать, что пустое множество, Ø, введено в математике для удобства и единообразия языка и является подмножеством любого множества. Так, если при исследовании множества объектов, обладающих определенным свойством, выясняется, что такие объекты не существуют, то удобно сказать, что “исследуемое множество пусто”, а не объявлять его “несуществующим”.
Очень важны правила приоритета операций с множествами.
Ниже операции с множествами пронумерованы в порядке убывания приоритета, от максимального до наименьшего:
1)
![]() ;
2)
;
2)![]() 3)
3)![]() 4)
4)![]() .
.
Всегда первой выполняется действие в скобках, а при их отсутствии в порядке приоритета, от максимального до наименьшего. Одинаковые операции выполняют последовательно – слева на право.
Замечание:
Действия
![]() и
и![]() с множествамиA
и B
независимые.
с множествамиA
и B
независимые.
Определение:
Множество AΔB=(A\B)![]() (B\A)
– симметрическая разность; она выражается
через независимые операции,
(B\A)
– симметрическая разность; она выражается
через независимые операции,
![]() и
и![]() .
.
Пересечение множеств:
![]() ,
и их дополнения,
,
и их дополнения,
![]() или
или![]() ,
также определяются через независимые
действия (операции),
,
также определяются через независимые
действия (операции),![]() и
и![]() .
.
Универсальное множество U содержит все элементы решаемого типа задач.
Дополнение к
универсальному множеству U
всегда равно пустому множеству,
![]() .В множестве
.В множестве
![]() нет ни одного элемента.
нет ни одного элемента.
Множество
![]() является подмножеством любого множества.
является подмножеством любого множества.
Тождества алгебры множеств:
1*. Законы идемпотентности:
1.1.
![]() 1.2.
1.2.![]()
2*. Коммутативные законы:
2.1.
![]() ;
2.2.
;
2.2.![]() .
.
3*. Ассоциативные законы:
3.1.
![]() ;
;
3.2.
![]() .
.
4*. Дистрибутивные законы:
4.1.
![]() ;
;
4.2.
![]() ;
;
5*. Закон поглощения или восстановления:
5.1.
![]()
5.2.
![]() .
.
6*. Свойства пустого и универсального множеств:
6.1.
![]() 6.2.
6.2.![]() ;
;
6.3.
![]() 6.4.
6.4.![]()
7*. Закон противоречия:
![]() .
.
8*. закон исключения третьего или свойство дополнения:
![]() .
.
9*. Закон инволютивности или закон “двойного отрицания”:
![]() .
.
10*. Законы де Моргана:
10.1.
![]() 10.2.
10.2.![]() .
.
11. Тождества с разностями:
11.1.
![]()
11.2.
![]()
11.3.
![]()
11.4.
![]()
11.5.
![]() – симметрическая разность.
– симметрическая разность.
11.6.
![]() ;
;
11.7.
![]() ;
;
11.8.
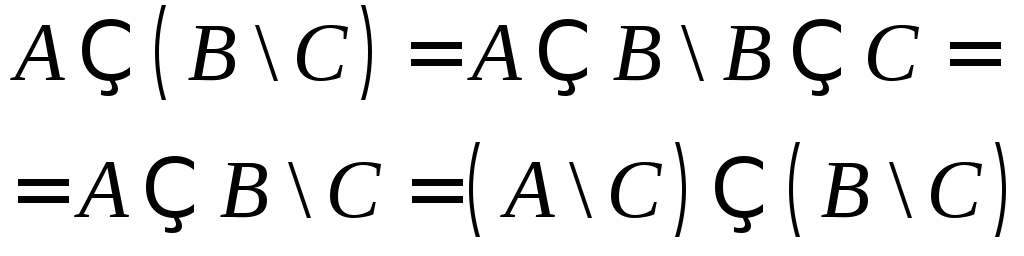 ;
;
11.9.
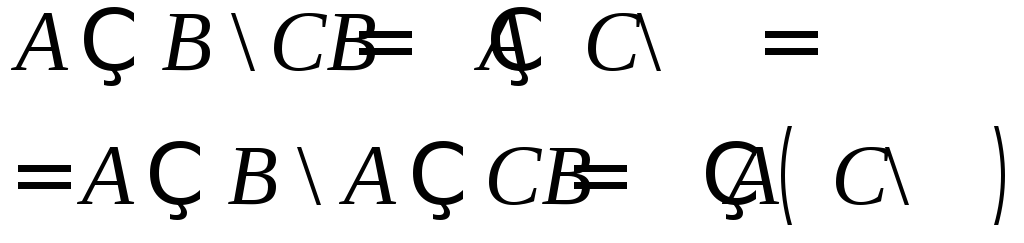 ; здесь учтёно 11.8;
; здесь учтёно 11.8;
11.10
![]() .
.
12. Примеры эквивалентности:
12.1.
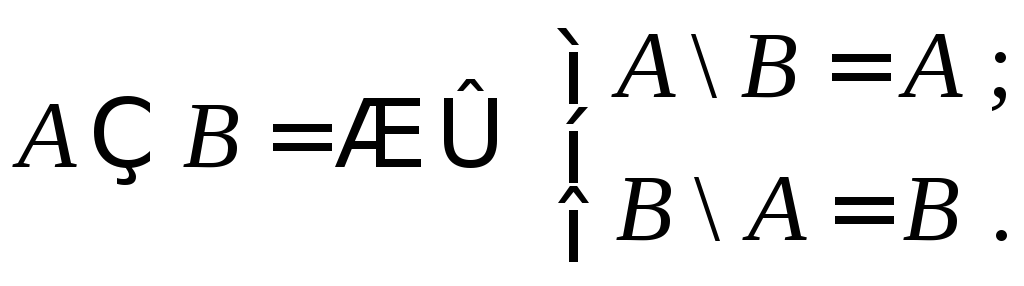
12.2.