
Том-2_РУ
.pdf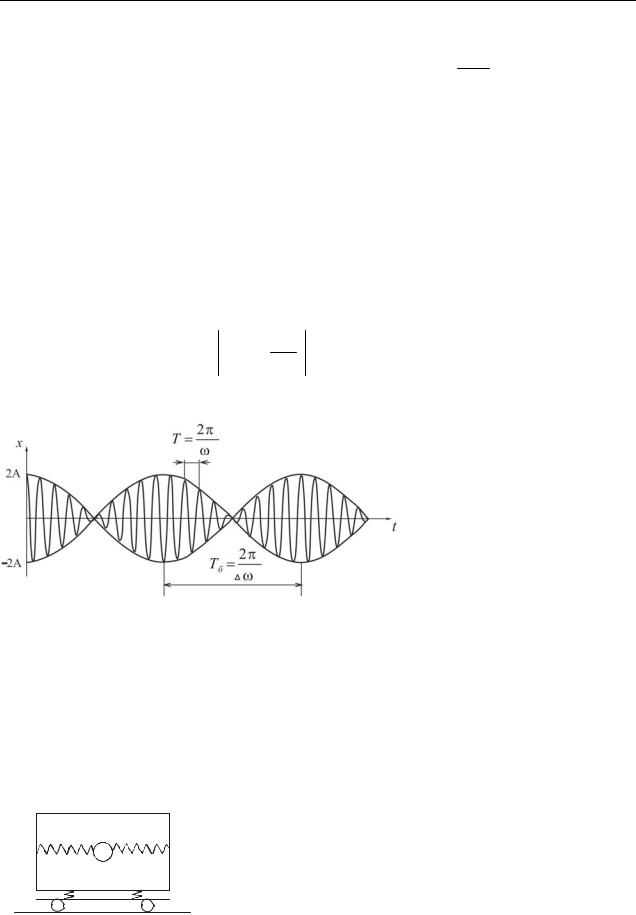
Колебания
Результирующее колебание опишется уравнением
x x1 x2 A cos t cos t 2Acos 2 t cos t
(во втором сомножителе пренебрегаем слагаемым Δω/2 по сравнению с ω). Таким образом, уравнение, описывающее биения, имеет вид:
|
|
|
|
|
||
x |
2Acos |
t |
cos t . |
(5.8) |
||
2 |
||||||
|
|
|
|
|
||
Изменение х будет определяться частотой ω, а выражение под знаком модуля меняется медленно и определяет амплитуду биений. Знак модуля поставили потому, что амплитуда по определению величина положительная.
Таким образом, биения можно рассматривать как почти гармоническое колебание с медленно меняющейся амплитудой. График функции (5.8) дан на
рис. 5.4. Амплитуда A(t) 2Acos 2 t характеризует размах колебаний при би-
ениях. Циклическая частота Δω называется циклической частотой биений. Период биений
T |
|
|
2 |
. |
(5.9) |
|
|
||||
биен |
|
|
|
||
Биения |
используют |
||||
для измерения частоты ко- |
|||||
лебаний путем их сравнения |
|||||
с частотой эталонных коле- |
|||||
баний, |
например, |
при |
|||
настройке музыкальных ин- |
|||||
Рисунок 5.4 |
струментов. |
|
5.3 Сложение взаимно перпендикулярных колебаний |
Сложение взаимно перпендикулярных колебаний можно пронаблюдать |
на примере шарика, закрепленного на пружинах в вагоне (рис. 5.5). Шарик ко- |
леблется на пружинах вдоль направления движения вагона и вместе с вагоном |
колеблется на рессорах перпендикулярно направлению движения. |
Пусть точка совершает гармонические коле- |
бания одной и той же частоты, происходящие |
вдоль координатных осей х и y. Начало отсчета вы- |
берем так, чтобы начальная фаза первого колеба- |
ния была равна нулю. Тогда уравнения колебаний |
запишутся следующим образом: |
Рисунок 5.5 |
x A1 cos t |
|
|
|
y A |
cos t , |
(5.10) |
|
2 |
|
|
21
Колебания
где 02 01 – разность фаз складываемых колебаний. Эти два уравнения
составляют систему, которая задает траекторию движения в параметрической форме. Чтобы получить уравнение траектории в обычной форме, исключим из (5.10) параметр t. Из первого уравнения
|
cos t |
x |
, |
|
|
(5.11) |
|||
|
A |
|
|
||||||
|
|
|
|
|
|
|
|
||
следовательно |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
x |
2 |
|
|
sin t |
1 cos |
t |
|
|
|
(5.12) |
|||
|
|
||||||||
|
1 A |
. |
|||||||
|
|
|
|
|
|
1 |
|
|
|
Из второго уравнения системы (5.10) по формуле косинуса суммы имеем:
|
y |
cos t cos t cos sin t sin . |
(5.13) |
|||||||||
|
A |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
В выражение (5.13) подставим вместо |
sin t |
и cos t |
их значения по |
|||||||||
формулам (5.11) и (5.12). В результате получим: |
|
|
|
|
|
|||||||
|
|
|
y |
|
x |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
A |
A cos 1 |
|
A |
sin . |
(5.14) |
||||
|
|
|
|
|
||||||||
|
|
2 |
1 |
|
|
|
1 |
|
|
|
||
После математических преобразований это уравнение можно привести к виду (попробуйте выполнить это самостоятельно):
|
y |
|
A1 |
|
A 2 |
A 1 |
x |
|
|
A2 |
|
|
Рисунок 5.6 |
y |
A1 |
A2 |
A1 |
x |
A 2 |
Рисунок 5.7 |
x2 |
|
y2 |
|
2xy |
cos sin2 . |
(5.15) |
A2 |
A2 |
|
||||
|
|
A1 A2 |
|
|||
1 |
|
2 |
|
|
|
|
Из аналитической геометрии известно, что уравнение (5.15) представляет собой уравнение эллипса, оси которого ориентированы относительно координатных осей x и y произвольно.
Рассмотрим некоторые частные случаи.
1. Разность фаз складываемых колебаний
0 .
Вэтом случае уравнение (5.15) примет вид
|
x |
|
y |
2 |
|
|
|
|
|
0. |
|||
A |
A |
|||||
|
|
|||||
|
1 |
|
2 |
|
|
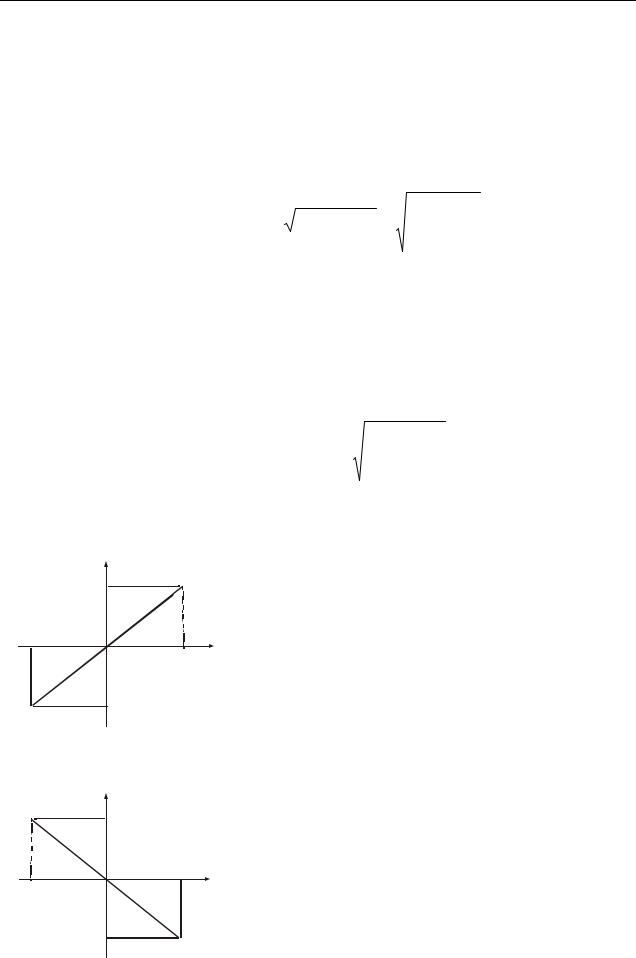
Из него получается уравнение прямой, проходящей через начало координат и лежащей в I и III четвертях (рис. 5.6)
22
|
|
|
Колебания |
|
|
y |
A2 |
x . |
(5.16) |
||
A |
|||||
|
|
|
|
||
|
1 |
|
|
|
|
2. Разность фаз складываемых колебаний . Уравнение (5.15) примет вид:
|
x |
|
y |
2 |
|
|
|
|
|
0. |
|||
A |
A |
|||||
|
|
|||||
|
1 |
|
2 |
|
|
Из него получается уравнение прямой, проходящей начало координат и лежащей в II и IV четвертях (рис. 5.7):
y |
A2 |
x . |
(5.17) |
|
A |
||||
|
|
|
||
1 |
|
|
||
3. Разность фаз складываемых колебаний 2 . Уравнение (5.15) переходит в следующее:
x2 |
|
y2 |
1, |
(5.18) |
|
A2 |
A2 |
||||
|
|
|
|||
1 |
|
2 |
|
|
то есть в каноническое уравнение эллипса. Полуоси эллипса равны соответствующим амплитудам. Если A1 A2 R , то эллипс вырождается в окружность
x2 y2 R2 . |
(5.19) |
Случаи =π/2 и =Δφ π/2 отличаются направлением движения по эллипсу или окружности (рис. 5.8).
y
A2
2
Если точка одновременно колеблется в A1 двух взаимно-перпендикулярных направлениях так, что частоты относятся как целые числа (т.е. частоты кратные), то она будет двигаться вдоль замкнутой кривой, форма которой зависит от отношения амплитуд A2 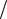 A1 ,
A1 ,
кратности частот 2  1 и разности начальных фаз .
1 и разности начальных фаз .
A2
Рисунок 5.8
A1 x
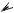
2
Такие замкнутые траектории точки, одновременно совершающей гармонические колебания в двух взаимно перпендикулярных направлениях, называются фигурами Лиссажу*. Фигуры Лиссажу вписываются в прямоугольник, стороны которого параллельны осям координат 0x и 0y и равны соответственно
2А1 и 2А2.
________________________________________________________________________________________________________________________
*Лиссажу Жан Энтуан (1822–1880), французский физик.
23
Колебания
Отношение частот y 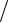 x равно отношению числа касаний фигуры Лиссажу с
x равно отношению числа касаний фигуры Лиссажу с
горизонтальными и вертикальными сторонами прямоугольника, в который она вписана.
A *
1
y
A 2
*
A2
1 2
2
Рисунок 5.9
|
|
y |
|
n |
x |
. |
(5.20) |
|
|
x |
|
|
|||
|
|
|
ny |
|
|||
|
Пример: |
|
|
|
|
|
|
A1 x |
Число касаний фигуры с горизонтальными |
||||||
сторонами: nx=4, число касаний с вертикальными сторонами: ny=2 (рис. 5.9). Отношение частот
y 4 2x 2
С помощью фигур Лиссажу можно найти неизвестную частоту по известной.
§6 Затухающие колебания
Вреальных физических системах, участвующих в колебательном движении, всегда присутствуют силы сопротивления (внутреннее трение, сопротивление среды, потери энергии за счет нагревания проводников и т. д.), действие которых уменьшает энергию системы. Уменьшение энергии приводит к затуханию колебаний.
6.1Затухающие колебания пружинного маятника
Вреальных условиях на шарик массы m, совершающий колебания вдоль оси 0x под действием силы упругости, действует также сила сопротивления. Предположим, что это сила вязкого трения. При малых скоростях она пропорциональна скорости
F r v r dx , |
(6.1) |
c |
dt |
|
где r – коэффициент сопротивления. Знак « » обусловлен тем, что сила и скорость имеют противоположные направления. В этом случае второй закон Ньютона запишется в виде
kx r |
dx |
m |
d 2 x |
. |
(6.2) |
|
dt |
dt 2 |
|||||
|
|
|
|
Разделив обе части полученного уравнения на m, перепишем его следующим образом:
d 2 x |
|
r dx |
|
k |
x 0 |
(6.2а) |
||
|
|
|
|
|||||
dt 2 |
m dt |
m |
||||||
|
|
|
|
|||||
24
|
|
|
|
|
|
|
|
Колебания |
|
или |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
(6.3) |
||
где обозначено: |
|
x |
2 x 0 x 0 , |
||||||
r |
|
|
|
|
k |
|
|
|
|
|
, |
|
02 |
|
. |
|
|
||
2m |
|
|
|
|
|||||
|
|
|
|
|
m |
|
|
||
Величину β называют коэффициентом затухания. Напомним, что ω0 – собственная частота колебаний, то есть частота, с которой совершались бы свободные колебания при отсутствии трения.
Уравнение (6.3) называют дифференциальным уравнением затухающих колебаний. Решение уравнения (6.3) зависит от соотношения между коэффициентом затухания β и собственной частотой ω0. Если затухание невелико (β<ω0), то его решение имеет вид:
x t A e t cos t |
0 |
, |
(6.4) |
||
|
0 |
|
|
|
|
где |
02 |
2 , |
|
|
(6.5) |
– частота затухающих колебаний. Согласно (6.4) движение маятника мож-
но рассматривать как колебание с частотой ω и амплитудой А, изменяющейся по закону
|
|
|
|
|
|
|
|
|
|
|
|
A A t A e t . |
(6.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Рисунок 6.1 |
График функции x(t) дан на рисунке 6.1. |
||||||||
|
|
|
|
|
|
6.2 Затухающие колебания в колебательном контуре |
|||||||||
|
|
|
|
Всякий реальный контур (рис. 6.2) обладает активным сопротивлением |
|||||||||||
(R 0). Энергия, |
запасенная в контуре, расходуется в этом сопротивлении на |
||||||||||||||
|
|
|
|
|
R |
нагревание, поэтому свободные колебания затухают. |
|||||||||
|
|
|
|
|
Получим дифференциальное уравнение затухающих |
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
колебаний, используя закон сохранения энергии. Потери |
|||||||
|
|
|
|
|
|
|
|
||||||||
C |
|
|
|
|
|
|
L |
энергии равны количеству тепла, |
выделившемуся на ак- |
||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
тивном сопротивлении: |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
d Wэл Wм Q . |
|
(6.7) |
||
|
Рисунок 6.2 |
|
|
|
|
||||||||||
|
Знак « |
» перед дифференциалом означает, что энергия |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
уменьшается. |
|
|
|
|
|
|
|
Согласно (3.19) и (3.20): |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
W |
|
q2 |
|
W |
LI |
2 |
|
|
|
|
|
|
|
|
|
|
, |
|
. |
|||
|
|
|
|
|
|
|
|
|
2C |
2 |
|||||
|
|
|
|
|
|
|
|
|
эл |
|
|
м |
|
||
По закону Джоуля Ленца
25

Колебания
|
|
Q I 2 Rdt . |
|
|
(6.8) |
|||
Записанные соотношения подставим в (6.7) и найдем дифференциал: |
|
|||||||
|
1 |
|
L |
|
|
I 2 Rdt |
|
|
|
|
2qdq |
|
2IdI |
(6.9) |
|||
2C |
2 |
|||||||
|
|
|
|
|
|
|||
Разделив (6.9) на произведение Ldt и учтя, что
I |
dq |
, |
dI |
|
d 2q |
, |
|
dt |
dt |
dt 2 |
|||||
|
|
|
|
получим дифференциальное уравнение второго порядка:
|
|
d |
2q |
|
R dq |
|
1 |
|
q 0 |
||
или |
|
dt 2 |
L dt |
|
LC |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
||||
где |
|
q |
2 q 0q |
||||||||
R |
|
|
|
|
|
|
|
|
1 |
|
|
|
, |
|
|
|
02 |
|
|
. |
|||
2L |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
LC |
|||
(6.10)
(6.11)
Уравнение (6.11) по своему виду совпадает с дифференциальным уравнением (6.3) для затухающих механических колебаний. Если затухание невелико ( 0 ), то его решение имеет вид:
|
q(t) q0e t cos t 0 , |
(6.12) |
где |
02 2 частота затухающих колебаний. |
(6.13) |
График функции q(t) имеет тот же вид, что и x(t) (см. рис. 6.1).
6.3 Основные характеристики затухающих колебаний
Величинами, характеризующими затухающие колебания, являются:
1. Коэффициент затухания (β) – скалярная физическая величина, характеризующая скорость затухания.
[β]=1/с
Для механических колебаний |
|
||||
|
r |
. |
(6.14) |
|
|
|
|
|
|||
|
2m |
|
|
||
Для электромагнитных колебаний |
|
||||
|
R |
. |
(6.15) |
|
|
|
Рисунок 6.3 |
||||
|
2L |
|
|||
Чем больше коэффициент затухания, тем быстрее уменьшается амплитуда (рис. 6.3).
26

Колебания
2. Время релаксации (τ) – время, в течение которого амплитуда колебаний уменьшается в е =2,71… раз (е – основание натуральных логарифмов).
Найдем связь между β и τ. Амплитуда затухающих колебаний уменьшается согласно (6.6) по закону
A(t) A0e t
Если t , то A( ) Ae0 . Сделаем подстановку:
Ae0 A0e .
Отсюда 1.
|
1 |
(6.16) |
|
|
|
3. Логарифмический декремент затухания (λ) – безразмерная величина,
количественная характеристика быстроты затухания колебаний, численно равная натуральному логарифму отношения двух следующих друг за другом амплитуд A(t) и A(t T ) в одну и ту же сторону (см. рис. 6.1)
ln |
A(t) |
(6.17) |
A(t T ) |
Установим связь между логарифмическим декрементом затухания и коэффициентом затухания.
Ae t
ln A0e0 (t T ) ln e T T .
T . |
(6.18) |
Средние значения логарифмических декрементов некоторых систем приведены в таблице 6.1.
4. Число колебаний за время релаксации – Ne.
Ne |
|
|
1 |
|
1 . |
(6.19) |
|
T |
T |
||||||
|
|
|
|
|
5. Добротность колебательной системы (Q) – безразмерная физическая величина, характеризующая убыль энергии за период и равная произведению 2π на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за один период Т.
Q 2 W (t) |
, |
(6.20) |
W |
|
|
T |
|
|
где WT W (t) W (t T ) .
27

Колебания
Если затухание невелико, то добротность определяется по соотношению:
Q |
. |
(6.21) |
|
|
|
Большим значениям Q соответствует слабое затухание.
Типичные значения добротности некоторых систем приведены в таблице 6.1.
Таблица 6.1. Средние значения логарифмических декрементов затухания и типичные значения добротности Q некоторых систем
Колебательная система |
Декремент затухания, |
Добротность, Q |
Радиоконтуры обычные |
0,02 0,05 |
10 100 |
Камертон |
0,001 |
100 |
Кварцевая пластинка |
10 10 |
2·10 |
СВЧ резонаторы |
10 10 |
10 10 |
Оптический резонатор |
10 10 |
10 10 |
Сейсмические волны |
|
25 1400 |
Струна (скрипка, рояль) |
|
1000 |
6. Энергия колебаний. Так как энергия колебаний пропорциональна квадрату амплитуды (см. формулу (4.4)), то закон изменения энергии при затухающих колебаниях примет вид:
W (t) W e 2 t |
, |
(6.22) |
||
где в соответствии с (4.4): |
0 |
|
|
|
kA2 |
|
|
||
W |
|
(6.23) |
||
|
0 . |
|||
0 |
2 |
|
|
|
|
|
|
||
6.4 Апериодический процесс
Рассмотрим, каким будет характер движения при больших коэффициентах затухания. Согласно (6.5) частота затухающих колебаний
02 2 , |
T |
2 |
. |
|
|||
|
|
|
|
Если 0 , то частота затухающих колебаний обращается в нуль, а пе-
риод – в бесконечность, то есть движение перестает быть периодическим. Если 0 , то движение носит апериодический (непериодический) ха-
рактер. Это означает, что выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
На рис. 6.4 показаны графики изменения координаты при апериодическом процессе в зависимости от начальных условий.
1 – направление отклонения и направление начальной скорости совпадают;
28

Колебания
2 – направление отклонения и направление начальной скорости противоположны, но скорость маленькая; 3 – направление отклонения и направление начальной скорости противоположны.
x
1
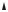 2 x0
2 x0
3
Рисунок 6.4
Таким образом, при 0 ко-
лебательная система переходит к апериодическому процессу.
На практике нередко возникает задача погашения колебаний в момент их возникновения (например, колебания стрелки измерительного
tприбора, колебаний кузова автомобиля). Устройства, которые позволяют увеличить затухание колебательной системы, называются демпферами
или амортизаторами.
§7 Вынужденные колебания
Чтобы вызвать вынужденные колебания нужно оказывать на систему внешнее периодически изменяющееся воздействие.
7.1Вынужденные механические колебания
Вкачестве колебательной системы рассмотрим пружинный маятник, совершающий колебания вдоль оси 0x (см. п. 3.1). Переменная внешняя сила, приложенная к системе и вызывающая ее механические колебания, называется вынуждающей силой. Пусть вынуждающая сила изменяется по закону
F(t) F0 cos t , |
(7.1) |
где Ω – частота вынуждающей силы, а F0 – ее амплитудное значение. Кроме вынуждающей силы на маятник действуют также те силы, что и при свободных колебаниях, то есть квазиупругая сила и сила сопротивления (см. п. 6.1). Запишем второй закон Ньютона:
kx r |
dx |
F |
cos t m |
d 2 x |
. |
|
|
||||
|
dt |
0 |
|
dt2 |
|
|
|
|
|
Разделив это уравнение на m, перепишем его в виде:
|
d |
2 x |
|
|
r dx |
|
k |
|
F |
|
||
|
|
|
|
|
|
|
|
|
|
x |
0 |
cos t , |
|
dt2 |
|
m dt |
|
m |
|||||||
|
|
|
|
|
|
m |
|
|||||
или |
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
x |
2 x 0 x f0 cos t , |
||||||||||
(7.2)
(7.3)
29
Колебания |
|
|
|
|
|
|
|
|
|
|
|
где |
|
f0 F0 , |
r , |
|
|
|
02 k . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
2m |
|
|
|
|
m |
|
|
|
|
Уравнение (7.3) является дифференциальным уравнением вынужденных |
||||||||||
механических колебаний. Из теории дифференциальных уравнений известно, |
|||||||||||
что общее решение данного неоднородного дифференциального уравнения |
|||||||||||
равно сумме общего решения соответствующего однородного уравнения и |
|||||||||||
частного решения неоднородного: |
|
|
|
|
|
|
|
|
|||
|
|
|
x(t) x1(t) x2 (t) . |
|
|
|
|
|
|
|
|
|
Общее решение однородного уравнения уже известно (см. формулу (6.4)): |
||||||||||
|
|
x |
t A e t cos t |
0 |
. |
|
|
|
|
||
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
Можно показать, что частное решение, удовлетворяющее правой части |
||||||||||
уравнения (7.2), имеет вид: |
|
|
|
|
|
|
|
|
|
||
|
|
|
x2 t Acos t . |
|
|
|
|
|
|
||
|
Амплитудное значение x (t) , равное A e t , после начала вынужденных |
||||||||||
|
|
|
1 |
0 |
|
|
|
|
|
|
|
колебаний более или менее быстро уменьшается. Следовательно, через некото- |
|||||||||||
|
|
x Acos( t 0) |
рое время τ после начала колеба- |
||||||||
|
t |
ний свободные колебания маятни- |
|||||||||
|
|
|
ка |
практически |
прекращаются: |
||||||
x |
e |
|
|
||||||||
|
|
x(t) x2 (t) . Маятник переходит в |
|||||||||
|
|
|
|
||||||||
|
|
|
|
состояние |
установившихся |
вы- |
|||||
|
|
|
|
нужденных |
колебаний, |
которые |
|||||
|
|
|
t |
совершаются с частотой |
вынуж- |
||||||
|
|
|
дающей силы (см. рис. 7.1): |
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x t Acos t , |
|
(7.4) |
||
|
переходный |
установившиеся |
где φ представляет собой вели- |
||||||||
|
процесс |
колебания |
|
чину отставания по фазе вынуж- |
|||||||
|
Рисунок 7.1 |
|
денного колебания от обусловив- |
||||||||
|
|
|
|
шей его вынуждающей силы. Ам- |
|||||||
плитуда этих колебаний А и значение φ определяются как параметрами систе- |
|||||||||||
мы (m, 0), так и параметрами вынуждающей силы (F0, ). |
|
|
|
||||||||
A |
|
|
F0 |
|
. |
(7.5) |
|
m |
02 2 |
2 4 2 2 |
|||||
|
|
tg |
2 |
. |
|
(7.6) |
|
|
|
2 |
2 |
|
|||
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
30
