1.5. Общий случай линейной алгебраической системы уравнений. Условие совместности Ранг матрицы

Определитель k-го порядка, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы А, называется минором k-го порядка, порожденным данной матрицей.

Например, для матрицы А

минор второго порядка можно получить, выбрав 1 и 3 строки, а также 1-й и 4-й столбцы: 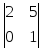.Очевидно, что минорами, порожденными этой матрицей, являются и другие определители 2-го порядка:

и т.д.

Данная матрица имеет минорами и определители 3-го порядка

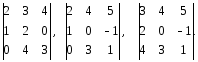
Рангом матрицы А (обозначается ) называется наивысший порядок отличных от нуля миноров, порожденных этой матрицей.

В рассматриваемой матрице А наивысший порядок ее миноров равен трем. Вычислим один из них.

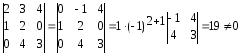
Так как этот минор отличен 0, то .

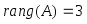Вычислять все миноры, порождаемые данной матрицей, затруднительно. Поэтому для определения ранга матрицы можно использовать метод приведения матрицы к ступенчатому виду с помощью элементарных преобразований.

Элементарными преобразованиями матрицы называются:

1) умножение какой-либо строки (столбца) на число ,

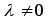2) перестановка двух строк (столбцов),

3) прибавление к элементам одной строки (столбца) соответственных элементов другой строки (столбца), умноженных на одно и то же число .

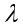Элементарные преобразования не меняют ранг матрицы.

Две матрицы называются эквивалентными, если одна из них получена из другой при помощи элементарных преобразований. Эквивалентные матрицы имеют один и тот же ранг.

С помощью эквивалентных преобразований матрицу можно привести к ступенчатому виду.

Матрица называется ступенчатой, если в ее первой строке имеется хотя бы один элемент отличный от 0, а в каждой последующей строке первый отличный от 0 элемент стоит правее первого отличного от 0 элемента предыдущей строки. Например,

.

Ранг ступенчатой матрицы равен числу ее ненулевых строк. Для определения ранга матрицы нужно, применяя элементарные преобразования, привести ее к ступенчатому виду.

Исследование на совместность систем линейных алгебраических уравнений

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными x₁, x₂, …, x_n:

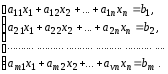
Составим две матрицы:

и ,

где А − основная матрица системы, В − расширенная матрица системы.

Условие совместности любой линейной алгебраической системы определяется теоремой Кронекера-Капелли: для того, чтобы линейная алгебраическая система уравнений была совместна необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы системы, т. е. .

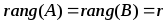При этом возможны два случая:

а) 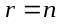, тогда система имеет единственное решение;

б) 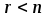, тогда система имеет бесконечное множество решений (при этомr неизвестных являются основными, остальные n - r неизвестных – свободными, им можно придавать произвольные значения, в зависимости от которых принимают значения основные переменные).

1.6. Метод Гаусса решения систем линейных алгебраических уравнений

Основная идея метода Гаусса − последовательное исключение неизвестных.

Решение системы линейных алгебраических уравнений методом Гаусса состоит из двух этапов.

На первом этапе (прямой ход) система приводится к ступенчатому виду.

На втором этапе (обратный ход) идет последовательное определение неизвестных из ступенчатой системы.

На практике удобнее работать не с системой, а с ее расширенной матрицей, выполняя элементарные преобразования над ее строками.

Сущность метода проиллюстрируем на примере решения системы из трех уравнений с тремя неизвестными.

Таким образом, если число уравнений в полученной ступенчатой системе равно числу неизвестных, то система имеет единственное решение. Все неизвестные в этом случае определяются последовательно, начиная с последнего.

Если же число уравнений в ступенчатой системе меньше числа неизвестных (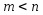), то система имеетбесконечное множество решений. В этом случае неизвестные x₁, x₂,…, x_n могут быть выражены через остальные неизвестные.

Система не имеет решений, если одно из уравнений имеет отличный от нуля свободный член, а все коэффициенты в левой части равны нулю, т. е. если при преобразованиях получаются уравнения вида

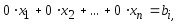где .

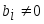Этому случаю соответствует появление в ступенчатой матрице строки вида

.

23