Лабораторная работа №1.

Тема: Организация программ по обработке массивов и матриц.

Цель работы: закрепление теоретического материала, освоение методов разработки алгоритмов и приобретение практических навыков в программной реализации задач обработки многомерных массивов.

Требования к выполнению работы:

В каждом из вариантов заданий по лабораторной работе необходимо составить алгоритм и программу, которые предусматривают следующие функции:

- формирование элементов исходной матрицы одним из способов:

а) случайным образом; б) вводом с клавиатуры; в) чтением из файла;

- печать матрицы (исходной и преобразованной);

- обработку матрицы в соответствии с условием задачи;

Программа должна иметь как минимум три вышеперечисленные функции. Функции должны быть организованы так, чтобы выполнять обработку матриц любой размерности. Категорически запрещается использовать глобальные переменные. Обработка матрицы должна быть реализована двумя способами:

а) типизированной функцией;

б) фукнцией неопределенного типа.

Группа а

Варианты заданий.

1. Для прямоугольной матрицы определить среднее арифметическое значения S ее элементов, a также процент элементов матрицы, превышающих это значение.

2. Рассматривая каждую строку прямоугольной матрицы как вектор, найти максимальное скалярное произведение S.

3. В прямоугольной матрице найти номера столбцов, содержащих соответственно максимальное и минимальное количество отрицательных элементов.

4. Рассматривая каждый столбец прямоугольной матрицы как вектор, определить номер вектора-столбца, длина L которого максимальна:

5. Рассматривая элементы строки прямоугольной матрицы координатами точек в n-мерном пространстве, определить максильное расстояние d между точками.

6. В квадратной матрице найти значение максимального элемента, который в наименьшей степени отличается от среднего арифметического зна­чения элементов данной матрицы.

7. В квадратной матрице найти значение максимального элемента среди элементов, распо­ложенных выше главной диагонали, и минимального элемента среди элементов, расположенных ниже глав­ной диагонали.

8. В прямоугольной матрице определить номера строк, сумма модулей элементов которых наибольшая и наи­меньшая по сравнению с другими строками.

9. В прямоугольной матрице определить среднее арифме­тическое значение S и дисперсию D отдельно для поло­жительных и отдельно для отрицательных элементов данной матрицы (нулевые элементы при расчете S и D не учитывать):

10. В прямоугольной матрице каждый столбец содержит компоненты вектора в n-мерном пространстве. Определить минимальный угол между векторами.

Р. S. Для векторов:

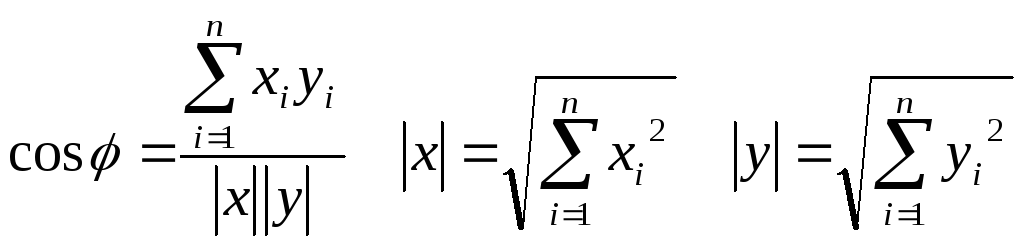
11. Для каждого столбца прямоугольной матрицы вычис­лить среднее геометрическое Р модулей его элементов. (матрица не должна иметь нулевых элементов):

12. В каждом столбце квадратной матрицы найти макси­мальный по модулю элемент и, если он не является диагональным, поменять его местами с диагональным элементом, подсчитать количество таких перестановок.

13. В прямоугольной матрице все элементы положитель­ные числа. Определить для каждого столбца матрицы гармоническое среднее S и определить номер столбца, имеющего максимальное значение S.

P.S. Для массива A (a₁,a₂,…,a_n)

14. К каждому элементу главной диагонали квадратной матрицы прибавить такое значение, чтобы сумма элемен­тов в соответствующем столбце матрицы была нуле­вой.

15. В прямоугольной матрице определить количество столбцов, полностью состоящих из положительных элементов.

Р.S. Последовательный просмотр элементов столбца ор­ганизовать таким образом, чтобы при обнаружении первого отрицательного элемента остальные элементы столбца не проверялись.

16. Для каждого столбца прямоугольной матрицы подсчи­тать сумму входящих в него элементов и определить, имеются ли столбцы с одинаковой суммой. Подсчитать количество таких пар столбцов.

17. Рассматривая каждый столбец прямоугольной матри­цы как вектор определить имеются ли в матрице орто­гональные вектор-столбцы. Подсчитать количество пар таких столбцов.

P.S. Векторы называют ортогональными, если их скалярное произведение равно нулю.

18. В прямоугольной матрице определить количество строк, элементы которых полностью упорядочены по возрастанию.

19. В прямоугольной матрице, имеющей четное количест­во строк, переставить каждую пару строк (1,2),(3,4),... та­ким образом, чтобы первой была строка с меньшей суммой элементов.

20. В прямоугольной матрице определить количество столбцов, содержащих элементы только одного знака (положительные или отрицательные) и не содержащих нулевых элементов.

21. Каждая строка прямоугольной матрицы определяет координаты точек в n-мерном пространстве. Точки при­надлежат ломаной линии, начинающейся с точки, со­держащей в первой строке, и заканчивающейся в точке, содержащейся в последней строке матрицы. Вычислить длину ломаной и определить номер ее отрезка, имею­щего наибольшую длину.

22. Каждую строку прямоугольной матрицы сгладить по формуле:

a_ij=(a_ij-1+a_ij+a_ij+1)/3 для каждой строки определить максимальное отклоне­ние d ее элементов от среднего арифметического значе­ния данной строки до и после сглаживания.

23. В каждом столбце прямоугольной матрицы подсчитать количество положительных элементов, окруженных слева и справа по крайней мере одним отрицательным элемен­том. Первый и последний элементы строки не учиты­вать. Определить номер строки, имеющей максималь­ное количество таких элементов.

24. В каждом столбце прямоугольной матрицы найти ми­нимальный элемент и определить номер столбца, имеющего максимальное значение такого элемента.

25. Определить, имеются ли в прямоугольной матрице линейно зависимые строки и подсчитать количество пар таких строк.

P.S. Строки i и m линейно зависимы, если