1.2. Друга інтерполяційна формула Ньютона

Використовуючи другу інтерполяційну формулу Ньютона, перша похідна функції може бути обчислена так:

. (8)

Для диференціювання в вузлових точках формула (8) прийме вид:

. (9)

Другу похідну можна обчислити з виразу

. (10)

Приклад 2. Обчислити першу та другу похідні функції в точці. Функція задана на відрізкув рівновіддалених вузлах,.

Зауважимо, що крок розрахунків, таблиця значень функції та таблиця кінцевих різностей будуть ті самі, як і обчислені в прикладі 1, але для розрахунків використаємо формули (8) та (10). Обчислення будемо проводити з чотирма знаками після коми. Коефіцієнти при занесемо в таблицю:

Таблиця 5 – Коефіцієнти другої формули Ньютона

	Коефіцієнт	Значення
		-0,4349
для першої похідної		0,0651
		-0,0070
		-0,0205
для 2-ї похід­ної		0,5651
		0,3589

Отримаємо:

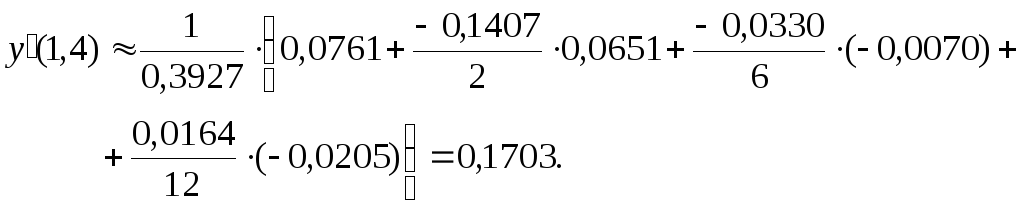
Точне значення . Похибка обчислень складає:

.

Обчислимо другу похідну функції .

Точне значення . Похибка обчислень складає:

.

■

1.3. Формула Ньютона для не рівновіддалених вузлів інтерполяції

Формула Ньютона для не рівновіддалених вузлів інтерполяції має вид:

(11)

Тут , – розподілені різниці-го порядку

Позначимо,

.

Диференціюючи обидві частини рівності (11) один раз, отримаємо:

(12)

Друга похідна функції за формулою Ньютона:

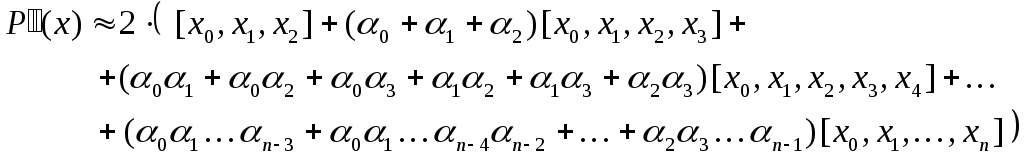(13)

Для диференціювання в вузлах інтерполювання формули (12) – (13) спрощуються, оскільки при відповідне значення. Так, наприклад, для, маємо:

(14)

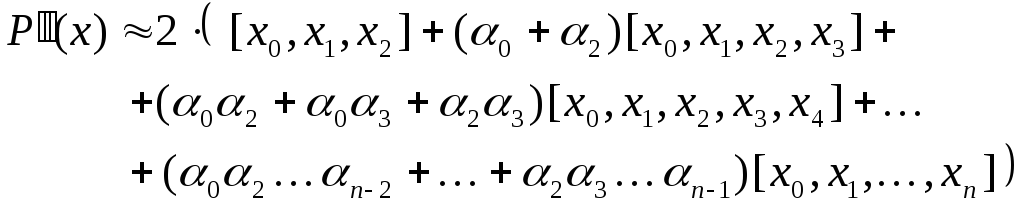(15)

Приклад 3. Знайти першу та другу похідні функції в точці, якщо функція задана таблицею:

Таблиця 6 – Таблиця значень функції

в не рівновіддалених вузлах

№
0	0	0
1	0,628	0,588
2	0,785	0,707
3	1,047	0,866
4	1,571	1

Складемо таблицю розподілених різностей:

0	0
		0,935
0,628	0,588		-0,224
		0,760		-0,134
0,785	0,707		-0,364		0,029
		0,607		-0,088
1,047	0,866		-0,447
		0,256
1,571	1

Обчислимо першу та другу похідні функції .

Знайдемо :

	0	0,628	0,785	1,047	1,571
	0,393	-0,236	-0,393	-0,654	-1,178

Оскільки

,

отже,

.

Точне значення . При цьому похибка складає

.

Для другої похідної

Відповідне значення

.

Точне значення . Похибка складає

.

Обчислимо за допомогою формули Ньютона для не рівновіддалених вузлів значення першої та другої похідної в вузлі . В цьому випадкуі формули для обчислення похідних спрощуються:

,

.

Тут .

	0	0,628	0,785	1,047	1,571
	0,628	0	-0,157	-0,419	-0,942

Звідки отримаємо

.

Точне значення і похибка:

, .

Друга похідна в вузлі:

.

Точне значення і похибка:

, .

■